Приведение пространственной системы сил

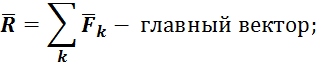
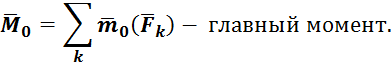
Замечания.

1. Сила не является здесь равнодействующей, так как заменяет систему сил не одна, а с появившейся парой сил, имеющей момент .

2. Значение от выбора центра не зависит, а значение меняется с изменением центра , в который переносятся силы.

11. ПРИВЕДЕНИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ,

НЕ НАХОДЯЩЕЙСЯ В РАВНОВЕСИИ,

К ПРОСТЕЙШЕМУ ВИДУ

Результат приведения зависит от значений и направлений главного вектора и главного момента .

Случай 1: .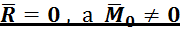

Система сил приводится к паре сил с моментом . Значение от выбора центра не зависит. Это значение вычисляется по составляющим его проекциям

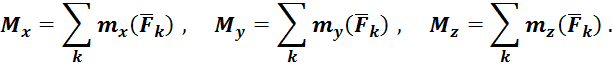
Случай 2: .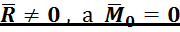

Система сил приводится к равнодействующей , приложенной в центре . Значение вычисляется по составляющим её проекциям

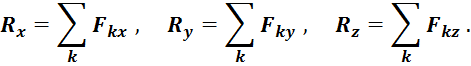
Случай 3: .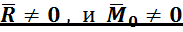

Система сил приводится к равнодействующей , но (!) не приложенной в центре .

В этом случае может быть три варианта (3.1, 3.2 и 3.3).

Вариант 3.1: 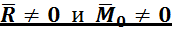, причём перпендикулярен .

Система сил приводится к силе и паре сил и , лежащих в той же плоскости, что и , и создающих момент (рис. 26).

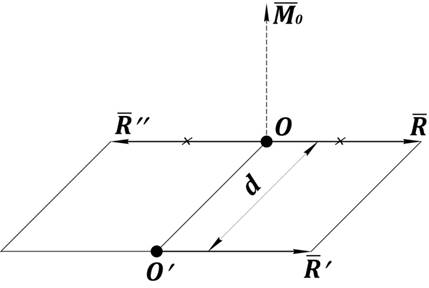
Рис. 26. Приведение пространственной системы сил

к простейшему виду:

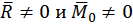, причём перпендикулярен

Можно принять 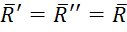. Тогда силы уравновесятся ().

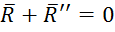Система сил приводится к одной равнодействующей 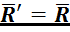, приложенной в точке . Расстояние от точки до точки определяется из выражения

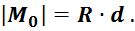
Вариант 3.2: 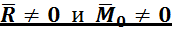, причём параллелен .

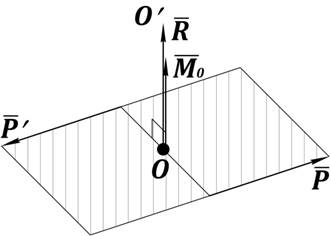
Рис. 27. Приведение пространственной системы сил

к простейшему виду:

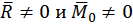, причём параллелен

– момент от пары сил и (рис. 27).