Прямая и обратная задачи электростатики

3.  По шару радиуса равномерно распределен заряд с плотностью . Рассчитайте потенциал электрического поля данного шара.

4.  По поверхности сферы радиуса равномерно распределен заряд с плотностью . Рассчитайте потенциал электрического поля данной сферы.

5.  Заряд равномерно распределен по объему шара радиуса . Найдите потенциал электрического поля внутри и вне шара.

6.  Бесконечно длинный цилиндр радиуса равномерно заряжен по поверхности с плотностью . Определите потенциал электрического поля цилиндра.

7.  Дан диполь . Показать, что напряженность электрического поля, создаваемого диполем, можно рассчитать по формуле .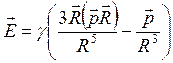

Дополнительный блок задач

8.  Тонкое круглое кольцо радиуса состоит из двух равномерно и противоположно заряженных полуколец с линейными плотностями заряда и . Найдите потенциал электрического поля на оси кольца.

9.  Дан диск радиуса , равномерно заряженный по поверхности с плотностью заряда . В центре диска восстановлен перпендикуляр. На расстоянии от диска на перпендикуляре находится точка наблюдения . Найдите потенциал электрического поля в этой точке.

10.Точечный заряд находится в центре окружности. Вычислить работу по переносу пробного заряда из одного конца диаметра в другой по дуге окружности. Выполните задание двумя способами: учитывая симметрию задачи (по формуле работы) и опираясь на определение потенциала.

11.Выполните решение предыдущего упражнения для перемещения по дуге эллипса из одного конца большой полуоси в другой.

12.Рассчитайте потенциал электрического поля на оси круглого тонкого кольца с зарядом и радиусом . Заряд считать распределенным равномерно по кольцу.

13.Определите потенциал электрического поля в центре кольца с внешним радиусом 40 см и внутренним – 20 см, если на нем равномерно распределен заряд 0,6 мкК.

14.Коническая поверхность с основанием радиуса равномерно заряжена с поверхностной плотностью . Найдите потенциал электрического поля в вершине конуса.

Практическое занятие №3

Прямая и обратная задачи электростатики

Теория

Решая совместно уравнения Максвелла 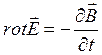и 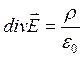в электростатическом случае получают уравнение Пуассона, которое описывает связь потенциала электрического поля с распределением зарядов, то есть связывает полевые характеристики (потенциал) со свойствами среды (объемная плотность заряда)

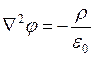. (3.1)

Если в данной точке среды отсутствуют объемные заряды, то получаем частный случай уравнения Пуассона – уравнение Лапласа

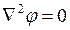. (3.2)

Оператор 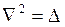– оператор Лапласа, выражение для которого зависит от системы координат.

В декартовой системе координат

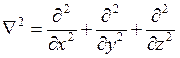; (3.3)
в цилиндрической –

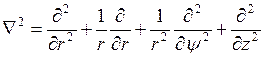; (3.4)
в сферической –

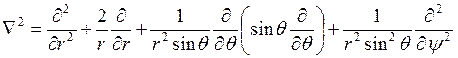.(3.5)

В случае распределения заряда по сфере, шару или цилиндру в силу симметрии запись оператора Лапласа можно сократить:

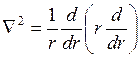, (3.6)

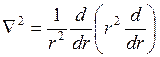. (3.7)

Прямой задачей электростатики называют нахождение потенциала электрического поля по известному распределению заряда

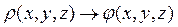, (3.8)

а обратной – нахождение распределения зарядов по известному потенциалу

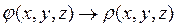. (3.9)

Темы для развернутых ответов

1.  Прямая и обратная задачи электростатики. Примеры.

2.  Уравнение Пуассона и его решение. Привести пример.

Алгоритм решения прямой задачи электростатики
(решения уравнения Пуассона):

1.  По условию задачи найти в заданной точке наблюдения. Записать уравнение Пуассона или Лапласа () в инвариантной форме.

2.  Исходя из симметрии задачи выбирать систему координат так, чтобы потенциал (по возможности) зависел от одной переменной.

3.  Решить дифференциальное уравнение второго порядка. В решение войдут произвольные константы.

4.  Найти значения констант из условий, которым должен соответствовать потенциал – непрерывность и конечность, также используя граничные условия для вектора напряженности электрического поля (если есть граница раздела сред).