Расчет индукции магнитного поля

3.  Дан металлический шар радиуса , окруженный концентрическим слоем диэлектрика с проницаемостью радиусом . Найдите емкость этого шара.

4.  Вычислите емкость сферического конденсатора по данным предыдущей задачи, если вторая металлическая обкладка имеет радиус .

Дополнительный блок задач

5.  Найдите энергию, накопленную в цилиндрическом двухслойном конденсаторе на длине . Рассчитайте его емкость. Внутренний цилиндр имеет радиус , внешний – . Диэлектрик с расположен цилиндрическим слоем радиуса , с – . Все расстояния отсчитываются от оси конденсатора.

6.  Определите взаимную емкость системы, состоящей из металлического шарика радиуса и проводящей плоскости, находящейся на расстоянии от центра шара.

Практическое занятие №6

Расчет индукции магнитного поля

Краткие теоретические сведения

В соответствии с законом Био-Савара-Лапласа индукция магнитного поля, создаваемого элементом тока в точке наблюдения может быть найдена по формуле

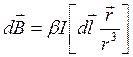. (6.1)

Если ток распределен по некоторому объему, то его магнитное поле рассчитывают как

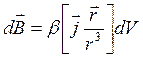, (6.2)

где – плотность тока. Переход от линейных токов к объемным осуществляется с помощью формального перехода

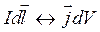. (6.3)

При нахождении индукции магнитного поля, создаваемого несколькими токами, используют принцип суперпозиции

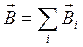, (6.4)

если ток распределен по линии или объему, то от суммирования необходимо перейти к интегрированию (по линии или объему).

Учитывая, что электрический ток есть упорядоченное движение заряженных частиц, запишем индукцию магнитного роля, создаваемого при движении одной частицы

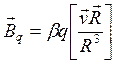. (6.5)

Циркуляцией вектора магнитной индукции называется интеграл вида 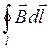. В соответствии с теоремой о циркуляции (или законом полного тока) циркуляция вектора магнитной индукции по произвольной замкнутой кривой равна произведению магнитной постоянной на суммарный ток, пронизывающий площадку, ограниченную данным контуром

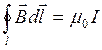. (6.6)

При расчете циркуляции удобно пользоваться проекцией вектора магнитной индукции на касательную к контуру в данной точке . В таком случае математическая запись теоремы о циркуляции примет следующий вид

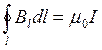.(6.7)

Если магнитное поле, параметры которого мы определяем, создано в некоторой среде, то теорему о циркуляции записывают для вектора напряженности электрического поля

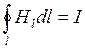, (6.8)

где – сумма макроскопических токов, пронизывающих контур.

В однородном изотропном магнетике индукция магнитного поля связана с напряженностью материальным уравнением

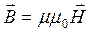. (6.9)

На границе раздела двух сред нормальная составляющая вектора магнитной индукции непрерывна –, тангенциальная составляющая терпит разрыв

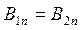, (6.10)

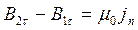, (6.11)

где – плотность поверхностных токов на границе раздела магнетиков.

На элемент тока в магнитном поле действует сила Ампера

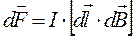, (6.12)

а на движущийся заряд – сила Лоренца

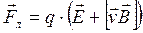. (6.13)

Темы для развернутых ответов

1.  Индукция магнитного поля.

2.  Теорема о циркуляции и ее применение для расчета полей.

3.  Магнитное поле в веществе. Граничные условия.

4.  Силы в магнитном поле.

Литература: [1], глава 6, §35; [3], глава 4, §42-45, 47; глава 5, §60-62.

Основной блок задач

1.  Вычислите индукцию магнитного поля в центре кругового тока радиусом .

2.  Дан круговой ток радиусом . В центре кругового тока восстановлен перпендикуляр к его плоскости. Точка наблюдения находится на расстоянии от плоскости тока на перпендикуляре. Найдите индукцию магнитного поля в точке наблюдения.