Расчет тока в цепи источник методом эквивалентного генератора

рис. 9.23: В,

рис. 9.22: А.

9.5.4.Подставляя значения токов , в уравнение (1), вычисляем значение :

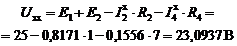
9.5.5. Для расчета заменим в схеме рис. 9.19 источники и их внутренним сопротивлением, равным нулю, и получаем пассивную цепь (рис. 9.24).

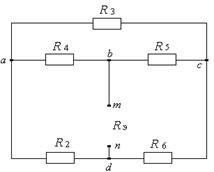
Рисунок 9.24

9.5.6. Для “сворачивания” схемы рис. 9.24 и определения значения необходимо предварительно заменить “треугольник” сопротивлений ,

38

, эквивалентной “звездой”, как это показано в п. п. 9.3.2 и 9.4.1. В результате получим новую цепь (рис. 9.25), которая может быть “свернута” (рис. 9.26).

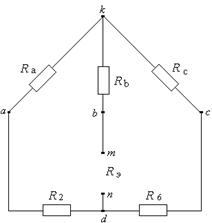
Рисунок 9.25

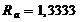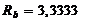Ом,

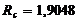Ом,

Ом.

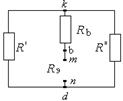
Рисунок 9.26

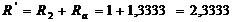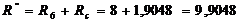Ом,

Ом,

39

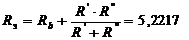Ом.

9.5.7. Таким образом, исходная цепь (см. рис. 9.1)при использовании метода эквивалентного генератора для расчета тока через резистор преобразуется следующим образом (рис. 9.27):

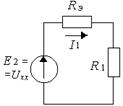
Рисунок 9.27

и, следовательно,

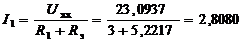А.

Направление тока соответствует направлению напряжения .

9.6 Расчет тока в цепи источника (через резистор ) методом эквивалентного генератора

9.6.1. Заменим исходную схему (см. рис. 9.1) схемой эквивалентного генератора (рис. 9.28), где ток находится по формуле согласно закону Ома:

.

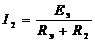40

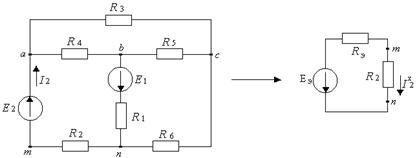
Рисунок 9.28

Так как схемы на рис. 9.28 эквивалентны, напряжение холостого хода с зажимов m n 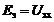будем искать, создав режим холостого хода в исходной схеме и между точками m и n (рис. 9.29).

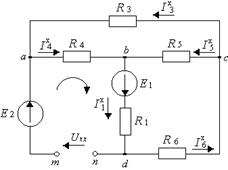
Рисунок 9.29

9.6.2. Выбираем произвольно направления напряжения холостого хода , определяем направления токов в цепи (см. рис 9.29) как токов в простой цепи, напряжения которых определяются полярностью источника ЭДС и составляем уравнения в соответствии со II законом Кирхгофа для контура aвnmd, обходя его по часовой стрелке, как это показано на рис. 9.29:

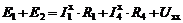. (2)

41

9.6.3. Для расчета значения токов и удалим из схемы (см. рис. 9.29) ветвь am (в ней отсутствует ток) и произведем расчет образовавшейся простой цепи (рис. 9.30) методом “свертывания” (рис. 9.31, 9.32, 9.33):

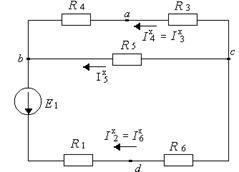
Рисунок 9.30

а) прямой ход

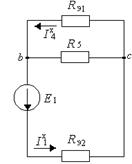
Рисунок 9.31

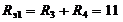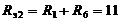Ом,

Ом.

42

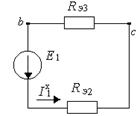
Рисунок 9.32

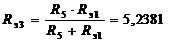Ом.