Расчетные задания по мдтт

Расчетные задания по МДТТ

1.  Напряженное и деформированное состояние цилиндра

Стальной цилиндр, внешний диаметр которого 35.2 см и толщина стенок 5 см, подвергнут действию внутреннего давления 2440 атм. На наружной поверхности цилиндр не нагружен. Определить величины наибольших растягивающих и сжимающих напряжений. Цилиндр предполагать достаточно длинным со свободными торцами, т. е. осевые напряжения в цилиндре – отсутствующими.

Построить графики распределения напряжений в стенке цилиндра.

2.  Напряженное и деформированное состояние цилиндра

Стальной цилиндр, внешний диаметр которого 35.2 см и толщина стенок 5 см, подвергнут действию наружного давления 2000 атм. На внутренней поверхности цилиндр не нагружен. Определить величины наибольших растягивающих и сжимающих напряжений. Цилиндр предполагать достаточно длинным со свободными торцами, т. е. осевые напряжения в цилиндре – отсутствующими. Построить графики распределения напряжений в стенке цилиндра.

3.  Напряженное и деформированное состояние цилиндра

Стальной цилиндр, внешний диаметр которого 35.2 см и толщина стенок 5 см, подвергнут действию внутреннего давления 2000 атм. Наружная поверхность цилиндра жестко заделана в неподвижное основание. Цилиндр предполагать достаточно длинным со свободными торцами, т. е. осевые напряжения в цилиндре – отсутствующими. Предполагать, что в продольном направлении внешняя поверхность цилиндра и неподвижного основания не взаимодействуют. Определить напряженное и деформированное (перемещения) состояние в цилиндре. Построить графики распределения напряжений в стенке цилиндра.

4.  Напряженное и деформированное состояние цилиндра

Стальной цилиндр, внешний диаметр которого 35.2 см и толщина стенок 5 см, подвергается осесимметричному кинематическому нагружению. Точки внутренней поверхности получают перемещение +0.01 мм. Точки наружной поверхности неподвижны. Цилиндр предполагать достаточно длинным со свободными торцами, т. е. осевые напряжения в цилиндре – отсутствующими. Предполагать, что в продольном направлении внешняя поверхность цилиндра и неподвижного основания не взаимодействуют. Определить напряженное и деформированное (перемещения) состояние в цилиндре. Построить графики распределения напряжений в стенке цилиндра.

5.  Напряженное и деформированное состояние толстостенной упругой сферы

Внутри толстостенной сферы действует давление Pa , снаружи – давление Pb . Найти распределение напряжений и перемещений в стенке сферы, построить графики этих зависимостей. Предполагать Pa > Pb . Характеристики материала сферы и величины нагрузок выбрать по своему усмотрению.

6.  Напряженное и деформированное состояние толстостенной упругой сферы

Внутри толстостенной сферы действует давление Pa . Наружная поверхность сферы жестко закреплена в неподвижном фундаменте. Найти распределение напряжений и перемещений в стенке сферы, построить графики этих зависимостей. Характеристики материала сферы и величины нагрузок выбрать по своему усмотрению.

7.  Напряженное состояние составного цилиндра

На вал, диаметр которого d = 10 см, в горячем состоянии надета рубашка, внутренний диаметр которой до нагревания был на 0.001d меньше диаметра вала. Толщина стенок рубашки 10 см. Вал и рубашка – стальные.

Найти напряженное и деформированное состояние рубашки. Построить графики распределений напряжений в рубашке (цилиндре).

8.  Напряженное состояние составного цилиндра

На медный цилиндр с внешним диаметром 40 см и толщиной стенок 10 см плотно надет стальной цилиндр с внутренним диаметром 40 см и внешним 60 см. Точки внутренней поверхности составного цилиндра получают перемещение +0.01 мм. Точки наружной поверхности составного цилиндра неподвижны. Найти распределения напряжений в обоих цилиндрах. Построить графики распределения этих напряжений.

9.  Напряженное состояние составного цилиндра

На медный цилиндр с внешним диаметром 40 см и толщиной стенок 10 см надет стальной цилиндр с внутренним диаметром 40 см и внешним 60 см. Медный цилиндр подвергается действию внутреннего давления 800 атм. Внешняя поверхность наружного цилиндра свободна от нагружения. Найти распределения напряжений в обоих цилиндрах. Построить графики распределения этих напряжений.

10. Напряженное состояние составного цилиндра

На медный диаметр с внешним диаметром 40 см и толщиной стенок 10 см надет стальной цилиндр с внутренним диаметром 40 см и внешним 60 см. Внутренняя поверхность составного цилиндра свободна от нагружения, на внешней действует давление 50 МПа. Найти распределения напряжений в обоих цилиндрах. Построить графики распределения этих напряжений.

11. Напряженное состояние составного цилиндра

Определить напряжения в стенках составного стального цилиндра, если внутренне давление, 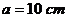, , 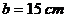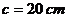и разность радиусов до насаживания 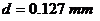. Построить графики распределения этих напряжений в цилиндрах.

12. Напряженное и деформированное состояние упруго-вязкого цилиндра

Длинный толстостенный цилиндр, на внутренней поверхности нагружения нагружается внезапно возникшим давлением, – функция Хевисайда, наружная поверхность цилиндра свободна от нагружения. Материал цилиндра при объемном деформировании демонстрирует чистую упругость, а в отношении деформации формоизменения соответствует реологической модели Кельвина — Фойгта. Найти напряженной и деформированное состояние цилиндра. Построить графики распределения напряжений и перемещений в стенках цилиндра и их зависимости от времени. Динамическими эффектами при деформации цилиндра пренебречь.

13. Напряженное и деформированное состояние упруго-вязкого цилиндра

Длинный толстостенный цилиндр, на внутренней поверхности нагружается кинематически (внезапно задается перемещение), 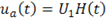, 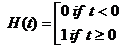– функция Хевисайда, наружная поверхность цилиндра свободна от нагружения. Материал цилиндра при объемном деформировании демонстрирует чистую упругость, а в отношении деформации формоизменения соответствует реологической модели Кельвина — Фойгта. Найти напряженной и деформированное состояние цилиндра. Построить графики распределения напряжений и перемещений в стенках цилиндра и их зависимости от времени. Динамическими эффектами при деформации цилиндра пренебречь.

14. Напряженное и деформированное состояние упруго-вязкого цилиндра

внезапно возникшим давлением, — функция Хевисайда, наружная поверхность цилиндра свободна от нагружения. Материал цилиндра при объемном деформировании демонстрирует чистую упругость, а в отношении деформации формоизменения соответствует реологической модели Максвелла. Найти напряженной и деформированное состояние цилиндра. Построить графики распределения напряжений и перемещений в стенках цилиндра и их зависимости от времени. Динамическими эффектами при деформации цилиндра пренебречь.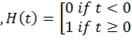

15. Напряженное и деформированное состояние упруго-вязкого цилиндра

Длинный толстостенный цилиндр, на внутренней поверхности нагружается кинематически (внезапно задается перемещение), 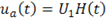, 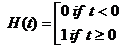– функция Хевисайда, наружная поверхность цилиндра свободна от нагружения. Материал цилиндра при объемном деформировании демонстрирует чистую упругость, а в отношении деформации формоизменения соответствует реологической модели Максвелла. Найти напряженной и деформированное состояние цилиндра. Построить графики распределения напряжений и перемещений в стенках цилиндра и их зависимости от времени. Динамическими эффектами при деформации цилиндра пренебречь.

16. Напряженное состояние составного цилиндра

Рассмотреть напряженное и деформированное состояние составного длинного цилиндра, внутренняя часть которого выполнена из чисто вязкого материала, а наружная – из упругого. Все материальные параметры и параметры нагружения для демонстрационных расчетов выбрать по своему усмотрению. Предположить, что цилиндр подвергается нагружению внезапно возникшим внутренним давлением