Распространение луча света

Таким образом, получили, что 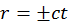. Так как речь идет о распространении света, такой конус называют световым конусом или гиперконусом (рис. 13). Образующая конуса – есть траектория луча света или его мировая линия в четырехмерном пространстве.

Мы можем нарисовать сечение этого конуса плоскостью.

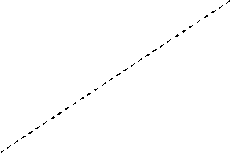
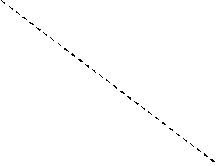
Световой конус делит все четырехмерное пространство так, что все реальные события, которые могут произойти в природе, располагаются внутри этого конуса.

Убедимся в этом. Рассмотрим несколько частных случаев.

1.  Распространение луча света.

Соответствует точкам, расположенным по поверхности светового конуса.

2.  Рассмотрим движение частицы в четырехмерном пространстве. Если частица движется равномерно и прямолинейно и при проходит через начало координат, то при движении вдоль оси Х в трехмерном пространстве ее мировая линия в четырехмерном пространстве есть следующая величина:

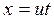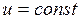; . (1.6.9)

Домножим и поделим на :

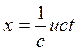. (1.6.10)

Введем обозначение 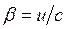и получим в итоге:

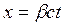— уравнение прямой.

Следует отметить, что коэффициент всегда меньше единицы (за счет того, что ). Таким образом, угол наклона прямолинейной траектории равномерного движения в сечении 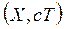четырехмерного пространства всегда лежит в пределах (рис. 1.10).

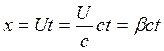(1.6.11)

Это какая-то мировая линия, причем 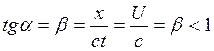. Т. е. всегда .

3.  Частица покоится в начале координат, т. е. x=y=z=0

Мировая линия – это прямая, совпадающая с осью cT.

3.  Рассмотрим произвольно движущуюся частицу.

r(t) – произвольная функция

Тангенс угла наклона в любой точке будет меньше единицы.

§ 1.7. Четырехмерные векторы

Четырехмерный вектор – совокупность четырех величин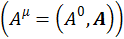, которые при переходе от одной инерциальной системе координат к другой преобразуется по закону:

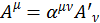(1.7.1)

Запишем преобразования Лоренца для произвольного четырехмерного вектора, когда штрихованная система движется относительно нештрихованной системы вдоль оси ОХ. Для этого произведем следующую замену в уже известных нам формулах 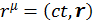и :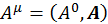

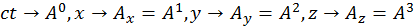(1.7.2)

Подставив новые переменные в преобразования Лоренца, получим:

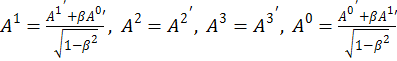(1.7.3)

Это и есть искомые преобразования Лоренца.

Все четырехмерные векторы обладают свойством, что их скалярные произведения

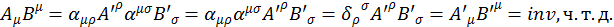(1.7.4)

Все четырехмерные векторы делятся на:

1)  Пространственноподобные

2)  Временеподобные

3)  Светоподобные

В этом можно убедиться из следующих соображений.

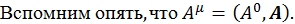
Среди всех можно найти такое, которое удовлетворяет следующему условию:

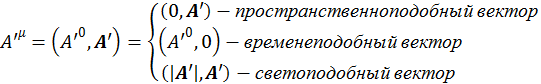(1.7.5)

Все эти векторы различаются также по величине квадрата в скалярном произведении.

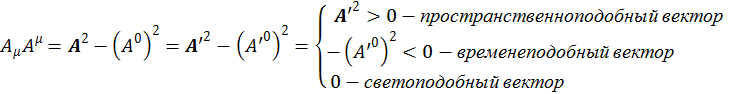
В качестве штрихованной системы мы здесь выбирали систему покоя частицы.

Рассмотрим примеры четырехмерных векторов.

1.  Четырехмерный радиус-вектор. Он определяется как

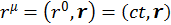(1.7.6)

и является временеподобным, т. к

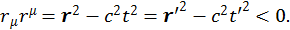(1.7.7)