Растяжение — сжатие
Действует поперечная сила ![]() – это срез (сдвиг);
– это срез (сдвиг);
Действует крутящий момент ![]() – это кручение;
– это кручение;
Действует изгибающий момент ![]() – это “чистый изгиб”.
– это “чистый изгиб”.
3 Растяжение (сжатие)
Растяжением (сжатием) называется такой вид деформации, при котором в поперечном сечении бруса возникает только продольная сила ![]() , а все остальные внутренние усилия равны нулю.
, а все остальные внутренние усилия равны нулю.
При растяжении (сжатии) продольная сила, направленная по нормали от сечения – положительна, если по нормали к сечению – отрицательна.
Продольная сила в сечении определяется методом сквозного разреза. Она численно равна алгебраической сумме внешних сил, действующих вдоль оси стержня по одну сторону от сечения, и противоположно направлена.
Для выяснения закона распределения продольных сил по длине стержня строится эпюра ![]() (рис. 2).
(рис. 2).
Определение значения продольной силы на каждом силовом участке:
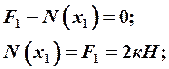
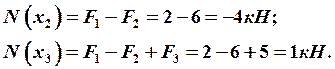
Эпюрой называется график, показывающий закон изменения какого-либо силового фактора по длине элемента конструкции.
Любая ордината эпюры показывает величину силового фактора в сечении, расположенном против данной ординаты.
Рис. 2 Эпюра продольных сил
Скачки на эпюре равны величинам внешних продольных сил, приложенных в соответствующих сечениях.
Решаются три вида задач расчета на прочность:
1. Исходя из критерия прочности при растяжении (сжатии) определяется площадь поперечного сечения стержня:
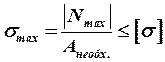 ;
; 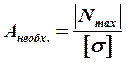 . (1)
. (1)
2. Определяется несущая способность (грузоподъемность) стержня:
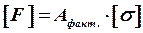 . (2)
. (2)
3. Проверяются фактические напряжения:
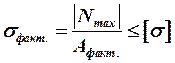 . (3)
. (3)
Расчет на жесткость проводится по следующей формуле:
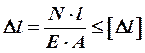 . (4)
. (4)
Абсолютная деформация ![]() пропорциональна продольной силе
пропорциональна продольной силе ![]() , действующей на силовом участке длиной
, действующей на силовом участке длиной ![]() и обратно пропорциональна жесткости при растяжении (сжатии) –
и обратно пропорциональна жесткости при растяжении (сжатии) –![]() .
.
4 Кручение
Кручением называется такой вид напряженного и деформируемого состояния, при котором в поперечном сечении круглого стержня возникает только один внутренний силовой фактор, – крутящий момент ![]() , действующий в плоскости сечения.
, действующий в плоскости сечения.
Крутящий момент, действующий в каком-либо сечении на левую часть бруса, равен и противоположно направлен крутящему моменту, действующему в том же сечении на его правую часть. Следовательно, кручение является примером чистого сдвига, при котором в поперечном сечении возникают только касательные напряжения.
На основании метода сквозного разреза, крутящий момент в произвольном поперечном сечении стержня численно равен алгебраической сумме внешних скручивающих моментов, действующих по одну сторону от сечения, и направлен в противоположную сторону по отношению к их равнодействующему моменту.
Крутящий момент является положительным, если внешний скручивающий момент поворачивает круглый вал по часовой стрелке, если смотреть со стороны разреза.
Правило остаётся неизменным для любой рассматриваемой части вала – левой или правой. Пример построения эпюр показан на рис. 6.
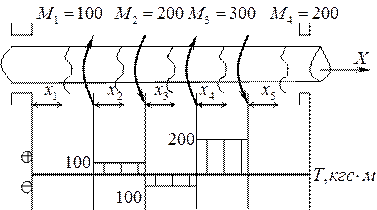
Рис. 3 Эпюра крутящих моментов
Определяем значения крутящих моментов на каждом силовом участке:
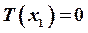 ;
; 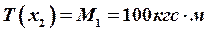 ;
;
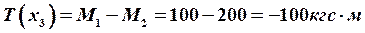 ;
;
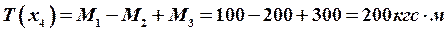 ;
;
![]() .
.
При рассмотрении эпюр учитываются следующие факторы: крутящие моменты в опорных сечениях равны нулю, если опоры подшипники; скачки на эпюре ![]() равны величине скручивающих моментов, приложенных в данном сечении; расчет на прочность производится по наибольшей абсолютной величине крутящего момента. В данном примере это
равны величине скручивающих моментов, приложенных в данном сечении; расчет на прочность производится по наибольшей абсолютной величине крутящего момента. В данном примере это 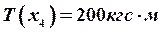 .
.
Критерий прочности при кручении имеет вид
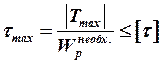 , (5)
, (5)
где 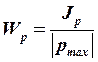 – полярный момент сопротивления, см3;
– полярный момент сопротивления, см3;
![]() – максимальный крутящий момент;
– максимальный крутящий момент;
![]() – допускаемые напряжения при кручении.
– допускаемые напряжения при кручении.
Подбор поперечного сечения осуществляется по формуле
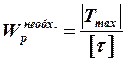 . (6)
. (6)
Для расчета сплошных и полых валов по формулам (5) и (6) необходимо определять полярные момент инерции ![]() и момент сопротивления
и момент сопротивления ![]() , выразив данные характеристики через диаметр.
, выразив данные характеристики через диаметр.
Для сплошного вала
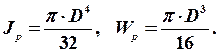 (7)
(7)
Для полого вала
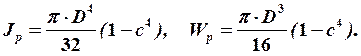 (8)
(8)
где 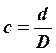 .
.
Значение ![]() позволяет подобрать диаметр вала по формулам:
позволяет подобрать диаметр вала по формулам:
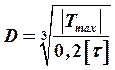 ,
, 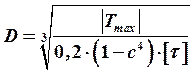 . (9)
. (9)
Расчет на жесткость при кручении проводится по следующей формуле:
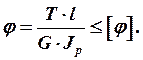 (10)
(10)


