Равномерный путевой расход

Рис. 6.8

Очевидно, что ; ;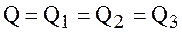

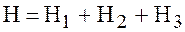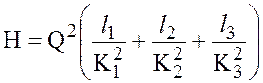. (6.6)

Суммарную характеристику можно получить по выражению (6.6) или построением характеристик отдельных ее участков 1,2 и 3 с последующим графическим их сложением (рис.6.9).

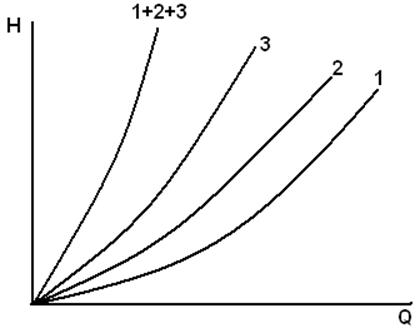
Рис. 6.9

7. гидравлическая сеть состоит из нескольких трубопроводов различного диаметра и длины, соединенных параллельно (рис. 6.10).

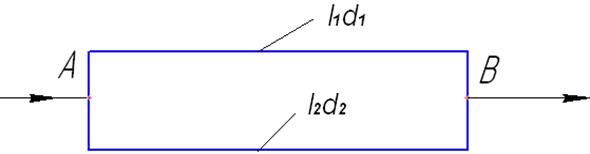
Рис. 6.10

Очевидно, что 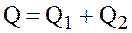. В точках А и В напор одинаков для трубопровода с расходом Q1 и Q2. следовательно, падение напора в каждой ветке одинаково, т. е. Н=Н1=Н2 или

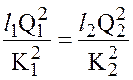. (6.7)

Суммарную характеристику получают построением характеристик отдельных ее участков с последующим графическим их сложением (рис.6.11).

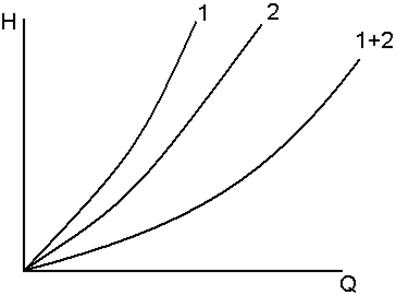
Рис. 6.11

6.4. Равномерный путевой расход

Во многих случаях приходится рассчитывать устройства, в которых жидкость расходуется равномерно по длине трубопровода. Это дождевальные и моечные устройства. Кроме того, например, уличный трубопровод системы водоснабжения несмотря на неравномерность расхода по его длине, рассчитывается как трубопровод с равномерным расходом.

Равномерный путевой расход характеризуется интенсивностью .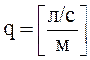

В общем случае, кроме путевого расхода, данный участок l пропускает некоторый транзитный расход Qт (рис. 6.12).

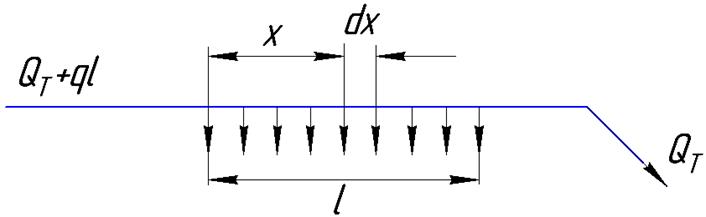
Рис.6.12

Общий расход в начальном сечении участка Q = QT+ql.

Определим линейные потери напора на участке l. Для этого рассмотрим сначала элемент участка dx, расположенный на расстоянии х от начала.

Через рассматриваемый элемент dx проходит весь транзитный расход Qт, а также та часть путевого расхода, которая следует на участке l-х:

.

Для определения линейных потерь на участке l воспользуемся формулой 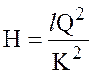, представив ее в виде

.

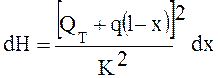Тогда потери напора на участке l

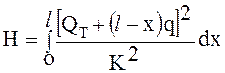. (6.8)

Выражение (6.8) легко интегрируется для квадратичной зоны графика Никурадзе. В этом случае K = сonst. Имея в виду, что Qn=ql, получим:

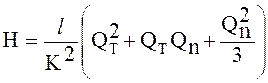. (6.9)

В том случае, если транзитный расход Qт отсутствует, получаем:

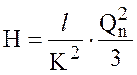. (6.10)

Таким образом, при отсутствии транзитного расхода равномерный расход эквивалентен расходу, сосредоточенному на конце участка:

.

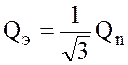6.5. Гидравлический удар в трубопроводах. Гидравлический таран

Гидравлическим ударом называется резкое изменение давле*ния в напорном трубопроводе вследствие внезапного изменения скорости движения жидкости во времени. Рассмотрим сущность явления.

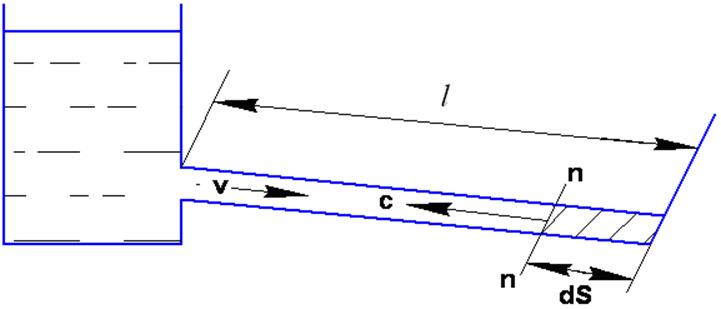
Рис. 6.13

Предположим, что в трубопроводе (рис.6.13) длиной l движется жидкость под давлением ро со скоростью V. Закроем мгновенно заслонку. Ввиду сжимаемости жидкости, хотя незначительной, мгновенно во всем трубопроводе она остановиться не может. Останавливается сначала какой-то слой у заслонки, а вся остальная жидкость слева продолжает двигаться с прежней скоростью. Но постепенно граница подвижной и неподвижной жидкости n-n продолжает перемещаться от заслонки к резервуару со скоростью, которая называется скоростью распространения ударной волны С.

В тот момент, когда вся жидкость в трубопроводе остановится, давление у заслонки станет максимальным. При этом часть жидкости из резервуара войдет в трубу. Ввиду повышенного давления у заслонки жидкость придет в движение от заслонки к резервуару и давление у заслонки установится равным нормальному ро. Жидкость, двигаясь в сторону резервуара, по инерции старается оторваться от заслонки, у которой давление становится меньше нормального. Теперь фронт пониженного давления перемещается к резервуару. Затем фронт нормального давления перемещается в сторону заслонки, и когда оно у заслонки становится нормальным, заканчивается первый цикл гидравлического удара (рис.6.14), состоящий из фаз повышенного и пониженного давления.

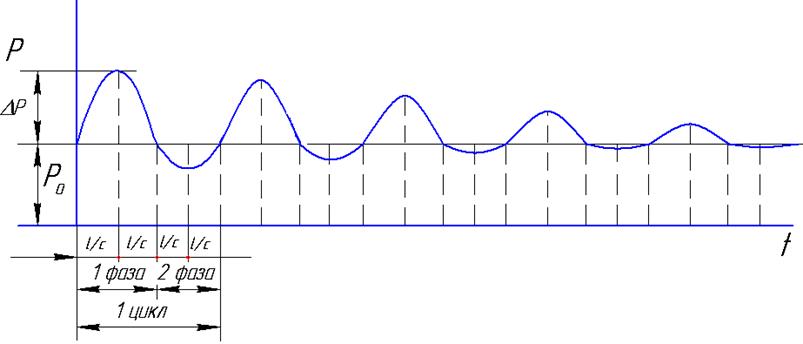
Рис. 6.14

Так как заслонка закрыта, то начиная со второй фазы, процесс начнет повторяться. Часть энергии жидкости при этом переходит в тепло, поэтому амплитуда колебаний давления с течением времени затухает и процесс прекращается.

Наибольшую опасность представляет прямой гидравлический удар, когда время закрытия заслонки 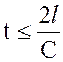. Давление при этом будет максимальным и больше нормального на величину Δр.

Найдем расчетные зависимости для определения величины Δр. Для этого применим теорему об изменении количества движения, смысл которой сводится к тому, что изменение количества движения равно импульсу силы.

Рассмотрим объем жидкости от заслонки до сечения n-n длиной dS и площадью поперечного сечения ω. Остановившаяся масса жидкости в этом объеме потеряла некоторое количество движения за время dt в течение, которого слой передвинулся от заслонки влево на расстояние dS:

.

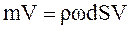Импульс силы за тот же промежуток времени

.

Приравняем импульс силы к количеству движения, получим

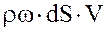=, откуда

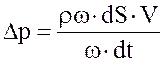или

, (6.11)

где 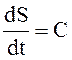— скорость распространения ударной волны.

Формула (6.11) впервые была получена Н. Е. Жуковским. Он показал, что скорость распространения ударной волны С для абсолютно жестких стенок равна скорости распространения звука в воде:

,

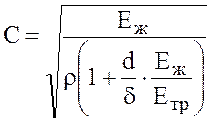где — соответственно диаметр и толщина стенок трубы; Еж, Етр – соответственно модули упругости жидкости и материала трубы; — плотность жидкости.

Приближенно для водопроводных труб Δρ=(10…14)V ат при V м/с.

Для предупреждения прямого гидравлического удара запорную арматуру выполняют медленнозакрывающейся.