Релятивистская механика

Подтверждением этому являются электромагнитные волны. Это физическое явление имеет право на существование благодаря наличию этих инвариантов.

Дадим общее доказательство инвариантности тензоров.

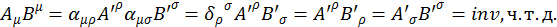(1.12.10)

Глава II

РЕЛЯТИВИСТСКАЯ МЕХАНИКА

§ 2.1. Четырехмерные векторы импульса и силы

Основные механические переменные в механике Ньютона — импульс, сила, энергия, мощность, момент импульса — определены в предположении абсолютного времени (t=t′=t′′=…). В релятивистской механике это предположение не верно, здесь инвариантом является только одно время – собственное время τ. Поэтому все динамические переменные в релятивистской механике нуждаются в переопределении и все они должны являться в четырехмерными векторами или тензорами второго ранга.

В механике Ньютона импульс определяется как 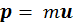, где u – ньютоновская скорость. Необходимо осуществить переход от трехмерного к четырехмерному вектору импульса:

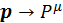. (2.1.1)

Четырехмерный вектор импульса должен иметь вид

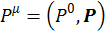(2.1.2)

Обозначим

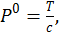(2.1.3)

где Т имеет размерность энергии. Согласно Ньютону, импульс должен быть пропорционален скорости, значит для четырехмерного вектора импульса:

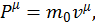(2.1.4)

где должна быть инвариантом, чтобы справа и слева стояли четырехмерные вектора. Мы определим позже, но сразу оговорим, что это величина будет иметь размерность массы.

Подставив (2.1.3) в формулу (2.1.2) и используя определение четырехмерной скорости, можно записать:

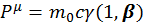(2.1.5)

Сравнивая формулы (2.1.2) и (2.1.5), находим:

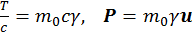(2.1.6)

Причем, т. к. p=mu, то можно сделать вывод, что

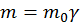(2.1.7)

Из этой формулы видно, что при β→0 m=m0,т. е. это собственная масса частицы. Эта величина является характеристикой самой частицы. При β→1 m→∞ и эта «масса» может принимать очень большие значения. Ее можно назвать относительной массой.

Из формулы (2.1.6) можно выразить

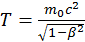(2.1.8)

Видно, что при β→0

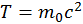(2.1.9)

Эта формула для энергии покоя, полученная Эйнштейном. Она означает, что покоящаяся частица обладает энергией, которая, например, может частично выделится в процессе распада.

Рассмотрим теперь нерелятивистское приближение (β2<<1). Разложим по малым β2:

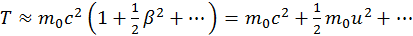(2.1.10)

Видно, что второе слагаемое есть не что иное, как кинетическая энергия движущейся частицы. Таким образом, физический смысл состоит в том, что это кинетическая энергия частицы вместе с энергией покоя:

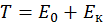. (2.1.11)

Оказывается, все четыре компоненты не являются независимыми. Это связано с тем, что

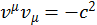(2.1.12)

При домножении обеих частей уравнения на , получим

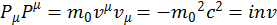. (2.1.13)

Или можно переписать это уравнение в другом виде:

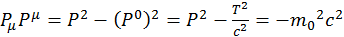(2.1.14)

Последнее соотношение между P2, m02 и может быть записано как:

или 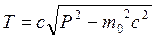. (2.1.15)

Учитывая формулу (2.1.6) получаем, что из инвариантности 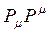следует энергия в виде:

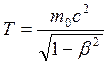. (2.1.16)

Определим теперь четырехмерный вектор силы. Из второго закона Ньютона сила есть

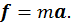(2.1.17)

В релятивистской механике ему соответствует четырехмерный вектор:

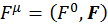(2.1.18)

В классической механике сила пропорциональна ускорению, значит для формула (2.1.17) выглядит как:

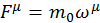, (2.1.19)

где есть уже определенная выше масса покоя частицы.

Выясним теперь физический смысл нулевой компоненты четырехмерного вектора силы. Из определения видно, что:

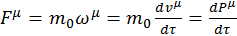. (2.1.20)

Обозначим

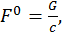(2.1.21)

Где G имеет размерность мощности. Тогда

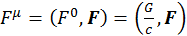(2.1.22)

Попробуем найти аналог F в механике Ньютона:

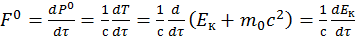(2.1.23)

Введя промежуточную производную по , получаем:

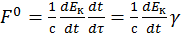(2.1.24)

Перейдя теперь к нерелятивистскому приближению 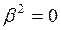, имеем: