Решение двухточечной краевой задачи на языке с++

1.  Задание исследования

Провести исследование решения двухточечной краевой задачи методом прогонки на языке С++.

2. Подробное описание задачи и методы её решения

Физические процессы часто описываются обыкновенными линейными дифференциальными уравнениями второго порядка. В некоторых случаях представляет интерес описание процесса на некотором интервале изменения аргумента при условии, что на обеих границах этого интервала заданы значения линейных комбинаций состояний процесса и его первых производных. Такая задача называется линейной двухточечной краевой задачей и может быть решена с помощью так называемого метода прогонки. Метод прогонки часто еще называют алгоритмом Томаса.

Сначала требуется найти функцию y(x), на отрезке [a, b], которая удовлетворяет следующему дифференциальному уравнению и краевым условиям:

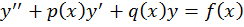
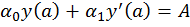
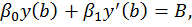
где p(x), q(x), f(x) — известные непрерывные на отрезке [a, b] функции, 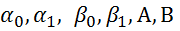— заданные постоянные, причем .

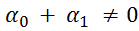Предполагается, что отрезок [a, b], на котором будет находиться решение этого уравнения, разбит на n равных частей системой точек (сеткой).

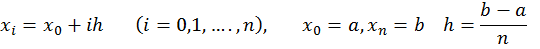
Пусть pi, qi, fi, yi — значения соответствующих функций в узлах сетки. Тогда вычисления производятся в два приема (прямой ход и обратных ход ) следующем порядке:

·  Прямой ход:

Вычислить набор значений mi и ki по формулам:

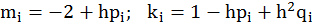, (i=0,1,…..,n-2)

Затем находим набор значений ci и di:

,

;

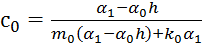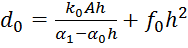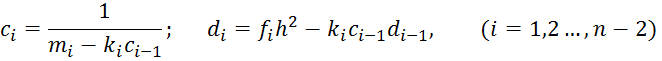
·  Обратный ход:

Находим все значения функции yi:

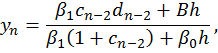
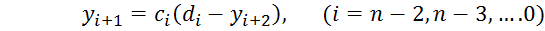
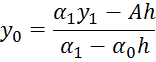
Таким образом, все вычисления как бы прогоняют два раза. Вычисления прямого хода заготавливают вспомогательные числа ci и di в порядке возрастания индекса i. При этом для вычисления с0, d0 используется краевое условие на левом конце отрезка интегрирования. Затем на первом шаге обратного хода происходит согласование полученных чисел сn-2, dn-2 с краевым условием на первом конце отрезка интегрирования, после чего последовательно получаются значения искомой функции yi в порядке убывания индекса i.

Примените метод прогонки для приближенного решения следующей краевой задачи:

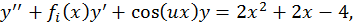
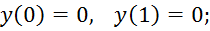
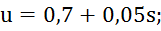
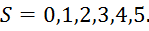
3. Описание работы программы и результаты исследований

Программа написана на языке С и является консольным приложением. Данная программа позволяет получить решение вышеуказанного уравнения на интервале от ab[0;1] в точках Xn с шагом h=(b-a)/n, где n – число точек на интервале, при параметрах fi и S. Значения fi приведены в таблице. S же, изменяется от нуля до пяти, с шагом в единицу.

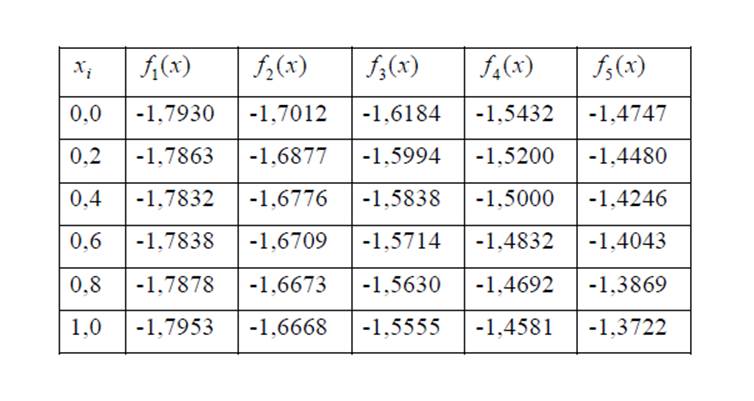
При запуске программы происходит последовательный расчет значений искомой функции в зависимости от S от первого значения f. Затем выполняется замена значений f в точках на следующее. Рассчитываются значения для всех S (от 0 до 5). Все результаты промежуточных вычислений выводятся на экран.

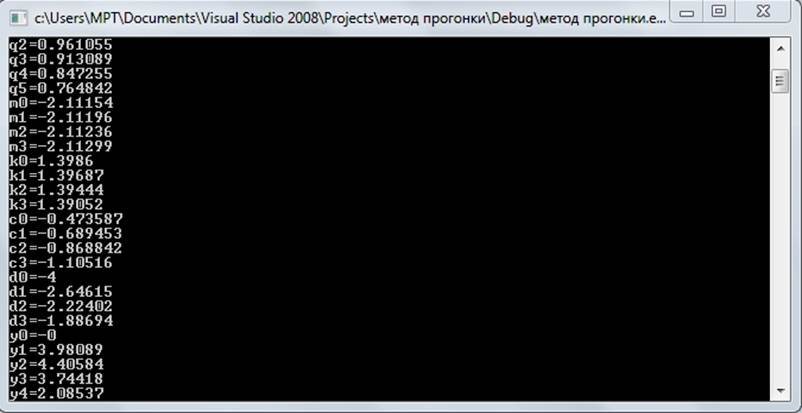
Окончательным результатом программы являются значения yi при разных значениях S и f. В ходе работы программы все полученные значения функции в шести точках (краевые значения равны нулю), номер fi, значение S записываются в файл “пакет. xls”, находящийся в корневой папке программы.

3.1 Анализ зависимостей результатов программы

Для f1:

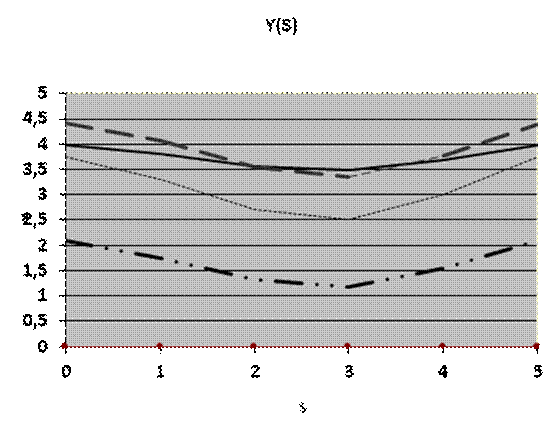
Рис. 1.1 — График влияния величины S на функцию Y.

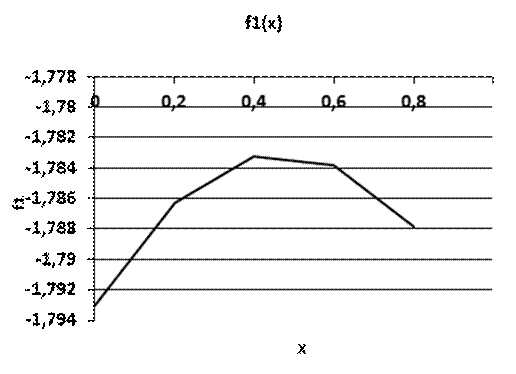
Рис. 1.2 График функции f1(X)

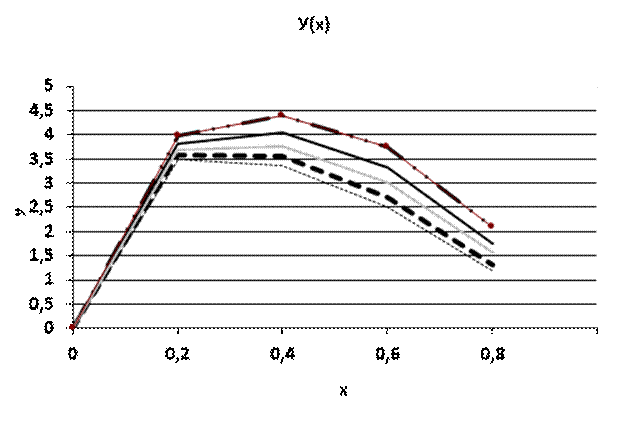
Рис.1.3 График функции Y(X) при разных значениях S.

Для f2:

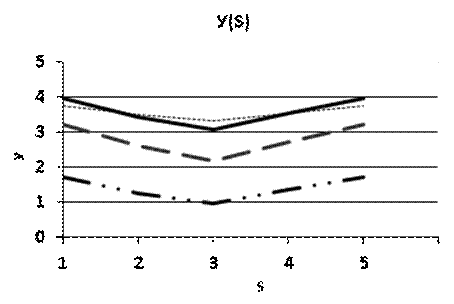
Рис.2.1 График влияния величины S на функцию Y.

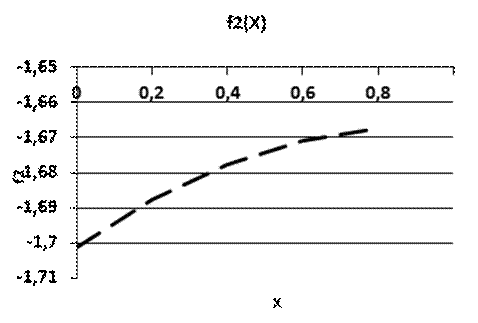
Рис.2.2 График функции f2(X)

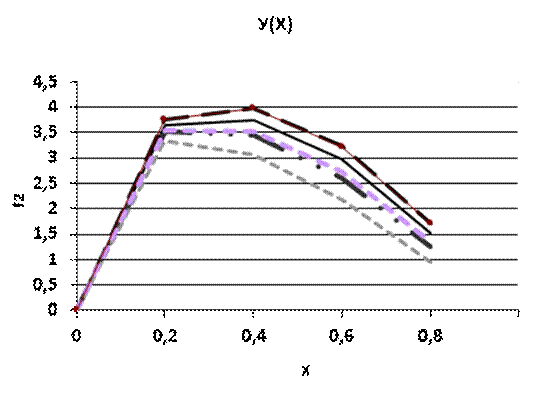Рис.2.3 График функции Y(X)

Для f3:

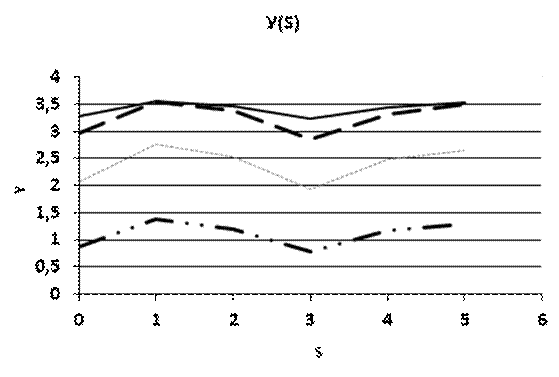
Рис. 3.1 График влияние величины S на функцию Y.

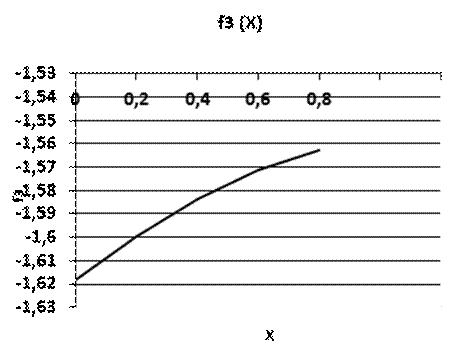
Рис. 3.2 График функции f3(X)

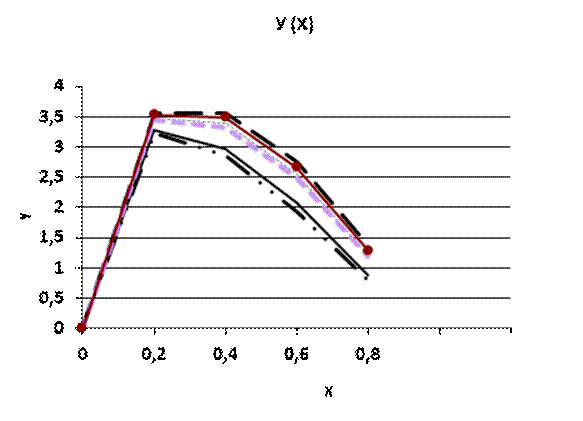
Рис. 3.3 График функции Y(X)

Для f4:

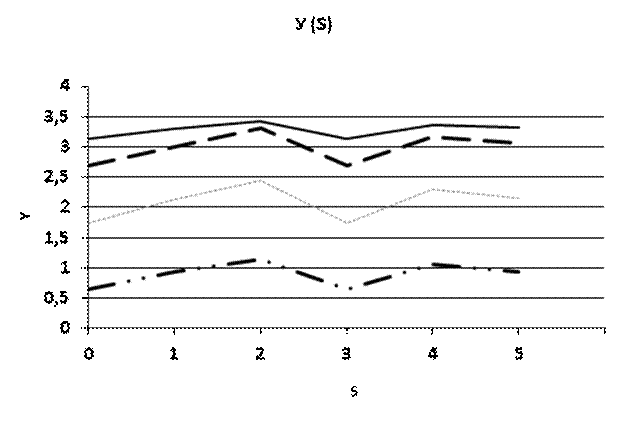
Рис. 4.1 График влияние величины S на функцию Y.

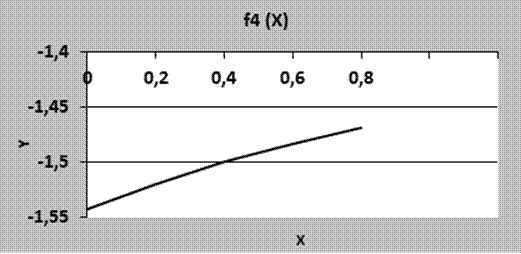
Рис.4.2 График функции f4(X)

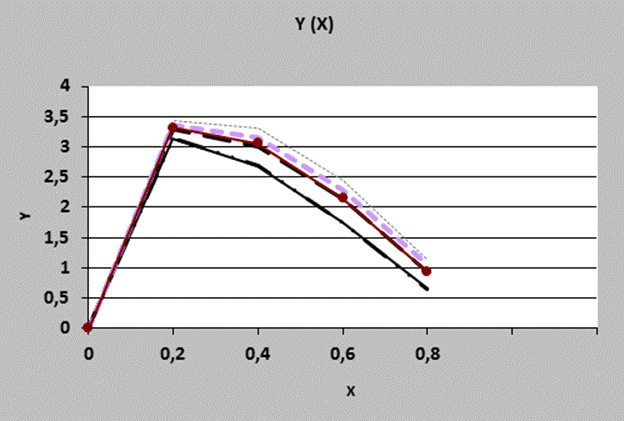
Рис. 4.3 График функции Y(X)

Для f5:

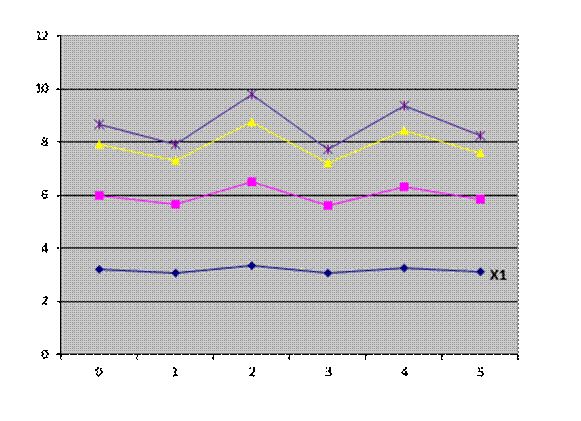
Рис. 5.1 График влияние величины S на функцию Y

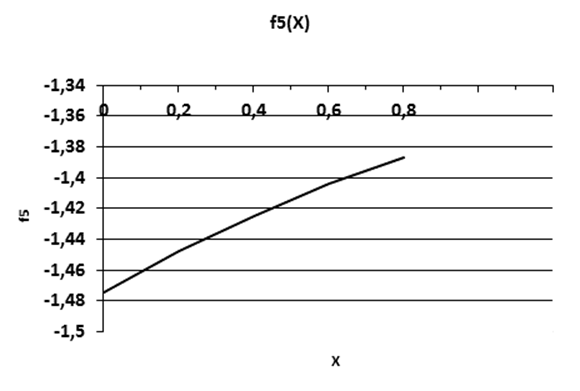
Рис. 5.2 График функции f5(X)

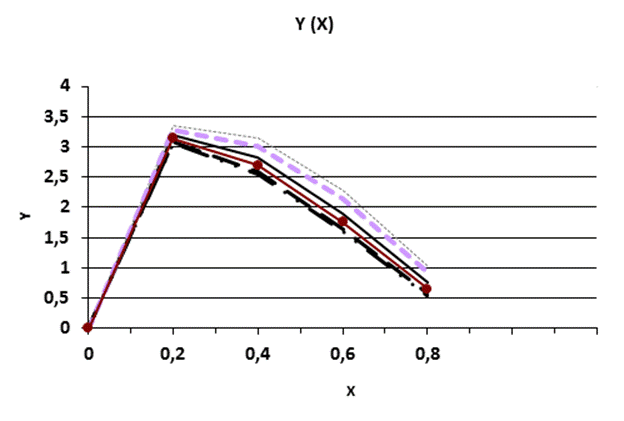
Рис. 5.3 График функции Y(X)

4. Выводы

В данной работе был исследован метод прогонки в применении к двухточечной краевой задаче. Для этого была написана программа, с помощью которой можно получить решения уравнения данным методом.

В ходе выполнения исследования была установлена зависимость величины корней предложенного дифференциального уравнения от номера функции fi. Зависимость обратно пропорциональная. Помимо этого, от номера функции зависит еще и число точек экстремума для графиков корня Y от S, также, с ростом номера f, меняетcя значение ( даже по знаку) производной Y в точке Х=0,4. Параметр S заставляет функцию колебаться в неких пределах. Это следствие связи S с аргументом косинуса. Также, по — видимому, наблюдается зависимость меж формой графика функции f и величиной второго корня уравнения.

Влияние S, а также связанное с S влияние f. См. график влияния величины S на функцию Y.

Из графиков следует, что изначально, для первой функции, достигается экстремум только при одном значении S, а именно S = 3. В дальнейшем, со сменой функции fi число точек экстремума тоже растет, будучи равным i. Видно, что, для каждой из функций наблюдается изменение значений в пределах некого интервала, зависящее от S. . Стоит заметить, что упомянутый интервал имеет некие четкие границы в виду того, что S влияет на u – один из множителей аргумент косинуса. Обобщая, сажем, что из приведенных графиков можно сделать вывод, что S влияет на значение функции в неких пределах. От номера же функции f зависит еще и число точек экстремума, то есть, точек равенства нулю первой производной функции. Иначе говоря, от номера функции зависит увеличится или уменьшится значение Y с изменением S.

Заметна связь меж формой f и S на графике влияния величины S на функцию Y.

График для второго корня уравнения, в зависимости от формы графика f, в той или иной степени уходит в диапазон значений графика для первого корня. Затем, при изменении номера функции( с повышением номера график «выпрямляется») наблюдается постепенное изменение графика значений второго корня, в зависимости от S, в сторону подобия графикам остальных корней.

Влияние f на форму графика. См. графики функции Y(X).

Также, можно сделать вывод, что для каждой последующей функции fi значение функции Y меньше, чем для каждой предыдущей(сравниваем графики для разных f). Учитывая, что для каждой последующей fi значение в точке Xn больше, чем для каждой предыдущей, наблюдаем обратнопропорциональную зависимость величины функции Y от величины функции f. Наблюдается кажущееся нарушение описанной зависимости для f5. Это происходит т. к. первое значение(X=0) больше, чем значение f4 для Х=5, что не выполняется для всех прочих f. Наблюдается, помимо всего прочего, явление заметного изменения величины производной функции Y для любого S в точке X=0,4. С увеличением номера функции f, все больше графиков в этой точке меняют возрастание на убывание.

5. Приложение

5.1 Описание применения

5.1.1  Назначение программы

Программа метод прогонки предназначена для исследования метода прогонки при решении двухточечной краевой задачи вида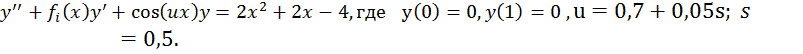

Программа применяется для нахождения решения двухточечной краевой задачи методам прогонки. Результаты вычисления записываются в файл пакет. xls, предназначенный для работы в Microsoft Excel 2007.

5.1.2  Условия применения

Программа может быть применена на большинстве персональных компьютеров, поддерживающих операционную систему Windows с возможностью запуска консольных приложений.

5.1.3  Описание задачи

Вычисления значения приближенного решения краевой задачи методом прогонки.

5.2 Программа и методика испытаний

5.2.1  Объект испытаний

Объектом испытаний является программа метод прогонки . Программа метод прогонки предназначена для исследования метода прогонки при решении двухточечной краевой задачи для функций вида 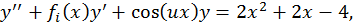с заданными начальными условиями.

5.2.2  Цель испытаний

Цель испытаний — удостовериться в том, что программа выполняет все возложенные на неё функции и задачи. А также не содержит ошибок в исполнении.

5.2.3 Средства и порядок испытаний

Для испытания данной программы были использованы следующие технические и программные средства:

— Ноутбук PACKARD BELL Easy Note TK85 c процессором Intel(R) Core(TM) i3 CPU M370 2.40 GHz, 2.40 GHz и 3 гигабайтами оперативной памяти, оснащенный ОС MS Windows 7 Домашняя базовая.

— Программа Microsoft Visual Studio 2008.

Испытания следует проводить на той же вычислительной установке, на которой была отлажена и проверена программа метод прогонки . Для испытаний нужно иметь:

–  Программа метод прогонки;

Необходимо провести запуск программы метод прогонки и получить файл с результатами расчета методом прогонки.

5.2.4  Способы тестирования программы

Тестирование работы написанной программы проводилось путем решения дифференциального уравнения в заданной точке при помощи операционного исчисления (преобразования Лапласа). Ошибка не превысила пяти процентов даже с учетом округлений в процессе решения. Кроме того, изначальные данные для решения поставленной задачи говорят, что в крайних точках интервала значение функции Y равняется нулю, что наблюдалось в процессе работы программы. В результате был сделан вывод, что программа работает верно.

Значение, полученное для функции с помощью преобразований Лапласа при равенстве S=0, X=0,2, f(X)=-1,7863, имеет величину 3,81. C учетом округлений в процессе решения «в ручную», и равенства значения, выдаваемого программой, 3,987, будем считать работу программы верной.

5.3  Руководство пользователя

5.3.1  Назначение программы

Программа метод прогонки предназначена для исследования метода прогонки при решении двухточечной краевой задачи для функций вида 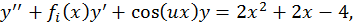где известны параметры u, x и s.

5.3.2  Условия и характеристики программы

Программа может быть применена на большинстве персональных компьютеров, поддерживающих операционную систему Windows с возможностью запуска консольных приложений.

5.3.3  Выполнение программы

Для вызова программы необходимо перейти в каталог программы и запустить файл метод прогонки. exe.

5.3.4 Входные и выходные данные

Входными данными для этой программы являются номер fi и s (s=0,5). После ввода входных данных не обязательно нажать клавишу Enter.

Выходные данные: значения функции Y(X), рассчитанные методом прогонки для всех s и f. Результат выводится на экран и сохраняется в файл с расширением xls.

5.3.5 Сборка программы

Средой разработки программы является Microsoft Visual Studio 2008. Программа написана на языке С++.

5.3.6 Текст программы

#include <stdio. h>

#include <math. h>

#include "stdafx. h"

#include <windows. h>

#include <iostream>

#include <conio. h>

#include <time. h>

#include <ctime>

#include <stdlib. h>

#include <string. h>

#include <locale. h>

#include <stdio. h>

#include <stdlib. h>

#include <conio. h>

#include <math. h>

using namespace std;

int _tmain(int argc, _TCHAR* argv[])

{

setlocale( LC_ALL, "Russian" ); //и вот эта команда

float y0=0;// значения функции У на концах интервала

float y1=1;

float A=0;

float B=0;

float a=0;// концы

float b=1;

float a0=1;// для ЛК. Берем из логики рисунка + задания.

float a1=0;

float b0=1;

float b1=0;

int Nom;

int n=5;

int u=1;

int s;

float h= (b-a)/n;

float im=0;

//функция перед 1й производной/ Значения записываются по fi, после чего изменяется Xi. Строчка

float p[6];

cout<<"VVEDI NOMER FUNC 1-5";

//cin>> Nom;

FILE * f = fopen("пакет. xls","w+");

fseek(f, 0, SEEK_END);

int z = ftell(f);

fseek(f, 0, SEEK_SET);

fprintf (f, "%s" ,"n");

for(Nom=1;Nom<6;Nom++)

{switch (Nom)

{

case 1:

{

p[0]= -1.7930;

p[1]= -1.7863;

p[2]= -1.7800;

p[3]= -1.7700;

p[4]= -1.7600;

p[5]= -1.7500;

break;

}

case 2:

{

p[0]= -1.7012;

p[1]= -1.6877;

p[2]= -1.6776;

p[3]= -1.6709;

p[4]= -1.6673;

p[5]= -1.6668;

break;

}

case 3:

{

p[0]= -1.6184;

p[1]= -1.5994;

p[2]= -1.5838;

p[3]= -1.5714;

p[4]= -1.5630;

p[5]= -1.5555;

break;

}

case 4:

{

p[0]= -1.5432;

p[1]= -1.5200;

p[2]= -1.5000;

p[3]= -1.4832;

p[4]= -1.4692;

p[5]= -1.4581;

break;

}

case 5:

{

p[0]= -1.4747;

p[1]= -1.4480;

p[2]= -1.4246;

p[3]= -1.4043;

p[4]= -1.3869;

p[5]= -1.3722;

break;

}

}

for (int i=0;i<6;i++)//Вывод p

{

cout<<"p"<<i<<"="<<p[i]<<"n";

}

cout<< "VVEDI S";

//cin>>s;

for (s=0;s<6;s++)

{cout<< "VIBRANO S="<<s<<"n";

float q[6];

for (int i=0;i<6;i++)// Для всех точек f1

{

q[i]=cos((im/5)*(0.7+0.05*s));//im/5 — смена х

im=im++;

}

for (int i=0;i<6;i++)//Вывод q

{

cout<<"q"<<i<<"="<<q[i]<<"n";

}

float m[4];

float k[4];

for (int i=0;i<4;i++)

{

m[i]=( -2+1/(5*p[i]));

k[i]=(1-(h*p[i])+ (h*h*q[i]));

}

for (int i=0;i<4;i++)

{

cout<<"m"<<i<<"="<<m[i]<<"n";

}

for (int i=0;i<4;i++)

{

cout<<"k"<<i<<"="<<k[i]<<"n";

}

float c[4];

float d[4];

c[0]=(a1-(a0*h))/(m[0]*(a1-a0*h)+(k[0]*a1));

d[0]=((k[0]*A*h)/(a1-a0*h) + (2*0*0+2*0-4));/////////////////////////////

for (int i=1;i<4;i++)

{

c[i]=( 1/(m[i]-(k[i]*c[i-1])));

d[i]=(( 2*i*i+2*i-4)*h*h)-(k[i]*c[i-1]*d[i-1]);//////////////////////////////

}

for (int i=0;i<4;i++)

{

cout<<"c"<<i<<"="<<c[i]<<"n";

}

for (int i=0;i<4;i++)

{

cout<<"d"<<i<<"="<<d[i]<<"n";

}

float y[6];

y[5]=(b1*c[3]*d[3]+B*h)/(b1*(1+c[3])+b0*h);

for (int i=3;i>-1;i—)

{

y[i+1]=(c[i]*(d[i]-y[i+2]));

}

y[0]=(a1*y[1]-A*h)/(a1-a0*h);

for (int i=0;i<6;i++)

{

cout<<"y"<<i<<"="<<y[i]<<"n";

}

// fprintf (f, "%c %c %c %c %c %c %c %c %c %c %c %c %c" ,"S","t","Номер fi","t","t","t","t","t","t","t","t","t","n");

fprintf (f, "%i %s %i %s %f %s %f %s %f %s %f %s %f %s %f %s %s" , s,"t", Nom,"t", y[0],"t", y[1],"t",y[2],"t",y[3],"t",y[4],"t", y[5],"t","n");

getch();

}}

getch();

return 0;

}

6. Список библиографических источников:

1. Вычислительная математика в примерах и задачах. /Н. В. Копченова, И. А.Марон.-М.:Гл. ред. физ. –мат. Литературы изд-а Наука, 1972

2. Подготовка научной публикации на персональной ЭВМ. /О. В.Плохих, Издательство ГОУ ВПО УГТУ-УПИ, 2007