Ргр и лабораторные задания по сопромату

Федеральное агентство по образованию

Тверской государственный технический университет

________________________________________________________________

Кафедра сопротивления материалов,

теории упругости и пластичности

СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ

Часть II

Расчетно-проектировочные курсовые

и лабораторные задания

для самостоятельной работы студентов

всех технических специальностей

Тверь 2005

УДК 539. 3/6 (075.8)

ББК 36.91 я 7

Курсовая расчетно-проектировочная работа по дисциплине «Сопротивление материалов» посвящена расчетам на прочность, жесткость и устойчивость элементов конструкций и машин при их статическом и динамическом нагружении.

Она дополнена разделом по экспериментальному исследованию напряженно-деформированного состояния и прочности этих же элементов конструкций, что позволяет студентам оценить надежность теоретических расчетов методами сопротивления материалов.

При разработке курсовой работы частично были использованы и переработаны методические указания по сопротивлению материалов, изданные в 1989 г.(составители В. Н. Лотов, В. В. Гараников, С. А. Кульков с. 15-18, 34-37, 40-41, 49-51) в 1995 г.(составители Н. Л. Охлопков,

М. Ш. Мошкович с. 13-14, 28-32) и в 1999 г.(составители В. Н. Ведерников В. Н. Лотов, В. В. Гараников с. 21-22).

Приложение содержит сортамент прокатной стали.

Преподаватели могут по согласованию с лектором потока сократить число задач в зависимости от реальных условий выполнения ими учебного плана.

Курсовая работа предназначена для студентов строительных, машиностроительных и механических специальностей очной и заочной форм обучения.

Курсовая работа обсуждена на заседании кафедры сопротивления материалов, теории упругости и пластичности и рекомендована к печати (протокол №5 от 16.02.05).

Составители: В. Г. Зубчанинов, В. Н. Ведерников

Под редакцией В. Г. Зубчанинова

© Тверской государственный

технический университет, 2005

3

Содержание курсовой работы

В рамках второй части курса «Сопротивления материалов» каждый студент выполняет пять расчетно-проектировочных работ (РПР) и один

блок лабораторного практикума (табл. 1).

Таблица 1

Содержание и сроки защиты РПР и лабораторного практикума

Оформление курсовой работы

Каждое задание выполняется на листах писчей бумаге формата А 4

(297х210 мм). Образец титульного листа приведен на с. 4.

Защита курсовой работы

Задание выдается в установленные программой сроки. Каждое задание

защищается отдельно. При защите студент должен объяснить ход решения

задания, показать знание теоретического материала и умение применить

его к решению практических задач. Преподаватель ставит дифферен-цированную оценку с учетом сроков защиты и оформления работы в

кафедральном журнале.

Оценки, полученные при защите расчетно-проектировочных, лабора — торных и контрольных работ, а также прилежание студента принимаются во внимание при выставлении итоговой оценки за курсовую работу.

4

Федеральное агентство по образованию

Тверской государственный технический университет

_______________________________________________________________

Кафедра сопротивления материалов,

теории упругости и пластичности

РАСЧЕТНО-ПРОЕКТИРОВОЧНАЯ КУРСОВАЯ РАБОТА ПО КУРСУ «СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ»

Выполнил студент____________________

Вариант____________

Группа_____________

Принял_______________________________________

Тверь 200_

5

Сопротивление материалов (часть II)

Данные ко всем заданиям выдаются преподавателем согласно табл. 2.

Таблица 2

Задание 1. Определение перемещений в балках

методом начальных параметров

Задача 1.1. Для стальной балки с постоянной жесткостью (EJX=const), (рис. 1) требуется:

1. Определить прогиб в т. В и угол поворота сечения в т. С, используя метод начальных параметров.

2. Из условия жесткости │vB│≤[v] подобрать двутавровое поперечное сечение, приняв [v]=0,002L, E=2∙105 МПа.

3. Проверить балку на прочность, если [σ]=160 МПа.

4. Изобразить изогнутую ось балки, используя полученные значения перемещений, условия опирания балки и эпюру изгибающего момента.

Задача 1.2. Аудиторная самостоятельная контрольная работа.

Для стальной балки с постоянной жесткостью (EJX=const),(рис. 2) требуется:

1. Из условия прочности подобрать двутавровое поперечное сечение, если [σ]=160 МПа.

2. Используя метод начальных параметров, определить прогиб в т. В и угол поворота сечения в т. С, если Е=2∙105 МПа.

3. Используя полученные значения перемещений, условия закрепления балки и эпюру изгибающего момента, изобразить изогнутую ось балки.

Задача 1.3. Для деревянной консольной балки круглого ступенчато-переменного сечения (рис. 3) требуется:

6

1.  Построить эпюру прогибов, используя метод начальных параметров.

2. Из условия жесткости │vmax│≤[v] подобрать размеры круглых поперечных сечений, если Е=0,1∙105 МПа, [v]=L/200.

3.  Проверить балку на прочность по нормальным напряжениям и

скалывание вдоль волокон, если [σ]=20 МПа, [τ]=3,6 МПа.

Задача 1.4. Для стальной балки постоянного поперечного сечения (EJX=const), (рис. 4) требуется:

1.  Раскрыть статическую неопределимость балки методом сравнения

перемещений (методом наложения решений).

2.  Построить эпюры внутренних усилий.

3.  Из условия прочности по нормальным напряжениям подобрать двутав-

ровое поперечное сечение, если [σ]=160 МПа.

4.  Определить прогиб в т. В и угол поворота сечения в т. С, принять

E=2∙105 МПа.

Задача 1.5. Используя решение задачи 1.4, определить нагрузку предельного упругого состояния и нагрузку, соответствующую исчерпанию несущей способности, (нагрузку предельного пластического состояния) и резерв прочности балки, если σТР=σТС=240 МПа.

Задание 2. Определение перемещений в балках и стержневых системах энергетическим методом

с использованием формулы Мора

Задача 2.1. Для балки из задачи 1.1 (рис. 1) определить прогиб в т. В и угол поворота сечения в т. С помощью формулы Мора, используя способ Верещагина для вычисления ее интегралов.

Задача 2.2. Аудиторная самостоятельная контрольная работа.

Для балки из задачи 1.2 (рис. 2) определить прогиб в т. В и угол поворота сечения в т. С с помощью формулы Мора, используя способ Верещагина для вычисления ее интегралов.

Задача 2.3. Аудиторная самостоятельная контрольная работа.

Для рамы с постоянной жесткостью участков (EJX=const), (рис. 5) определить вертикальное и горизонтальное перемещение т. В.

Задача 2.4. Для рамы с постоянной жесткостью участков (EJX=const), (рис. 6) определить вертикальное и горизонтальное перемещение т. В.

7

Задача 2.5.* Определить вертикальное перемещение т. В ‌пространственного стального бруса круглого поперечного сечения (рис. 7).

Принять E=2∙105 МПа, G=0,8∙105 МПа.

Задача 2.6.* Определить вертикальное перемещение узла В фермы (рис. 8). Принять EF=const.

Задача 2.7.* Для бруса с круговой осью радиуса R (рис. 9) определить диаметр круглого поперечного сечения из условия жесткости │ΔВВЕР│≤0,001R. Принять E=2∙105 МПа.

Задание 3. Расчет статически неопределимых

балок и рам методом сил

Задача 3.1. Аудиторная самостоятельная контрольная работа.

Для балки (рис. 10) с постоянной жесткостью участков (EJX=const) требуется:

1. Раскрыть статическую неопределимость.

2. Провести деформационную проверку правильности полученного решения.

3. Подобрать двутавровое поперечное сечение, если [σ]=210 МПа.

Задача 3.2. Для балки (рис. 11) с постоянной жесткостью участков (EJX=const) требуется:

1. Раскрыть статическую неопределимость методом сил с рациональным выбором основной системы.

2. Провести деформационную проверку правильности полученного решения.

3. Подобрать поперечное сечение балки в виде двух швеллеров, если [σ]=210 МПа.

4. Определить угол поворота сечения на одной из опор, приняв

E=2∙105 МПа.

Задача 3.3. Для рамы (рис. 12) с постоянной жесткостью участков (EJX=const) требуется:

1. Раскрыть статическую неопределимость и провести деформационную проверку.

2. Проверить прочность рамы, если [σ]=160 МПа и стержни изготовлены из двух швеллеров № .

3. Определить горизонтальное перемещение т. В, если E=2∙105 МПа.

________________________________________________

* Задание выдается по усмотрению преподавателя.

8

Задача 3.4.* Раскрыть статическую неопределимость плоской рамы (рис. 13) с постоянной жесткостью участков (EJX=const). Произвести деформационную проверку. Определить угол поворота сечения в т. С.

Задание 4. Устойчивость и динамика упругих систем

Задача 4.1. Стержень заданного поперечного сечения, закрепленный определенным образом, сжимается силой Р. Требуется:

1. Построить диаграмму критические напряжения~гибкость, используя формулы Эйлера и Энгессера-Шенли:

, ,

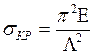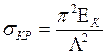где Λ – гибкость стержня; Е – модуль продольной упругости; ЕК – каса-тельный модуль. При построении использовать диаграммы сжатия для стали Ст.3 и алюминиевого сплава Д16Т (дюраль), (табл. 3,4).

Таблица 3

Диаграмма сжатия стали Ст.3

Таблица 4

Диаграмма сжатия сплава Д16Т

9

2. Построить диаграмму допускаемых напряжений на устойчивость~гиб — кость, пользуясь коэффициентом φ из табл. 5 снижения основного допускаемого напряжения [σ]. Принять для стали Ст.3 [σ]=160 МПа, для сплава Д16Т— [σ]=150 МПа.

Таблица 5

Значения коэффициента φ

3. Построить кривую коэффициента запаса на устойчивость .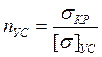

4. Для сравнения построить диаграммы критических напряжений~гибкость по эмпирическим формулам Ф. С. Ясинского

σКР= a – bΛ при Λ0≤Λ≤Λ*,

σКР= σ0 при 0≤ Λ≤Λ0,

и Джонсона

σКР= σ0 – (σ0 – σПЦ)(Λ/Λ*)2 при Λ≤Λ*,

где .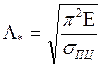

Принять для стали Ст.3 σПЦ=200 МПа, σ0=σТ=240 МПа, E=2∙105 МПа, Λ0=ΛТ=30; для сплава Д16Т – σПЦ=200 МПа, σТ=312 МПа, E=0,75∙105 МПа

σ0=σВ=364 МПа, Λ0=0.

Задача 4.2. Определить допускаемую сжимающую силу Р на стальной стержень, поперечное сечение и схема закрепления которого приведены на рис. 14. При решении использовать таблицу значений коэффициента снижения допускаемого напряжения на сжатие φ для стали Ст.3 (табл. 5). Основное допускаемое напряжение принять [σ]=160 МПа.

10

Задача 4.3. Для сжатого силой Р стального стержня длиной L и заданной формы поперечного сечения (рис. 15) подобрать в соответствии с

методом Ф. С. Ясинского размеры данного сечения. Способы закрепления стержня приведены на рис. 14.

Задача 4.4. Для балки двутаврового поперечного сечения, на которую с высоты h падает груз весом Р (рис. 16), требуется:

1. Определить наибольшее нормальное динамическое напряжение в опасном сечении и динамический прогиб в т. В. Принять E=2∙105 МПа.

2. Определить, как изменится динамическое напряжение при замене правой опоры пружиной с податливостью δ.

Задача 4.5. Для балки (рис. 17) требуется:

1. Определить частоту собственных колебаний системы.

2. Определить область изменения частоты вынужденных колебаний (частоты оборотов машины), при которых возникнут опасные вибрации.

Принять E=2∙105 МПа, сечение балки состоит из прокатных профилей, балку считать невесомой.

Задание 5. Расчеты на прочность

при сложном напряженном состоянии

Задача 5.1. В некоторой частице элемента конструкции (стержня, плиты, балки-стенки, оболочки) задан тензор напряженного состояния

.

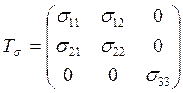Значения напряжений σij заданы на рис. 18. Требуется:

1. Изобразить частицу тела с действующими напряжениями.

2. Определить главные напряжения и направления главных осей и графически изобразить частицу тела с действующими напряжениями.

3. Вычислить среднее напряжение и проверить тождество

I1 = σ11+σ22+σ33 = σ1+σ2+σ3 .

4. Вычислить главные касательные напряжения τij и изобразить их графи-

чески. Проверить равенство

τ13 = τ12+τ23 .

5. Построить круги Мора и найти графически напряжения σν, τν на площадке, наклоненной к главным осям под углом αij= .

6. Вычислить октаэдрическое касательное напряжение и интенсивность напряжений.

11

7. Пользуясь обобщенным законом Гука, вычислить компоненты εij тензора деформированного состояния. Принять E=2∙105 МПа,

G=0,8∙105 МПа, μ=0,25.

8. Вычислить главные деформации, главные сдвиги и сдвиг между октаэдрическими волокнами.

9. Проверить, что главные сдвиги и γокт можно вычислить по формулам

γij = τij/G, γокт = τокт/G.

10. Определить в каком физическом состоянии находится частица тела (упругом, пластическом, разрушенном) по всем теориям прочности. Принять значения пределов текучести и прочности (табл. 6).

Таблица 6

Расчеты провести для всех указанных материалов.

Задача 5.2. Для пространственного стального бруса (рис. 7) подобрать размеры круглого и прямоугольного сечений с отношением сторон h/b= , если [σ]=200 МПа.

Вычислить вертикальное перемещение т. В для бруса круглого поперечного сечения (задача 2.5) при найденном диаметре d.

Задача 5.3. Для вала (рис. 19), изготовленного из стали 45, требуется:

1. Определить крутящий момент на валу по заданной мощности и числу оборотов.

2. Определить окружные, осевые и радиальные усилия, действующие на вал, если D1= м, D2= м.

3. Построить эпюру крутящего момента.

4. Построить эпюры изгибающих моментов от горизонтальных и вертикальных сил.

5. Построить эпюру суммарного изгибающего момента.

6. При помощи эпюр крутящего и суммарного изгибающего моментов найти и вычертить опасное сечение вала, указав на нем опасные точки (частицы).

7. Изобразить напряженное состояние в опасной точке (частице).

8. Подобрать диаметр вала из условий прочности Сен-Венана и Мизеса.

12

Задание 6. Экспериментальные основы исследования

напряженно-деформированного состояния

элементов конструкций

Требуется выполнить лабораторные работы:

Лабораторная работа 6.1. Определение перемещений в балках при поперечном изгибе (определение прогиба в длинной и короткой балках при изгибе).

Лабораторная работа 6.2. Определение перемещений при косом изгибе (экспериментальная проверка формулы для определения перемещений).

Лабораторная работа 6.3. Статически неопределимая балка (экспериментальное определение опорной реакции неразрезной балки).

Лабораторная работа 6.4. Устойчивость сжатого стержня (экспериментальное изучение явления потери устойчивости стержня при

осевом сжатии).

Лабораторная работа 6.5. Концентрация напряжений в полосе с отверстием (экспериментальное определение коэффициента концентрации напряжений у края отверстия).

Лабораторная работа 6.6. Исследование напряженного состояния, возникающего в трубе при изгибе с кручением (экспериментальная проверка теоретических формул для расчета главных напряжений и положения главных площадок).

Лабораторная работа 6.7. Определение динамического коэффициента при ударе (экспериментальное определение динамического коэффициента).

Лабораторная работа 6.8. Исследование колебаний упругой системы с одной степенью свободы (экспериментальное определение частоты собственных колебаний).

58

Библиографический список

Александров А. В., Потапов В. Д., Державин Б. П. Сопротивление ма-

риалов. М.: Высшая школа, 2000. 560 с.

Беляев Н. М. Сборник задач по сопротивлению материалов. М.: Наука, 1972. 348 с.

Зубчанинов В. Г. Сопротивление материалов: Учебное пособие.2-е изд. Тверь: ТГТУ, 2003. Кн.1. 224 с.

Зубчанинов В. Г. Лекции по механике деформируемого твердого тела: В 3 ч. Тверь: ТвеПИ, 1993. 441 с.

Зубчанинов В. Г. Лабораторный практикум по сопротивлению материалов. Калинин: КПИ, 1986. 96 с.

Зубчанинов В. Г., Мошкович М. Ш. Журнал лабораторных работ по курсу сопротивление материалов. Тверь: ТГТУ, 1997. 76 с.

Лабораторный практикум по сопротивлению материалов деформированию. /Под ред. П. М. Огибалова и И. А. Скорого. М.: МГУ, 1961. 197 с.

Писаренко Г. С., Яковлев А. П., Матвеев В. В. Справочник по сопротивлению материалов. Киев: Наук. Думка, 1975. 704 с.

Сопротивление материалов. Лабораторные работы /Под ред. И. А. Цурпала. Киев: Вища школа, 1978. 103 с.

Феодосьев В. И. Сопротивление материалов. М.: Наука, 1974. 559с.;

1986. 512с.

59

Оглавление

Содержание курсовой работы. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3

Оформление курсовой работы. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .3

Защита курсовой работы. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3

Сопротивление материалов (часть II). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5

Задание 1. Определение перемещений в балках

методом начальных параметров. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .5

Задание 2. Определение перемещений в балках и стержневых

системах энергетическим методом с использованием

формулы Мора. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .6

Задание 3. Расчет статически неопределимых

балок и рам методом сил. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7

Задание 4. Устойчивость и динамика упругих систем. . . . . . . . . . . . . 8

Задание 5. Расчеты на прочность при сложном

напряженном состоянии. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10

Задание 6. Экспериментальные основы исследования

напряженно-деформированного состояния

элементов конструкций. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12

Приложения. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .52

1. Уголки стальные горячекатаные равнополочные. . . . . . . . . . . . . . 52

2. Уголки стальные горячекатаные неравнополочные. . . . . . . . . . . . 54

3. Двутавры стальные горячекатаные. . . . . . . . . . . . . . . . . . . . . . . . . .56

4. Швеллеры стальные горячекатаные. . . . . . . . . . . . . . . . . . . . . . . . . 57

Библиографический список. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 58

СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ

Часть II

Расчетно-проектировочные курсовые

и лабораторные задания

для самостоятельной работы студентов

всех технических специальностей

Составители: В. Г. Зубчанинов, В. Н. Ведерников

Под редакцией В. Г. Зубчанинова

Редактор Е. В. Маняшина

Технический редактор Г. В. Комарова

Подписано к печати

Формат 60 х 84/16 Бумага писчая

Физ. печ. л. 3,75 Усл. печ. л. 3,49 Уч.-изд. л. 3,26

Тираж 200 экз. Заказ № Цена

Издательство ТГТУ