Шпаргалка по теоретической механике
|
Билет №1. Статика – раздел механики, изучающий условия равновесия материальных тел, находящихся под действием сил. Абсолютно твердое тело – тело, расстояние между двумя точками которого всегда остается постоянным. Свободное тело – тело, перемещение в пространстве которого, ничем не ограничено. Несвободное тело – тело, перемещение в пространстве которого ограничено другими телами. Сила – мера механического воздействия одного тела на другое. Параметры, определяющие действие силы на твердое тело. Сила задается модулем, направлением и точкой приложения. Обозначается большими буквами латинского алфавита: Размерность сил. Основной единицей измерения силы в СИ является 1 ньютон (Н) или 1 килоньютон (кН). 1кН = 1000Н. Линия действия силы – линия, вдоль которой действует сила. Внешние силы – силы, которые действуют на тело со стороны других тел (не входящих в систему). Внутренние силы – силы, с которыми части данного тела дей-ствуют друг на друга. Сосредоточенная сила – сила, приложенная к телу какой-нибудь его точке. Распределенная сила – сила, действующая на все точки данного объема, данной части поверхности тела или линии. |
Билет №2. Система сил — совокупность нескольких сил, действующих на твердое тело. Виды систем сил: -Плоская система сил – совокупность сил, линии действия кото-рых лежат в одной плоскости. -Пространственная система сил – совокупность сил, линии действия которых не лежат одной плоскости. -Сходящееся система сил — совокупность сил, линии действия которых пересекаются одной точке. -Параллельная система сил – совокупность сил, линии действия которых параллельны друг другу. -Эквивалентная система сил – совокупность сил, при котором одну систему сил, можно заменить другой, не изменяя при этом покоя или движения, в которых находится тело. -Уравновешенная система сил – совокупность сил, под действи-ем которых свободное твердое тело может находится в покое. Равнодействующая сила – совокупность сил, при которой одна система сил эквивалентна другой. Задачи статики: Первая задача статики. Преобразование систем сил, действую-щих на твердое тело, системы им эквивалентные относительно некоторого центра О. Вторая задача статики. О равновесие: каким условиям должна удовлетворять система сил, приложенная к данному телу, чтобы она была уравновешенной? |
Билет №3. Аксиомы статики. 1.аксиома двух сил. Две силы, действующие на свободное твердое тело, являются уравновешенными тогда и только тогда, когда эти силы равны по модулю и действуют вдоль одной прямой в противоположные стороны. 2.аксиома присоединения. Действие данной системы сил на абсолютно твердое тело не изменяется, если прибавить к ней или отнять от нее уравновешенную систему сил: ( 3.аксиома параллелограмма. Система двух сил, приложенных к телу в одной точке, равна их геометрической сумме 4.аксиома равенства действия и противодействия. Всякому действию одного тела на другое составляет равное по величине, но противоположное по направлению противодействие. 5.аксиома отвердевания. Если деформируемое тело под действием системы сил находится в равновесии, то при отвердевании его равновесие сохраняется. |
|
Билет №4. Связи – тела, ограничивающие перемещение тела. Реакция связи – сила, с которой данная связь действует на тело, препятствуя тем или иным его перемещениям. Реакция связи направлена в противоположную сторону действия силы. Основные виды связей: 1.Гладкая поверхность (без трения). Реакция гладкой поверхности направлена по нормали к этой поверхности (перпендикулярна общей касательной). 2.Опорная точка. Реакция перпендикулярна опирающейся поверхности. 3.Идеальная нить (гибкая, невесомая, нерастяжимая). Моделирует трос, канат, цепь, ремень, … . Реакция идеальной нити направлена по нити к точке подвеса. 4.Идеальный стержень (жесткий, невесомый стержень, на концах которого шарниры). Реакция связи направлена по стержню. В отличие от нити стержень может работать на сжатие. 5.Цилиндрический шарнир. Такая связь позволяет телу перемещаться вдоль оси, поворачиваться вдоль оси шарнира, но не позволяет точке закрепления перемещаться в плоскости, перпендикулярной оси шарнира, и проходит через нее. 6.Сферический шарнир. Такая связь не дает точке тела переме-щаться ни в одном из направлений. Положение реакции не опре- |
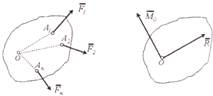
Билет №5. Сложение двух сил. Геометрическая сумма
Или построением силового треугольника:
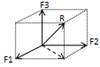
Модуль силы Сложение трех сил, не лежащих в одной плоскости. Геометрическая сумма
Сложение системы сил. Сложение системы сил сводится к нахождению ее главного век-тора. |
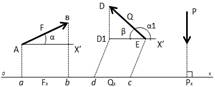
Билет №6. Проекция силы на ось. Проекция силы на ось – алгебраическая величина, равная произ-ведению модуля силы на косинус угла между силой и положи-тельным направлением оси:
Fx = F · cosα = ab, Qx = Q · cosα1 = — Q · cosβ = — dc,
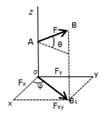
Проекция силы на плоскость. Проекция силы Модуль I В некоторых случаях для нахождения проекции силы на ось удобно найти сначала ее проекцию на плоскость, а затем найденную проекцию на плос- |
|
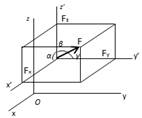
Билет №7. Аналитический способ задания силы. Для того, чтобы задать силу аналитически, достаточно задать ее проекции на оси системы координат. Пространственная система координат. Если заданы проекции Fx, Fy, Fz, то модуль силы определяется по формуле: I Направление силы находится че-рез вычисление углов α, β, γ с по-мощью направляющих косинусов: cosα = Fx/F, cosβ = Fy/F, cosγ = Fz/F
Плоская система координат. Если заданы проекции Fx, Fy,то модуль и направление силы определяется по фор-мулам: I α = arccos(Fx/F). Аналитический способ сложения сил. Аналитический способ сложения сил базируется на теореме геометрии: Теорема. Проекция вектора суммы на какую-нибудь ось равна ал-гебраической сумме проекций слагаемых векторов на ту же ось. |
Билет №8. Равновесие сходящейся системы сил. Геометрические условия равновесия сходящейся системы сил.
Равнодействующая Таким образом при равновесии: R = Так как Аналитические условия равновесия сходящийся системы сил. Пространственная система сходящихся сил. Для равновесия пространственной системы сходящихся сил необ-ходимо, чтобы сумма проекций этих сил на каждую из трех коор-динат осей была равна нулю: Эти условия называются аналитические условия равновесия пространственной сходящейся системы сил. Плоская система сходящихся сил. Для равновесия плоской сходящейся системы сил необходимо, |
Билет №9. Виды моментов сил. -алгебраический момент силы относительно центра; -векторный момент силы относительно центра; -момент силы относительно оси. Алгебраический момент силы относительно цен-тра – скалярная величии-на, равная произведению модуля силы на ее плечо: mO(
Плечо силы (h) – кратчайшее расстояние от моментальной точки до линии действия силы. Если сила поворачивает тело относительно точки против часовой стрелки, то знак момента «+» и наоборот – «-». Алгебраический момент силы относительно центра равен нулю если: -модуль силы равен нулю; -линия действия силы проходит через моментальную точку. Теорема Вариньона для плоской системы сил. Если данная система сил имеет равнодействующую, то ее момент Относительно центра О равен алгебраической сумме моментов сил системы относительно того же центра: |
|
Билет №10. Пара сил. Плоская система пар. Пара сил – система дух равных по модулю, параллельных и нап-равленных в противоположные стороны сил, дейстующих на абсолютно твердое тело. Пара сил не имеет равнодействующей. Плоскость, в которой действует пара сил, называется плоскостью действия пары. Виды моментов пары сил. -векторный момент; -алгебраический момент. Алгебраический момент пары сил. Алгебраический момент пары сил – взятое с соответствующим знаком произведение модуля одной из сил пары на плечо пары: m = ± F · d. Свойства пары сил. -пару, не изменяя оказываемого ею на твердое тело действия, можно переносить куда угодно в плоскости действия пары; -пару, не изменяя оказываемого ею на твердое тело действия, можно переносить из данной плоскости в любую другую плос-кость; -действие пары сил на твердое тело полностью характеризуется ее моментом, модуль которого равен m = ± F · d. Теорема о сложении пар, лежащих одной плоскости. Система пар, лежащих в одной плоскости и действующих на абсо-лютно твердое тело, эквивалентна одной паре с моментом, рав — |
Билет №11. Приведение произвольной плоской системы сил к неподвиж-ному центру (1-задача статики). Случаи приведения сил: -приведение произвольной пространственной системы сил; -приведение произвольной плоской системы сил. Главный момент произвольной плоской системы сил. Величина Mo равная алгебраической сумме моментов всех сил относительно неподвижного центра О, называется главным моментом произвольной плоской системы сил относительно данного центра: Mo =∑mo( Теорема о приведении плоской системы сил. Любая произвольная система сил, действующая на твердое тело, при приведении к произвольно выбранному центру О заменяется одной силой |
Билет №12. Условия равновесия произвольной плоской системы сил. Геометрические условия равновесия. Для равновесия произвольной плоской системы сил необходимо, чтобы главный вектор этой системы сил и ее главный момент относительно любого центра были равны нулю:
Основная форма аналитических условий равновесия произволь-ной плоской системы сил. Для равновесия произвольной плоской системы сил необходимо, чтобы сумма всех сил на каждую из двух координатных осей и сумма их моментов относительно любого центра, лежащего в плоскости действия сил, были равны нулю:
Первая вспомогательная форма аналитических условий равно-весия произвольной плоской системы сил. Для равновесия произвольной плоской системы сил необходимо, чтобы сумма моментов всех этих сил относительно каких-нибудь центров А и В и сумма их проекций на ось Оx, не перпендикуляр-ную прямой АВ, были равны нулю:
Аналитические условия равновесия плоской системы парал-лельных сил. Если все силы параллельны какой-нибудь оси, то аналитические условия равновесия системы сил имеют вид: |
|
Распределенные нагрузки характеризуются интенсивностью [q] (Н/м). Виды распределенной по линии нагрузки (силы). Равномерно распределенная нагрузка – заменяется сосредото-ченной силой Q = q · l, приложенной к середине участка. Распределенная по линейному закону – заменяется сосредото-ченной силой Q = q · l/2, приложенной на расстоянии 1/3 от конца участка распределения. Распределенная по произвольному закону – заменяется сосредо-точенной силой Q = ∫q(x)dx, приложенной в центре тяжести С фигуры. |
||
|
кость спроектировать: Fx = Fxy · cosϕ= F · cosθ · cosϕ, Fy = Fxy · sinϕ= F · cosθ · sinϕ. Иногда для нахождения проекции силы на ось удобно применять прямое проектирование: Fx = F · cosα, Fy = F · cosβ, Fz =F · cosγ.
|
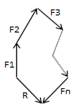
Главный вектор – геометрическая сумма всех сил, входящих в систему: Главный вектор можно найти посредством построения многоу-гольника, который строится посредством параллельного переноса сил. При этом каждая последующая сила откладывается в масшта-бе от конца предыдущей силы:
Разложение силы по двум заданным направлениям. Для разложения силы Разложение силы по трем заданным направлениям. Для разложения силы |
делено, но она может быть представлена тремя взаимно перпендикулярными составляющими. 7.Жесткая заделка. Такая связь препятствует перемещению и повороту вокруг точки закрепления. Контакт тела со связью осуществляется по поверхности. Имеем распределенную систему сил реакции, которая может быть заменена одной силой и парой сил. Аксиома освобождаемости связей. Всякое несвободное тело можно считать свободным, если мысленно освободится от связей, а их действие заменить соответствующими реакциями. |
|
mo(
Если равнодействующие двух сил |
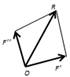
Теорема о трех силах. Теорема. Если твердое тело находит-ся в равновесии под действием трех сил, лежащих в одной плоскости, то линии действия этих сил пересекают-ся в одной точке. |
Сложение пространственной системы сил. Пусть силы
Согласно теореме (Проекция вектора суммы на какую-нибудь ось равна алгебраической сумме проекций слагаемых векторов на ту же ось) если Rx = I Направление равнодействующей силы находится через вычис-ление углов α, β, γ с помощью направляющих косинусов: cosα = Rx/IRI, cosβ = Ry/IRI, cosγ = Rz/IRI и α = arccos(Rx/IRI), β = arccos(Ry/IRI), γ = arccos(Rz/IRI). Сложение плоской системы сил. Пусть силы
Согласно теореме (Проекция вектора суммы на какую-нибудь ось равна алгебраической сумме проекций слагаемых векторов на ту же ось) если Rx = Модуль и направление
|
|
или
|
ным алгебраической сумме моментов складываемых пар: M = m1 + m2 + … + mn = ∑mk. Условия равновесия системы пар, лежащих в одной плоскости. Система пар, лежащих в одной плоскости и действующих на абсолютно твердое тело, эквивалентна нулю (находится в равновесии), если алгебраическая сумма моментов пар равна нулю: ∑mk = 0. |
|
|
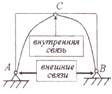
Билет №13. Условия равновесия произвольной плоской системы сил, прило-женнойй к двум абсолютно твердым телам. Внешние и внутренние связи. Внутренние связи – связи, соединяющие части конструкции, а связи, присоединяющие ее к другим телам – внешние.
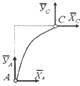
Метод замораживания. При определении реакций внешних связей составляют одну из форм условий равновесия для «замороженной» конструкции АВС:
Однако этих условий равновесия не доста-точно для определения всех реакций вне-шних связей (4 реакции невозможно оп-ределить из 3-х уравнений). Такие системы называются статически неопределимые.
|
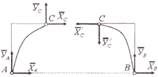
Билет №14. Определение центра тяжести.
Координаты центра тяжести неоднородного тела. Координаты центра тяжести определяются по формулам: ХС = где
Координаты центра тяжести однородных тел. Однородное тело – тело, вес одной из его части которого пропорционален объему этой части: pk = γ · Vk , а вес Р всего тела пропорционален объему V: Р = γ · V, где γ – вес единицы объема. Центр тяжести объема V. Координаты центра тяжести площади определяются по формулам ХС = где наты объемов частиц тела. |
Билет №15. Способы определения координат центров тяжести однород-ных тел. Способ симметрии. Если однородное тело имеет плоскость, ось или центр симметрии, то его центр тяжести лежит соответственно или в плоскости симметрии, или на оси симметрии, или в центре симметрии. Из свойств симметрии следует, что центр тяжести однородного кольца, круглой или прямоугольной пластины, прямоугольного параллелепипеда, шара и других однородных тел, имеющих центр симметрии, лежит в геометрическом центре этих сил. Способ разбиения. Суть метода разбиения заключается в том, что если тело можно разбить на конечное число таких частей, для каждой из которых положение центра тяжести известно, то координаты центра тяжести можно вычислить по формулам: ХС = Способ дополнения. Этот способ является частным случаем способа разбиения. Он применяется к телам, имеющих вырезы, если центры тяжести тел без выреза и вырезной части известны. При этом площади вырезанных частей принимаются отрицательными. Способ интегрирования. Способ заключается в том, что суммы в формулах заменяют интегралами: |
|
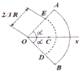
Билет №16. Центры тяжести однородных тел. Центр тяжести дуги окружности. Центр тяжести дуги окружности, радиусов R опирающейся на угол 2α имеет координаты: xC = (R · sinα)/α, y C = 0.
Центр тяжести площади треугольника. Центр тяжести треугольника лежит на пересечении его медиан.
Центр тяжести кругового сектора. Центр тяжести кругового сектора лежит на его оси симметрии на расстоянии от центра О равном: xC = (2R · sinα)/3α.
|
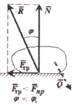
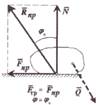
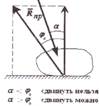
Билет №17. Трение. Основные виды трения: трение скольжения и трение качения. Сила трения скольжения – сила сопротивления относительному скольжению при стремлении двигать одно тело по поверхности другого в плоскости сопротивления тел.
Законы трения скольжения. 1.При стремлении сдвинуть одон тело по поверхности другого в плоскости соприкосновения тел возникает сила трения. 2.Сила трения приложенная к телу, направлена в противополож-ную сторону силам, которые стремятся сдвинуть тело. 3.Предельная сила трения равна произведению статического коэффициента трения на нормальную реакцию: Fпр = f0 · N. Трение скольжение при движении. При движении сила трения скольжения направлена в сторону, противоположную движению, и равна произведению динамичес-кого коэффициента трения на нормальную реакцию: F = f · N. Реакция шероховатой связи. Угол трения – наибольший угол ϕ0, который полная реакция шероховатой связи образует с нормалью к поверхности: tgϕ0 = Fпр/N = f0. |
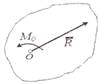
Билет №18. Векторный момент силы относительно центра.
Момент силы относительно оси. Проекция момента силы относи-тельно центра, на какую-нибудь ось, проходящую через центр, называется моментом силы относительно оси: Векторный момент пары сил. Векторный момент пары сил – это вектор, модуль которого равен произведению модуля одной из сил пары на ее плечо: m = F · d, и который направлен перпендикулярно плоскости действия пары в ту сторону, откуда пара видна стремящейся повернуть тело против хода часовой стрелки. Свойства векторного момента пары сил. 1.действие пары сил на твердое тело полностью характеризуется |
|
Билет №19. Теорема Пуансо. Любая система сил, действующих на абсолютно твердое тело, при приведении к произвольно выбранному центру О заменяется одной силой
Следствие из теоремы Пуансо. Две системы сил, имеющие одинаковые главные векторы и глав-ные моменты относительно одного и того же центра, эквива-лентны. Частные случаи приведения системы сил к центру. 1.Если для данной системы сил 2.Если для данной системы сил |
Билет №20. Геометрические условия равновесия произвольной простран-ственной системы сил. Для равновесия любой системы сил необходимо, чтобы главный вектор этой системы сил и ее главный момент относительно любого центра были равны нулю: Модули главного вектора. I Модуль главного момента. I Теорема Вариньона о моменте равнодействующей. Если данная система сил имеет равнодействующую, то момент равнодействующей относительно любого центра равен сумме моментов сил системы относительно того же центра: mo( Равновесие пространственной системы параллельных сил. Если все действующие силы параллельны друг другу, то можно выбрать оси координат так, что ось Оz будет параллельна силам. Тогда из шести уравнений равновесия останутся только три:
|
|
|
ХС = где
Экспериментальный способ. Различают два способа определения положения центра тяжести однородных и неоднородных тел произвольной формы: -метод подвешивания. Заключается в том, что тело подвешивают на нити или тросе за различные его точки. Направление нити, на которой подвешено тело будет каждый раз давать направление силы тяжести. Точка пересечения этих линий даст положение центра тяжести тела. -метод взвешивания. Заключается в том, что одну из реакций опор тяжелого неодно-родного тела произвольной конфигурации определяют посред-ством взвешивания на специальных весах, а другую реакцию находят из уравнений равновесия. |
Центр тяжести площади S. Координаты центра тяжести площади определяются по формулам ХС = где Центр тяжести линии L. Координаты центра тяжести линии определяются по формулам ХС = где наты частиц линии. |
частей конструкции (АС или ВС), расчленяя ее на части по внутрен-ней связи. При этом, как правило, необходимо составить уравнение моментов, принимая за моментную тоску ту точку, где тела соединяются связью (на рисунке т. С): Метод разбиения. При определении реакций внешних связей и внутренних связей конструкцию расчленяют по внутреннему шарниру, и для каждой части составляют уравнения равновесия.
Для части АС: Для части ВС: С учетом того, что Для проверки правильности решения могут быть составлены уравнения равновесия для «замороженной» конструкции. |
|
ее векторным моментом. 2.Две пары сил, имеющие одинаковые векторные моменты экви-валентны. 3.Векторный момент можно приложить в любой точке, то есть этот вектор свободный. Теоремы о сложении пар сил, не лежащих в одной плоскости. Теорема1. Действие на твердое тело двух пар с моментами Теорема2. Система пар, действующих на тело, эквивалентна одной паре с моментом, равным геометрической сумме моментов складыва-емых пар: Геометрические условие равновесия системы пар. При равновесии систем пар момент равнодействующей пары будет равен нулю: Аналитические условия равновесия системы пар. В проекциях на оси координат векторное равенство где
|
Трение качения. Трение качения – сопротивление, возникающее при качении од-ного тела по поверхности другого. Трение качения возникает из-за деформации соприкасающихся тел. |
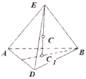
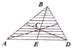
Центр тяжести объема пирамиды. Центр тяжести пирамиды С лежит на прямой С1Е, где С1 – центр тяжести площади основания пирамиды.
|
А
Абсолютно твердое тело (1)
Аксиомы статики (3)
Аксиома освобождаемости связей (4)
Алгебраический момент пары сил (10)
Алгебраический момент силы относительно центра (9)
Аналитический способ задания силы (7)
Аналитический способ сложения сил (7)
Аналитические условия равновесия системы пар (18)
Аналитические условия равновесия плоской системы параллельных сил (12)
Аналитические условия равновесия сходящийся системы сил (8)
В
Векторный момент пары сил (18)
Векторный момент силы относительно центра (18)
Виды моментов сил (9)
Виды моментов пары сил (10)
Виды связей (4)
Внешние силы (1)
Внутренние силы (1)
Внешние и внутренние связи (13)
Г
Геометрические условия равновесия произвольной пространственной системы сил (20)
Геометрические условия равновесия сходящейся системы сил (8)
Геометрические условие равновесия системы пар (18)
Главный вектор (5)
Главный момент произвольной плоской системы сил (11)
З
Задачи статики (2)
Законы трения скольжения (17)
К
Координаты центра тяжести однородных тел (14)
Координаты центра тяжести неоднородного тела (14)
Л
Линия действия силы (1)
М
Метод замораживания (13)
Метод разбиения (13)
Модули главного вектора (20)
Модуль главного момента (20)
Модуль силы (5)
Момент силы относительно оси (18)
Моментальная точка (9)
Н
Несвободное тело (1)
О
Однородное тело (14)
Основная форма аналитических условий равновесия произвольной плоской системы сил (12)
П
Пара сил (10)
Параметры, определяющие действие силы на твердое тело (1)
Первая вспомогательная форма аналитических условий равновесия произвольной плоской системы сил (12)
Первая задача статики (11)
Плоская система координат (7)
Параллельная система сил (2)
Плечо силы (9)
Плоская система сил (2,8)
Плоская система пар (10)
Плоская система сходящихся сил (8)
Приведение произвольной плоской системы сил к неподвижному центру (11)
Проекция силы на ось (6)
Проекция силы на плоскость (6)
Пространственная система координат (7)
Пространственная система сил (2,7)
Пространственная система сходящихся сил (8)
Р
Равнодействующая сила (2,8)
Равновесие пространственной системы параллельных сил (20)
Равновесие сходящейся системы сил (8)
Равномерно распределенная нагрузка (1)
Разложение силы по двум заданным направлениям (5)
Разложение силы по трем заданным направлениям (5)
Размерность сил (1)
Распределенная сила (1)
Реакция связи (3)
Реакция шероховатой связи (17)
С
Свободное тело (1)
Свойства векторного момента пары сил (18)
Свойства пары сил (10)
Связи (3)
Сила (1)
Сила трения скольжения (17)
Система сил (2,5,7)
Система координат (7)
Сложение двух сил (5)
Сложение плоской системы сил (7)
Сложение пространственной системы сил (7)
Сложение системы сил (5)
Сложение трех сил, не лежащих в одной плоскости (5)
Сосредоточенная сила (1)
Способ симметрии (15)
Способ разбиения (15)
Способ дополнения (15)
Способ интегрирования (15)
Способы определения координат центров тяжести однородных тел (15)
Статика (1)
Статически неопределимые системы (13)
Сходящееся система сил (2,8)
Т
Теорема Вариньона для плоской системы сил (9)
Теорема Вариньона для плоской системы сил (случай двух сил) (9)
Теорема Вариньона о моменте равнодействующей (20)
Теорема Пуансо (19)
Теорема о приведении плоской системы сил (11)
Теоремы о сложении пар сил, не лежащих в одной плоскости (18)
Теорема о трех силах (8)
Теорема о сложении пар, лежащих одной плоскости (10)
Трение (17)
Трение качения (17)
Трение скольжение при движении (17)
У
Угол трения (17)
Уравновешенная система сил (2)
Условия равновесия произвольной плоской системы сил (12)
Условия равновесия произвольной плоской системы сил, приложенной к двум абсолютно твердым телам (13)
Условия равновесия системы пар, лежащих в одной плоскости (10)
Ц
Центр тяжести (14)
Центр тяжести объема V (14)
Центр тяжести площади S (14)
Центр тяжести линии L (14)
Центры тяжести однородных тел (16)
Центр тяжести дуги окружности (16)
Центр тяжести площади треугольника (16)
Центр тяжести кругового сектора (16)
Центр тяжести объема пирамиды (16)
Ч
Частные случаи приведения системы сил к центру (19)
Э
Эквивалентная система сил (2)
 Px = 0.
Px = 0.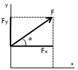
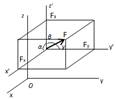 и α = arccos(Fx/F), β = arccos(Fy/F), γ = arccos(Fz/F).
и α = arccos(Fx/F), β = arccos(Fy/F), γ = arccos(Fz/F).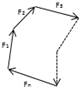 Сходящаяся система сил
Сходящаяся система сил 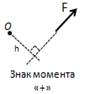
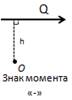 Центр О относительно которого вычисляется ал-гебраический момент, называется моментальной точкой.
Центр О относительно которого вычисляется ал-гебраический момент, называется моментальной точкой. 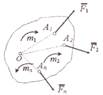
 Теорема Вариньона для плоской системы сил (случай двух сил).
Теорема Вариньона для плоской системы сил (случай двух сил).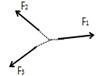 чтобы сумма проекций этих сил на каждую из двух координатных осей была равна нулю:
чтобы сумма проекций этих сил на каждую из двух координатных осей была равна нулю: 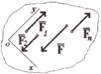
 Такую статическую неопределимость рас-крывают составлением дополнительного уравнения(ий) равновесия для одной из
Такую статическую неопределимость рас-крывают составлением дополнительного уравнения(ий) равновесия для одной из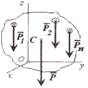 Центр тяжести – точка (на рисунке С), связанная с телом, через которую проходит линия действия равнодей-ствующей сил тяжести, действующих на частицы данного тела, при любом положении тела.
Центр тяжести – точка (на рисунке С), связанная с телом, через которую проходит линия действия равнодей-ствующей сил тяжести, действующих на частицы данного тела, при любом положении тела.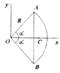
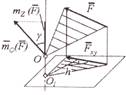
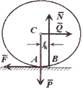 Векторный момент силы относительно центра – это приложенный в центре вектор, модуль которого равен произве-дению модуля силы на ее плечо и который направлен перпендикулярно плоскости, проходящей через центр и силу, в ту сторону, откуда сила видна стремящейся повернуть тело вокруг центра против хода часовой стрелки: I
Векторный момент силы относительно центра – это приложенный в центре вектор, модуль которого равен произве-дению модуля силы на ее плечо и который направлен перпендикулярно плоскости, проходящей через центр и силу, в ту сторону, откуда сила видна стремящейся повернуть тело вокруг центра против хода часовой стрелки: I