Сила гидростатического давления на плоские поверхности

Рис.3.11 Рис.3.12

Согласно уравнению гидростатики атмосферное давление передается равномерно по всей глубине h, а давление от столба жидкости — по линейному закону: p = γh. Так как сосуд окружает среда с атмосферным давлением, то действие атмосферного давления через жидкость на стенки компенсируется давлением извне, т. е. силовое воздействие на стенки сосуда окажет только давление столба жидкости.

Гидростатическое давление направлено по нормали к стенкам сосуда согласно его свойству.

2. Сосуд с вертикальными плоскими стенками заполнен жидкостью, на поверхности которой создано избыточное давление ро (рис.3.12). В этом случае силовое воздействие на стенки оказывает как избыточное давление на поверхности, так и давление от столба жидкости.

3. Сосуд с наклонной плоской поверхностью, открытый сверху (рис.3.13).

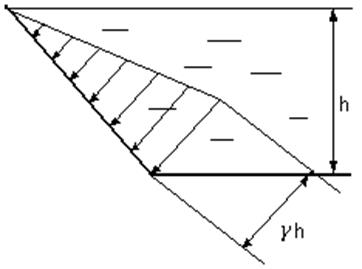
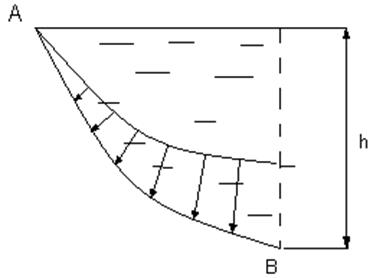
Рис.3.13 рис.3.14

Построение эпюры аналогично предыдущим случаям.

4. Сосуд, стенка (стенки) которого имеет криволинейную поверхность, например АВ (рис.3.14).

Для построения эпюры гидростатического давления, действующего на поверхность АВ, необходимо через определенный интервал по глубине h провести касательные плоскости к кривизне поверхности и к ним по нормали линии действия давления. Закон изменения давления в этом случае повторит форму криволинейной поверхности.

3.4. Сила гидростатического давления на плоские поверхности

Давление, созданное в жидкости, действуя на поверхности различных устройств и их элементов, создает силу. Плоскими поверхностями могут быть стенки различных резервуаров, тела плотин, клапаны, щиты и затворы.

Определим величину силы, действующей на плоскую поверхность, и точку ее приложения.

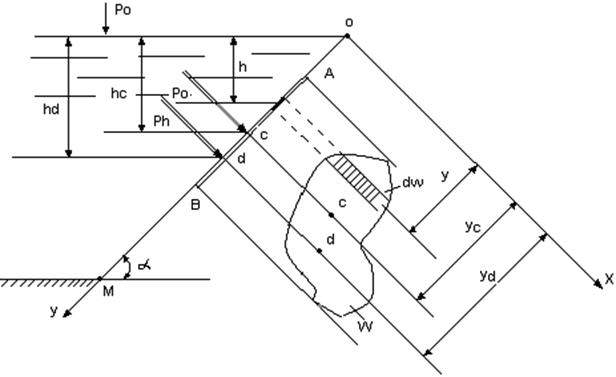
Рис.3.15

Представим (рис.3.15) сосуд, наполненный жидкостью и имеющий плоскую стенку ОМ под углом α к горизонту. В плоскости этой стенки наметим оси координат ОУ и ОХ. Ось ОХ направим перпендикулярно к плоскости чертежа.

На стенке сосуда наметим некоторую плоскую фигуру АВ любого очертания, имеющую площадь w. Из точки О проведем ось ОХ, нормальную к направлению АВ, т. е. ось ОХ совместим с плоскостью чертежа. Будем мысленно вращать фигуру АВ вокруг оси ОУ так, чтобы эта фигура совместилась с плоскостью чертежа.

Выделим на площади фигуры бесконечно малую поверхность в виде полоски dw, погруженную на глубину h. При этом расстояние полоски от оси ОХ равно y. гидростатическое давление в области бесконечно малой плоскости согласно основному уравнению гидростатики будет

.

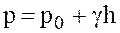Тогда сила давления на элементарную площадку

. (3.16)

Интегрируя выражение (3.16) в пределах площади ω и заменив h = у·sinα, получим

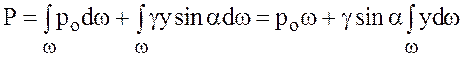. (3.17)

Интеграл 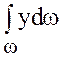представляет собой статический момент площади фигуры АВ относительно оси ОХ. Из механики известно, что

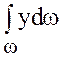= yсw, (3.18)

где ус – расстояние центра тяжести площади фигуры АВ относительно оси ОХ.

Подставив (3.18) в (3.17) и заменив ycsinα = hc, получим силу, действующую на площадь ω:

(3.19)

Это означает, что сила давления P жидкости на плоскую фигуру, погруженную в жидкость, равна произведению этой площади ω на гидростатическое давление в ее центре тяжести (po+γhc).

Из формулы (3.19) следует, что сила Р состоит из двух сил: силы роω и силы γhсω. Сила pоω создает равномерную нагрузку и приложена в центре тяжести фигуры площадью ω. Сила γhсω создает неравномерную нагрузку и поэтому точка ее приложения не совпадает с центром тяжести фигуры. Эта точка называется центром гидростатического давления; обозначается она буквой d. Для нахождения точки приложения силы γhсω применим теорему механики о моменте равнодействующей силы: момент равнодействующей силы относительно оси ОХ равен сумме моментов от элементарных сил:

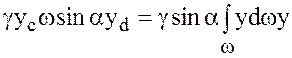. (3.20)

Интеграл 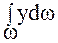представляет собой момент инерции Ix площади ω относительно оси ОХ. Из механики известно, что

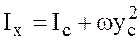, (3.21)

где Ic — момент инерции площади относительно оси ОХ, проходящей через центр тяжести.

Подставим выражение (3.21) в (3.20):

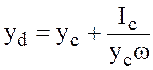. (3.22)

Из выражения (3.22) следует, что центр гидростатического давления yd находится ниже центра тяжести на величину эксцентриситета .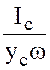

3.5. Сила гидростатического давления, действующая

на криволинейные поверхности

В технике, в частности машиностроении, приходится встречаться как с простыми, так и со сложными криволинейными поверхностями, подверженными гидростатическому давлению (сферические крышки резервуаров, стенки круглых трубопроводов, цилиндрических баков, цистерн и т. д.).

Если при определении силы полного гидростатического давления, действующего на плоские фигуры, по существу производится простое сложение параллельных сил, то при решении аналогичной задачи для криволинейных поверхностей приходится суммировать силы, имеющие различные направления. Это обстоятельство значительно усложняет задачу, требуя применения специальных расчетных приемов.

Принцип, положенный в основу существующих решений, заключается в определении составляющих сил полного гидростатического давления по нескольким направлениям, с последующим геометрическим сложением этих частных сил.

Рассмотрим криволинейную поверхность АВ, подверженную действию избыточного гидростатического давления только от столба жидкости (рис.3.16).

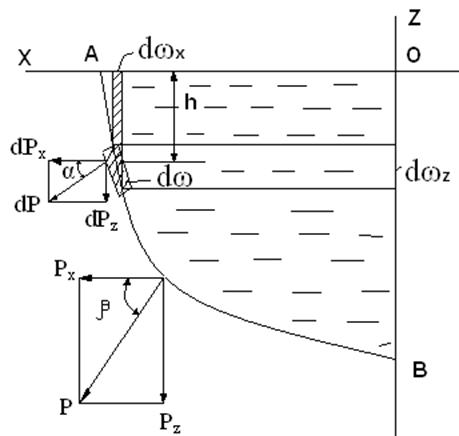
Рис.3.16

Выделим на этой поверхности бесконечно малую полоску площадью dω, центр тяжести которой погружен в жидкости на глубину h. На эту элементарную полоску нормально к криволинейной поверхности действовует сила dР=γhdω, которую можно разложить на горизонтальную и вертикальную составляющие: dРх и dРz. Сила dР наклонена к горизонту под углом α. Тогда

dРх=dР·cosα, dРz =dР·sinα,

или dРх=γhdω·cosα; dРz = γhdω ·sinα.

Из рисунка видно, что dω·cosα является площадью проекции элементарной полоски dω на вертикальную плоскость, т. е. dω·cosα = dωz. следовательно, dРх= γhdωz.

Тогда горизонтальная составляющая силы избыточного давления на рассматриваемую криволинейную поверхность

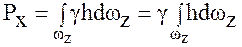
Здесь 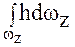является статическим моментом всей площади вертикальной проекции криволинейной поверхности ωz относительно свободной поверхности жидкости, совпадающей с осью ОХ: .

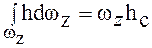Таким образом

Рх= γhc ωz. (3.23)

Другими словами, горизонтальная составляющая Рх выражается произведением площади проекции криволинейной фигуры на вертикальную плоскость на гидростатическое давление в центре тяжести этой площади.

Точка ее приложения, т. е. расстояние от свободной поверхности до центра давления определяется аналогично, как и для плоской поверхности.