Сила лоренца

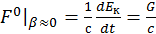(2.1.25)

Таким образом, величина имеет размерность и смысл мощности:

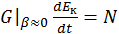(2.1.26)

К этому соотношению можно подойти с другой стороны, используя ортогональность четырехмерных векторов скорости и ускорения:

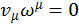. (2.1.27)

Домножая (2.1.27) на m2, получим:

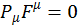. (2.1.28)

То есть вектора и также ортогональны в четырехмерном пространстве.

§ 2.2. Сила Лоренца

Сила Лоренца – сила, действующая на заряд, движущийся в электромагнитном поле. Рассмотрим силу Лоренца как следствие преобразования Лоренца.

Как известно, сила, действующая на заряд в системе покоя имеет вид:

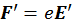(2.2.1)

Это соотношение переведем в лабораторную систему с помощью преобразования Лоренца. Будем использовать общие преобразования Лоренца:

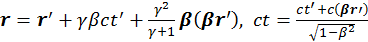(2.2.2)

Здесь β- скорость частицы в лабораторной системе.
Произведем в формуле (2.2.2) замену r→F и учтем, что F— пространственно подобный вектор. Следуя этим рассуждениям, получим:

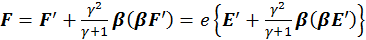(2.2.3)

Для нахождения E′ через поля в лабораторной системе воспользуемся преобразованиями Лоренца для напряженности полей:

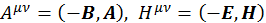(2.2.4)

Воспользуемся общим видом преобразования Лоренца для четырехмерного пространственно подобного вектора E:

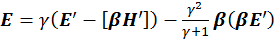(2.2.5)

В формуле (2.2.3) у нас стоит E′, поэтому нам нужно обратное преобразование формулы (2.2.5):

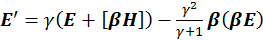(2.2.6)

Подставим полученную формулу в (2.2.3), окончательно получим:

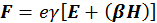(2.2.7)

По свойству всех пространственно подобных векторов, можно записать:

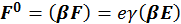(2.2.8)

Таким образом, мы нашли все компоненты вектора :

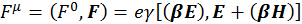(2.2.9)

Или можно воспользоваться в правой части четырехмерными обозначениями:

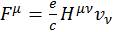(2.2.10)

Здесь — тензор внешнего электромагнитного поля.

Формула (2.2.10) и есть формула для нахождения силы Лоренца. Компоненты этого вектора можно проверить прямым вычислением, подставляя конкретные значения μ, но мы эту процедуру проделывать не будем.

§ 2.3. Вариационный принцип Гамильтона в релятивистской механике

Согласно принципу Гамильтона, вариация действия для истинного движения должна равняться нулю:

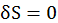(2.3.1)

Следует ввести само понятие действия. Согласно механике Ньютона, действие выглядит как

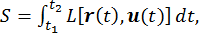(2.3.2)

где L(r,u) — функция Лагранжа, описывающая состояние частицы. Таким образом, состояние системы в любой момент времени полностью определяется начальными значениями переменных r и u. В этом смысле функция Лагранжа является функцией состояния.

В релятивистской механике такое определение для действия уже не подходит, так как оно не удовлетворяет условию инвариантности вследствие неабсолютности времени. Обобщим это действие на случай релятивистской механики:

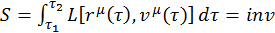(2.3.3)

Перейдем непосредственно к взятию вариации от «нового» действия. Сначала оговорим, что здесь понимается под вариацией.

В нерелятивистской механике, если заданы истинные координаты 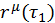и 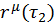, заданные таким образом, что между ними возможны различные типы движения, то через них проходит бесконечное количество виртуальных траекторий, среди которых существует только одна истинная, по которой действительно происходит движение. Вариацией 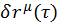на истинной траектории будет множество всех отклонений значений от истинного в данный момент времени. Взятие вариации подобно правилам дифференциала. Выполняя дифференцирование, аргументу дается приращение и дифференциал есть разность функции для начального и конечного моментов интервала . То есть, это приращение, которое получает функция при изменении аргумента на величину . Дифференциал вычисляется для бесконечно малого ненулевого отрезка времени.

Возьмем вариацию, аналогично правилам взятия дифференциала:

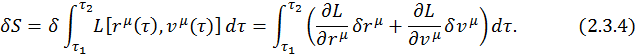
Второе слагаемое в интеграле можно проинтегрировать по частям

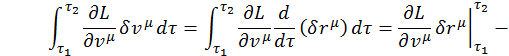
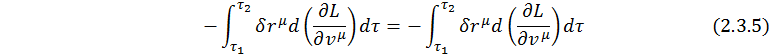
Здесь 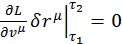, так как вариация в заданных концах траектории равняется нулю.

В таком случае выражение для вариации действия выглядит как:

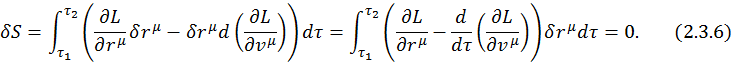
Этот интеграл всегда будет равен нулю, если в нуль обратится круглая скобка, т. к. 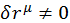— является произвольной. Следовательно:

Полученное выражение есть уравнение Эйлера-Лагранжа для релятивистской механики. Единственное отличие от нерелятивистского случая заключается в том, что здесь их не три, а четыре.

Заметим, что функция Лагранжа содержит произвол, который заключается в том, что она определяется с точностью до полной производной по времени от произвольной функции.

§ 2.4. Вывод силы Лоренца из уравнений Эйлера-Лагранжа

Чтобы получить уравнения движения, которые реализуются на практике, надо сконструировать функцию Лагранжа применительно к данной задаче. Общим требованием является то, чтобы функция Лагранжа была инвариантной величиной: