Синусоидальные электромагнитные волны
ЗАНЯТИе 1.1.4
синусоидальные электромагнитные волны
1. Обсуждение домашнего задания
1.1 Самостоятельная работа
1.1.1 Объясните, при каких условиях можно создать плоский импульс электромагнитной волны с перемещающимся участком однородных электрического и магнитного полей.
1.1.2 Как в электромагнитной волне появляется магнитное поле B?
1.1.3 Почему при распространении магнитного поля, возникает электрическое поле? Получите формулу для расчета электрического поля.
1.1.4 Почему при появлении электрического поля, возникает магнитное поле? Получите формулу для расчета модуля магнитного поля, возникшего в результате расширения области, занятой электрическим полем.
1.1.5 Проведите рассуждения, с помощью которых можно получить выражение скорости распространения электромагнитной волны.
1.1.6 Почему, однажды возникнув, электромагнитная волна может существовать самостоятельно?
Упражнения
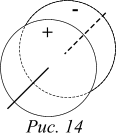 1. Покажите направления линий магнитного поля в зазоре конденсатора:
1. Покажите направления линий магнитного поля в зазоре конденсатора:
а) при зарядке конденсатора, состоящего из двух дисков;
б) при разрядке того же конденсатора.
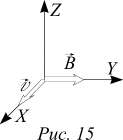
2. На рисунке 15 указаны направления вектора магнитной индукции и вектора скорости распространения электромагнитной волны (вектор скорости направлен вдоль оси OX, вектор магнитной индукции направлен вдоль оси OY). Как направлено электрическое поле?
2. Распространение синусоидальной волны
2.1 Распределение вектора E в синусоидальной волне
Рассмотренная ранее плоская электромагнитная волна обладает важным свойством — распределения электрического и магнитного полей перемещаются без изменения формы. Опыт показывает, что электромагнитная волна с любым распределением E и B обладает этим свойством.
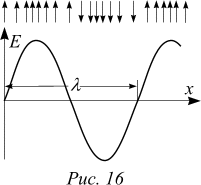
Задача 1 [C12.1.3] На рисунке изображено электрическое поле плоской синусоидальной волны в нулевой момент времени. Максимальное значение напряженности электрического поля равно E0. Положим, что скорость распространения равна v. Направление распространения вол-
ны указано стрелкой. Как зависит напряженность электрического поля от координаты x и времени.
 Решение. В решении задачи выделим три этапа:
Решение. В решении задачи выделим три этапа:
1) Математическое конструирование на основе рисунка начальной конфигурации электромагнитной волны;
2) математическое описание бегущей волны;
3) анализ уравнения бегущей волны в частных случаях (закон изменения напряженности электрического поля в данной точке, мгновенные фотографии пространственного распределения значений E.
1) Из данных о том что волна синусоидальная и из рисунка следует, что начальное распределение напряженности электрического поля описывается синусоидой с нулевой начальной фазой, т. е. E(x; t=0)=Eоsinkx, где k играет роль пространственной частоты. Поскольку l — пространственный период распределения напряженности электрического поля, постольку по аналогии с формулой, связывающей период T с частотой w=2p/T, получаем k=2p/l. Таким образом,
E(x; t=0)=Eоsin x. (1)
2) Изменение распределения напряженности с течением времени должно выглядеть как равномерный сдвиг вдоль оси OX. За время t должен накапливаться сдвиг, равный vt. Поэтому начальное распределение (1) в момент времени t превратится в
E(x; t)=Eоsin![]() (x—v t). (2)
(x—v t). (2)
Если раскроем скобки в аргументе синуса, то получим
E(x; t)=Eоsin(![]() x-2p
x-2p![]() t). (3)
t). (3)
Так как l/v =T, то, учитывая данные и соотношение w=2p/T, получаем
E(x; t)=Eоsin(kx–wt). (4)
Из проведенных выкладок очевидно соотношение v=![]() .
.
3) Отметим точку x=x1 и определим закон изменения напряженности электрического поля в этой точке. Согласно (4)
E(x1; t)=Eоsin(kx1 — wt) = — Eоsin(wt—a1 ). (5)
где a1=kx1 — начальная фаза колебаний в точке x1. Наблюдение в следующей точке x2>x1 даст колебания с той же частотой, но со сдвигом фазы a2=kx2.
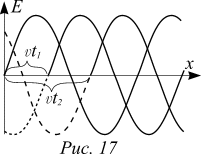
Последовательность пространственных распределений напряженности электрического поля — мгновенные фотографии распределений — изображена на рисунке 17. График распределения E(x; t1) представляет собой график E(x; 0) сдвинутый на vt1. График E(x; t2) представляет собой график
E(x; 0) сдвинутый на vt2.
 2.2 Распределение магнитной индукции в синусоидальной волне
2.2 Распределение магнитной индукции в синусоидальной волне
Рассмотрим вопрос о том, как распределено магнитное поле в электромагнитной волне. Проведем анализ, в основных чертах повторяющий анализ механизма распространения электромагнитного импульса. При этом рассмотрении новые физические идеи не возникают. Отличие имеется только в математической технике.
Задача 2. Пусть вдоль оси OX распространяется плоская синусоидальная электромагнитная волна с известным распределением электрического поля. Рассмотрим поток вектора электрического поля через узкую, шириной Dx и длины b, прямоугольную площадку перпендикулярную напряженности электрического поля, расположенную на расстоянии x от начала координат. Длинная сторона площадки параллельна фронту волны (в новой ситуации фронт — плоскость равных фаз).
а) Чему равен поток вектора напряженности электрического поля через эту площадку в момент времени t? Считайте, что на малом расстоянии Dx электрическое поле практически однородно.
б) Определите скорость изменения потока вектора напряженности электрического поля в тот же момент времени.
в) Воспользуйтесь законом полного тока и определите, чему равна разность значений магнитной индукции B(x+Dx;t)-B(x; t). При стремлении Dx к нулю отношение ![]() равно производной
равно производной ![]() в точке x в момент времени t. Попытайтесь подобрать такую зависимость B(x), чтобы производная от нее по координате x давала найденную вами в п.в зависимость. Сравните законы изменения электрического и магнитного полей. Обратите внимание на то, что взаимная ориентация вектора магнитной индукции, напряженности электрического поля и скорости распространения волны та же самая, что и в рассмотренном ранее электромагнитном импульсе.
в точке x в момент времени t. Попытайтесь подобрать такую зависимость B(x), чтобы производная от нее по координате x давала найденную вами в п.в зависимость. Сравните законы изменения электрического и магнитного полей. Обратите внимание на то, что взаимная ориентация вектора магнитной индукции, напряженности электрического поля и скорости распространения волны та же самая, что и в рассмотренном ранее электромагнитном импульсе.
Мы должны иметь в виду, что в электромагнитной волне не только магнитная индукция возникает из-за изменения электрического поля, но и в электрическое поле является следствием изменения магнитного.
Задача 3. Вернемся к физической ситуации, задачи 1. Рассмотрим магнитный поток через узкую, шириной Dx и длины b, прямоугольную площадку такую же как в задаче 2 только перпендикулярную магнитной индукции.
а) Чему равен магнитный поток через эту площадку в момент времени t? Считайте, что на малом расстоянии Dx магнитное поле практически однородно.
б) Определите скорость изменения магнитного потока в тот же момент времени.
в) Воспользуйтесь законом электромагнитной индукции и определите, чему равна разность значений напряженности электрического поя в соседних точках — E(x+Dx; t)-E(x; t). г) Имея в виду, что электрическое поле, индуцированное изменением магнитного поля, то же самое, что и поле, в результате изменения которого возникло само магнитное поле, определите скорость распространения электромагнитной волны.
В ы в о д : магнитное и электрическое поля в электромагнитной волне взаимно перпендикулярны и в заданной точке изменяются синхронно. Взаимная ориентация векторов , ![]() и
и ![]() такова, что если вектор
такова, что если вектор ![]() вращать на вектор
вращать на вектор ![]() , как рукоятку буравчика, то движение буравчика укажет направление вектора скорости. | |=с.
, как рукоятку буравчика, то движение буравчика укажет направление вектора скорости. | |=с.


