Скорость электромагнитного излучения в вакууме

2.  Скорость электромагнитного излучения в вакууме – с – является предельной скоростью передачи взаимодействия во всех ИСО.

Если рассматриваем инерциальные системы отсчета К и К´, причем К´ перемещается вдоль оси со скоростью в положительном направлении оси, то координаты точки и время событий в системах отсчета связаны преобразованиями Лоренца:

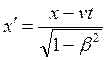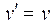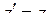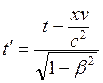; ; ; , (15.1)

где .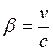

Из преобразований Лоренца следуют сокращение длины движущегося тела

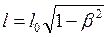, (15.2)

где – длина стержня в собственной системе отсчета; изменение темпа хода движущихся часов

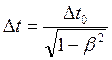, (15.3)

где – собственное время движущихся часов; правило сложения скоростей

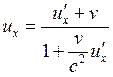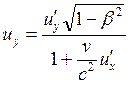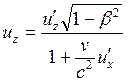, , . (15.4)

Относительно преобразований Лоренца инвариантна (то есть не изменяется при переходе между системами отсчета) величина

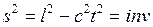, (15.5)

называемая интервалом между событиями, где – расстояние между точками, в которых произошло событие, – промежуток времени между событиями.

Вопросы для развернутых ответов

1.  Выведите из преобразований Лоренца релятивистский закон сложения скоростей и покажите, что из него следует в предельном случае классический закон сложения скоростей?

2.  Докажите инвариантность интервала

Литература: [3], глава 13,14; §62-69.

Основной блок задач

1.  С какой скоростью должно двигаться тело, чтобы его размеры сократились вдвое?

2.  Скорость тела такова, что его масса увеличилась на 20%. На сколько процентов уменьшилась длина тела в направлении движения?

3.  Во сколько раз уменьшится плотность тела при его движении со скоростью 0,8с?

4.  Релятивистская масса движущегося протона в 100 раз больше его массы покоя. Найдите его скорость.

5.  Докажите, что в релятивистском случае выполняются следующие соотношения: ; ; .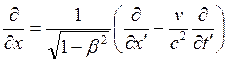

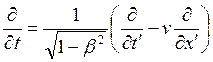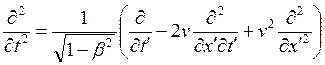Дополнительный блок задач

6.  Собственное время жизни мезона равно 2·10-6с. Как изменится его время жизни при движении со скоростью 0,99с. Какой путь он пройдет за это время?

7.  Получите формулу Физо из релятивистского закона сложения скоростей.

8.  Два пучка электронов летят навстречу друг другу со скоростями 0,9с относительно лабораторной системы координат. Какова относительная скорость электронов с точки зрения наблюдателя в лаборатории и наблюдателя, движущегося с одним из пучков.

Практическое занятие № 16

Основы релятивистской динамики

Краткие теоретические сведения

Релятивистский импульс частицы может быть записан как

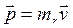, (16.1)

где 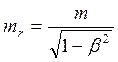(16.2) – релятивистская масса, – масса покоя частицы.

Релятивистское уравнение динамики частицы

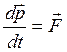, (16.3)

где – релятивистский импульс.

Полная и кинетическая энергия частицы связаны соотношением

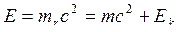, (16.4)

где – энергия покоя частицы, 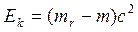– кинетическая энергия частицы.

Связь энергии и импульса записывается формулой

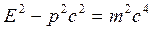, (16.5)

причем величина

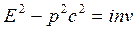(16.6)

инвариантна относительно преобразований Лоренца.

Вопросы для развернутых ответов

1.  Получите выражения для компонент релятивистского импульса и силы (по выбору отвечающего)?

2.  Докажите инвариантность величины 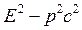относительно преобразований Лоренца.

Литература: [3], глава 15; §70-73.

Основной блок задач

1.  Плотность покоящегося тела равна . Найдите скорость системы отсчета относительно данного тела, в которой его плотность на 25% больше .

2.  Найдите скорость, при которой релятивистский импульс частицы в 1,4 раза превышает ее ньютоновский импульс.

3.  Протон движется с импульсом 10,0 Гэв/с, где с – скорость света. На сколько процентов отличается скорость этого протона от скорости света?

4.  Какую работу необходимо совершить, чтобы увеличить скорость частицы массой от 0,60с до 0,80с? Сравните полученный результат со значением, вычисленным по нерелятивистской формуле.

5.  Найдите зависимость импульса частицы массой от ее кинетической энергии. Найдите импульс протона с кинетической энергией 500 Мэв.

6.  При какой скорости кинетическая энергия частицы равна ее энергии покоя?