Сложное движение точки

Разложение векторов скорости и ускорения на составляющие, параллельные осям цилиндрической системы координат

Or, Op, Oz выразится в следующей форме:

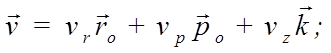
Рис. 20

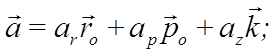
где – единичные векторы, направленные по осям цилиндриче­ской системы координат. Оси Or и Op расположены в одной плоско­сти с осями Ox и Oy.

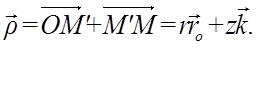Представим радиус-вектор точки М как сумму двух векторов, т. е.

Скорость точки получим дифференцированием радиус-вектора по времени:

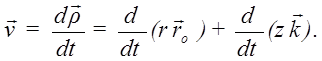
Первое слагаемое в этом выражении вычислялось при выводе ско­рости точки в полярных координатах. Во втором слагаемом постоянный по модулю и направлению единичный вектор можно вынести за знак производной. В итоге для скорости получается следующее разложение на составляющие осям цилиндрической системы координат:

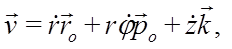
то есть, имеем, 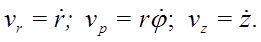так как составляющие скоро­сти, параллельные осям цилиндрической системы координат, взаимно перпендикулярны, то для модуля скорости имеем:

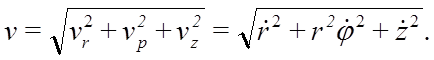
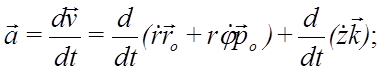Ускорение точки получим дифференцированием по времени век­тора скорости:

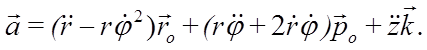
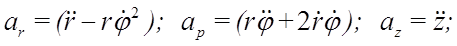Первое слагаемое в этом выражении вычислялось при выводе уско­рения в полярных координатах. Во втором слагаемом орт оси z выносим за знак производной. Получим выражение для ускорения точки в состав­ляющих, параллельных осям цилиндрической системы координат:

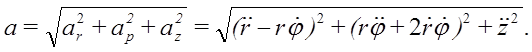
2.6. Сложное движение точки

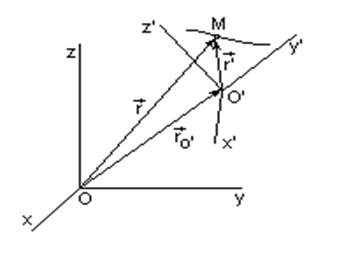
Рассмотрим движение точки М по траектории в пространстве (рис. 21). Будем рассматривать параметры ее движения из неподвиж­ной системы Oxyz и подвижной системы O’x’y’z’.

Начало отсчета О’ может двигаться посту-пательно и система O’x’y’z’ может совершать вращение относительно оси, проходящей через точку О’ с угловой скоростью и угловым ускорением . Радиус-векторы точки в системах отсчета Oxyz, O’x’y’z’, а также радиус-вектор начала отсчета О’ в си теме Oxyz связаны соотношением:

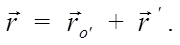
Рис. 21

Продифференцировав это соотношение по времени, получим:

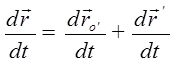
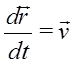
– абсолютная скорость точки (относительно системы S),

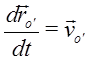
– скорость начала координат S’ относительно S,

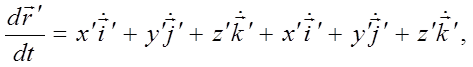не является скоростью точки М относительно системы S’, так как орты этой системы являются функциями времени.

,

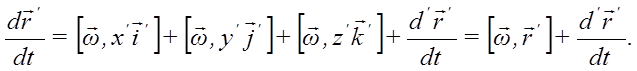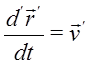Последнее слагаемое означает, что производная берется при не­изменных ортах системы O’x’y’z’: .

Теперь для скоростей имеем:

,

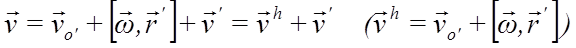
где vh–переносная, v – абсолютная, v’ – относительная скорость точки, то есть, получена связь этих скоростей.

Переносная скорость состоит из двух слагаемых: первое присут­ствует в том случае, если подвижная система отсчета движется по­ступательно, второе появляется в том случае, если подвижная система отсчета совершает вращение.

Для получения связи ускорений продифференцируем по времени соотношение для скоростей:

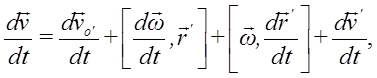
где – абсолютное ускорение, 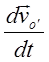– ускорение начала координат S’ относительно S.

Используем соотношение 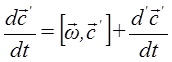, ранее полученное для и справедливое для любого вектора, разлагаемого по ортам S’, кото­рая вращается относительно неподвижной системы отсчета:

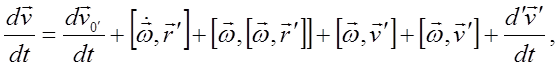
или

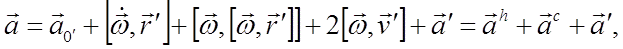
здесь переносное ускорение состоит из трех компонент.

Первая 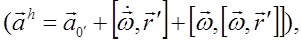присутствует, если подвижная сис­тема отсчета движется поступательно и при этом неравномерно, вто­рая появляется при неравномерном вращении подвижной системы от­счета и третья, называемая центростремительным ускорением, присутст­вует всегда, если подвижная система отсчета просто вращается.

Кориолисово ускорение 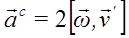присутствует у точки при двух условиях: если подвижная система отсчета вращается и точка движется относительно подвижной системы отсчета и вектор не па­раллелен вектору .

2.7. Поступательное движение твердого тела

Поступательным движением твердого тела называется та­кое его движение, при котором любая прямая, жестко связанная с телом, остается параллельной самой себе в каждый момент вре­мени.

Очевидно, достаточно, чтобы это выполнялось только для двух непараллельных прямых, связанных с телом.

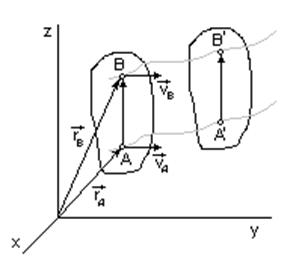Траектории точек у поступательно движущегося твердого тела могут быть не только прямыми, но и любыми кривыми, в том числе окружностями.