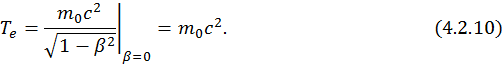Собственная масса замкнутой системы заряженных частиц и полей

Таким образом, .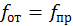

Но в действительности это квазиустойчивая система. Достаточно какому-либо заряду отклониться в сторону, как равновесие нарушится. Более строго это утверждение было сформулировано Ирншоу в виде теоремы.

Теорема Ирншоу гласит, что устойчивой системой статистически расположенных в пространстве зарядов не существует.

Докажем эту теорему.

Рассмотрим вопрос об устойчивости статической системы электрических зарядов, когда они все покоятся. Электростатическая энергия системы зарядов определяется следующим выражением:

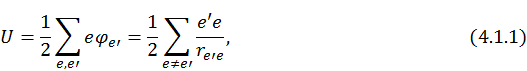
здесь 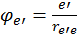– потенциал, создаваемый -зарядом в точке, где находится — заряд; а

Множитель объясняется попарным взаимодействием зарядов.

Для того чтобы система была устойчива, необходимо, чтобы энергия имела минимум, т. е. все ее первые производные по координатам должны равняться нулю. И, кроме того, все вторые производные от по координатам каждого заряда должны быть положительными.

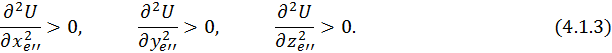
Но оказывается, что эти два условия одновременно выполнятся не могут, т. к. сумма вторых производных равна нулю:

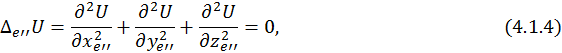
а значит, все они не могут быть одновременно положительными.

Покажем, что это равенство действительно выполняется.

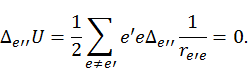
Здесь возможны два случая:

1)  когда 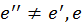, тогда все производные равны нулю;

2)  когда 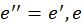, тогда

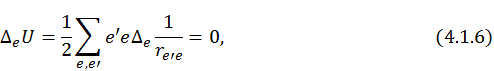
т. к. .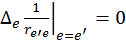

Для простоты предположим, что -заряд находится в начале координат, тогда

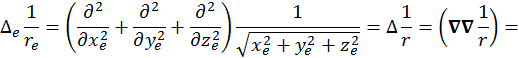
Следовательно, минимума энергии не существует, поэтому устойчивой системы нет.

Теорема Ирншоу: Невозможно создать устойчивую статическую систему разноименных зарядов. Устойчивая система возможна лишь для движущихся зарядов, из-за которых возникают механические силы, компенсирующие электрические силы.

§ 4.2. Собственная масса замкнутой системы заряженных частиц и полей

Замкнутая система заряженных частиц и полей – это такая система, которая поддерживает свое устойчивое состояние за счет внутренних сил. Согласно теореме Ирншоу, эта система должна состоять из движущихся заряженных частиц, которые взаимодействуют между собой посредством электромагнитных полей, создаваемых заряды этих частиц. Так как частицы движутся, они создают не только кулоновские электромагнитные поля, а также электромагнитные поля в виде электромагнитных волн, которые уходят на бесконечность. Причем, потери энергии (см. (3.11.7)):

Будем считать потери энергии незначительными.

Для замкнутой системы имеем закон сохранения энергии

где – сумма энергий отдельных частиц; и закон сохранения импульса

где

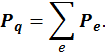
Здесь

а (см. (3.12.16))

Оба закона можно объединить в один закон сохранения энергии-импульса, если ввести четырехмерный вектор импульса замкнутой системы:

Как мы уже знаем, произведение четырехмерных векторов образует инвариант

Определим собственную массу замкнутой системы согласно соотношению

а с другой стороны с учетом (4.2.2)-(4.4.4)

Приравнивая (4.2.5) и (4.2.6) получим выражение для собственной массы замкнутой системы:

Т. к. эта величина является инвариантом, то проще всего ее вычислять в системе покоя. Для простоты рассмотрим систему, состоящую из одного заряда и кулоновского поля, которое он создает. Тогда для покоящегося электрона получим, что импульс

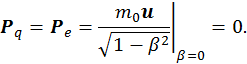
Полевой импульс также равен нулю, т. к. магнитное поле покоившегося заряда отсутствует:

Тогда для собственной массы системы получим

где энергия частицы