Сокращение продольных размеров движущихся тел

4.  Сокращение продольных размеров движущихся тел

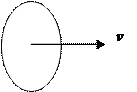
Рассмотрим мяч, который движется со скоростью порядка скорости света. Для стороннего наблюдателя этот мяч будет выглядеть как диск (рис. 12).

Рис.12
Штрихованная система	Система отсчета, связанная с наблюдателем

Как возникает это явление?

В штрихованной системе расположим линейку, ее длина .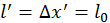

Какова длина линейки в лабораторной системе? Запишем преобразования Лоренца для приращений координат и времени:

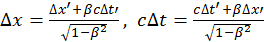(1.5.8)

При выводе делается предположение, что оба конца линейки измеряются в один момент лабораторного времени, т. е. 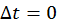. Следовательно, 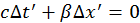или .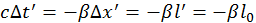

Здесь -длина самой линейки в покоящейся системе.

Подставим:

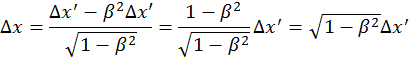
Таким образом, линейные размеры движущегося тела для стороннего неподвижного наблюдателя уменьшаются в направлении движения при скоростях движения близких к скорости света.

Отсюда вытекают несколько следствий:

1)  Если сокращаются только продольные размеры, то будет изменяться объем самого тела.

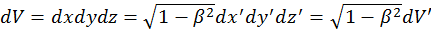(1.5.9)

2)  Элементарный объем четырехмерного пространства остается без изменения

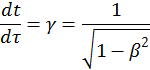
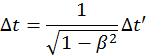
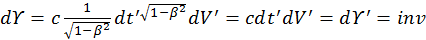(1.5.10)

§ 1.6. Ковариантная форма преобразований Лоренца

Ранее были получены преобразования Лоренца для координат и времени:

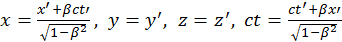(1.6.1)

Эти формулы не являются ковариантными. Здесь выделены отдельные координаты и время, тогда как ковариантные формы подразумевают отсутствие выделенных координат.

Преобразование Лоренца для координат в ковариантной форме имеет вид:

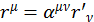(1.6.2)

— матрица, которая представляет собой коэффициенты преобразования. Эти коэффициенты постоянны.

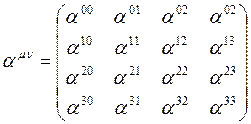
Нам осталось найти коэффициенты α, µ и ν. Сравним уже известные нам преобразования Лоренца для координат и времени с ковариантной формой.

Положим µ=0:

Сравнивая, получаем:

Аналогично получим для µ=1:

Откуда находим

Таким образом, матрица преобразования Лоренца для случая, когда система движется вдоль оси «неподвижной» системы имеет следующий вид:

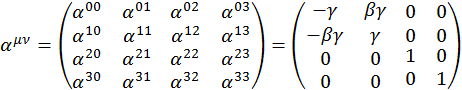(1.6.3)

Если речь идет об обратном преобразовании Лоренца, то вместо матрицы следует использовать обратную матрицу :

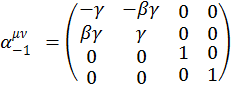(1.6.4)

Очевидно, что 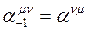, то есть :

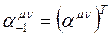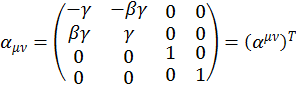(1.6.5)

Иначе, матрица удовлетворяет следующему условию:

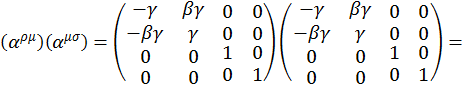
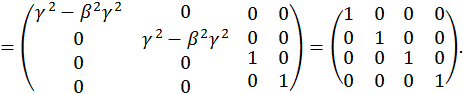(1.6.6)

Нам надо убедиться в правдивости найденных коэффициентов. Для этого должно выполняться :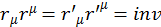

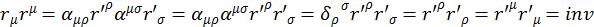, ч. т. д. (1.6.7)

В частном случае может случиться, что L=0. Следовательно,

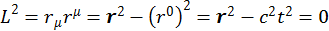. (1.6.8)

С математической точки зрения это есть уравнение конуса в четырехмерном пространстве, вершина которого лежит в начале координат. Рассмотрим сечение 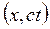четырехмерного пространства. Вспомним, что 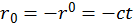и 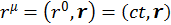.