Теорема остроградского-гаусса
– поток через замкнутую поверхность.
3.2. Теорема Остроградского-Гаусса
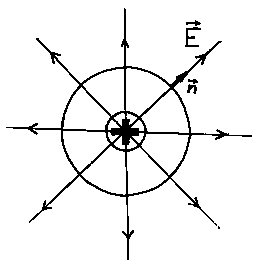
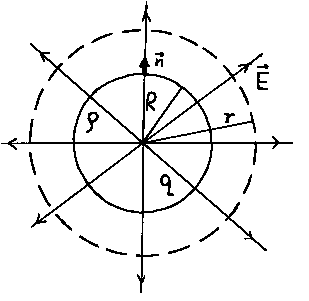
Пусть имеется уединенный точечный заряд. Рассчитаем поток вектора этого заряда через замкнутую поверхность, окружающую этот заряд.
1. Сфера.
|
Рис. 3.5. |
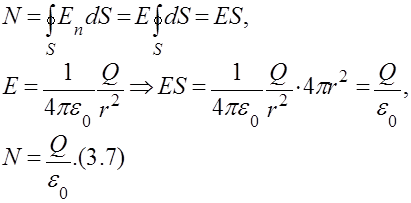
Поток вектора напряженности равен величине заряда, деленной на ![]() .
.
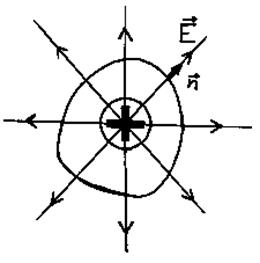
Окружим заряд замкнутой поверхностью произвольной формы. Возможно два случая: выпуклая поверхность и поверхность с “морщинами”.
|
Рис. 3.6. |
В случае с выпуклой поверхностью результат такой же, как и для сферической, а во втором случае можно показать, что суммарный поток, создаваемый при пересечении линиями напряженности “морщин”, будет равен 0, т. к. при расчете скалярного произведения косинус угла между векторами ![]() один раз будет положительным, а в другой – отрицательным (знаки косинусов указаны на рис. 3.7).
один раз будет положительным, а в другой – отрицательным (знаки косинусов указаны на рис. 3.7).
Рис. 3.7.
Поэтому можно сказать, что поток вектора напряженности поля точечного заряда через произвольную замкнутую поверхность, окружающую этот заряд, равен величине этого заряда, деленной на ![]() .
.
Пусть имеется система k точечных уединенных зарядов 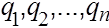 . Воспользуемся принципом суперпозиции:
. Воспользуемся принципом суперпозиции:
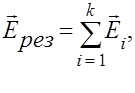
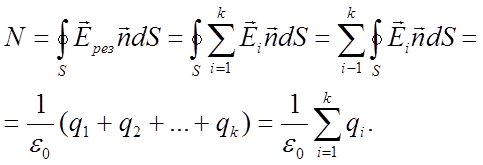 (3.8)
(3.8)
Поток вектора напряженности системы k точечных неподвижных зарядов в вакууме равен алгебраической сумме этих зарядов, деленной на ![]() .
.
В случаях, если имеется непрерывное распределение зарядов в некоторых телах, необходимо от операции суммирования перейти к операции интегрирования. Тогда получим:

![]()
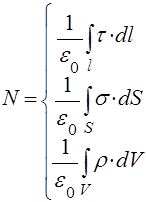
Теорема Остроградского-Гаусса в интегральной форме:
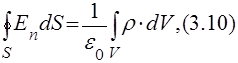
если ![]() , то зарядов нет и
, то зарядов нет и ![]()
3.3. Применение теоремы Остроградского – Гаусса
3.3.1. Поле заряженной плоскости.
1. Линии напряженности перпендикулярны плоскости.
2. Их густота одинакова.
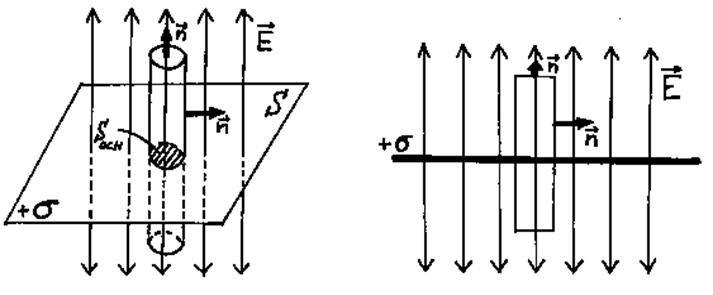
Рис. 3.8.
Так как плоскость бесконечна, то исходя из соображений симметрии значение модуля ![]() в каждой точке одинаково.
в каждой точке одинаково.
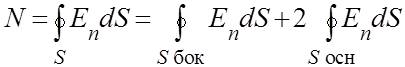 ,
,
т. к. проекция вектора на нормаль к боковой поверхности равна нулю, то
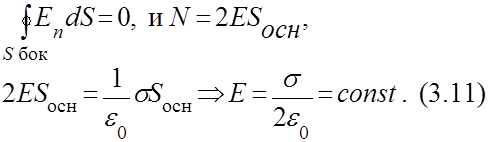
3.3.2. Поле разноименных плоскостей
Применим принцип суперпозиции (рис.3.9):
1.Напряжённость поля в области пространства между заряженными плоскостями будет равна:
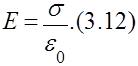
2.Напряжённость поля вне заряженных плоскостей равна 0.Это означает, что электрическое поле сосредоточено в пространстве между заряженными плоскостями.
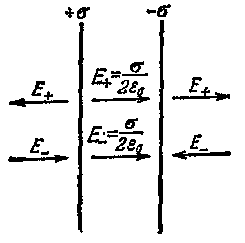
Рис. 3.9. Рис. 3.10.
На рисунке 3.10 показаны силовые линии электрического поля двух разноименно заряженных плоскостей.
3.3.3. Поле заряженной нити (рис.3.11)
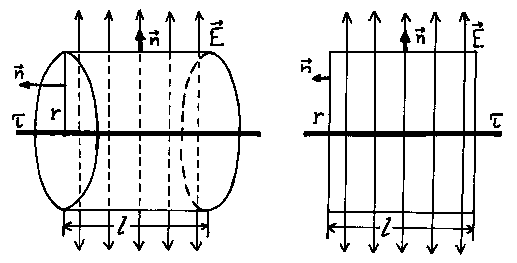
Рис. 3.11.
|
Рис. 3.12. |
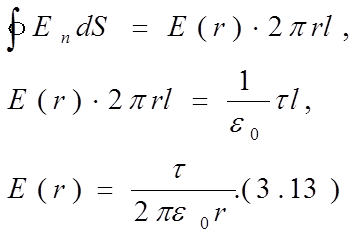
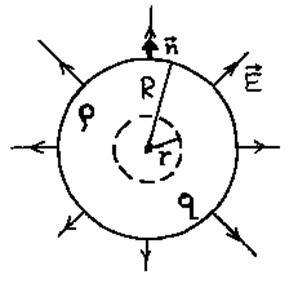
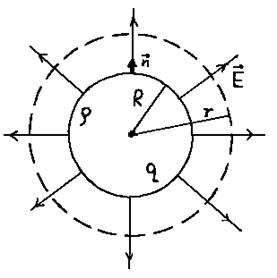
3.3.4. Поле заряженной сферы.
Поле внутри сферы: (рис. 3.12)
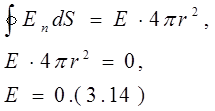
Поле вне сферы (рис. 3.13)
|
Рис. 3.13. |
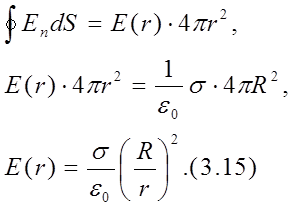
Т. к. 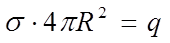 , то
, то
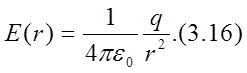
Если 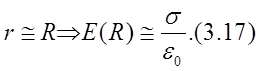
3.3.5. Поле заряженного шара.
Поле внутри шара (рис. 3.14)
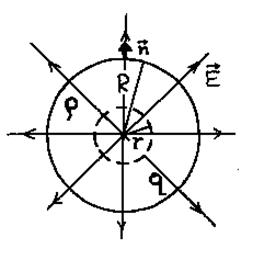
Рис. 3.14.
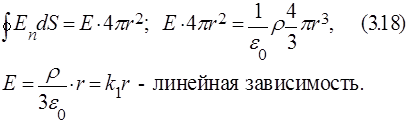
|
Рис. 3.15. |
Поле вне шара (рис. 3.15)
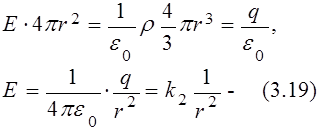
обратно квадратичная зависимость.
3.4. Аналогия и различия между электростатическим и гравитационным полями
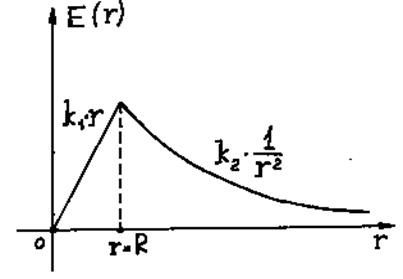
Рис. 3.16.
На рисунке 3.16 изображен график зависимости напряженности электростатического поля от расстояния.
Аналогично выглядит график зависимости ускорения свободного падения от расстояния (рис. 3.17, 3.18)