Способы нахождения мгновенного центра ускорений

Рис. 31

Мгновенный центр ускорений лежит на прямой, проведенной под углом α ( tgα=ε/ω2) к ускорению точки О.

При этом α надо отложить от ускоре­ния aO в направлении дуговой стрелки углового ускорения ε.

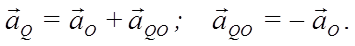Только в точках этой прямой ускорение aO и ускорение от враще­ния aQO могут иметь противоположные направления и одинако­вые по модулю значения:

Но 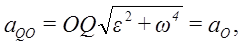следовательно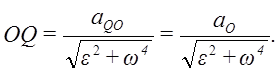

Мгновенный центр ускорений является единственной точкой фи­гуры, ускорение которой в рассматриваемый момент времени равно нулю. В другой момент времени мгновенный центр ускорений находится в общем случае в другой точке плоской фигуры.

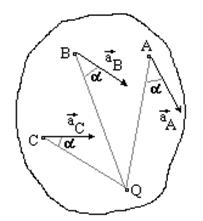
Если положение мгновенного центра ускорений известно, то вы­брав его за полюс, для ускорения произвольной точки А, имеем:

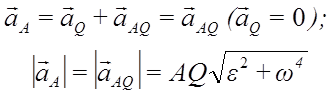
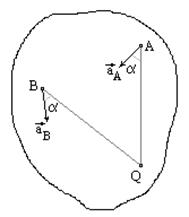и ускорение aA направлено под углом α к отрезку AQ, соединяющего точки A и Q в сторону дуговой стрелки ε (рис. 32).

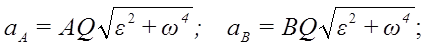Ускорения двух точек A и B показаны на рисунке, их величины равны

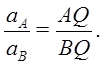
Рис. 32

Следовательно, ускорения точек плоской фигуры при плоском движении можно определить так же, как и при вращательном движе­нии плоской фигуры вокруг мгновенного центра ускорений с угловой скоростью ω и угловым ускорением ε.

Для вычисления скоростей принимают, что фигура вращается во­круг мгновенного центра скоростей, для вычисления ускорений принимают, что фигура вращается вокруг мгновенного центра уско­рений. В общем случае эти центры являются разными точками пло­ской фигуры.

Ускорения точек плоской фигуры при плоском движении подобно скоростям точек можно вычислить двумя способами: по формуле 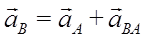, выражающей зависимость ускорений двух точек пло­ской фигуры (способ 1) и по формуле 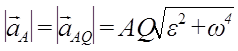, используя мгновенный центр ускорений (способ 2). Часто мгновен­ный центр ускорений (кроме случаев, когда ω или ε равных нулю) располагается так, что трудно определить расстояние от него до рас­сматриваемых точек фигуры, поэтому рекомендуется использовать способ 1 через формулу, связывающую ускорения точек фигуры.

Способы нахождения мгновенного центра ус­корений.

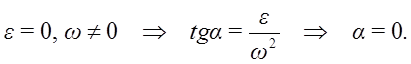
1.

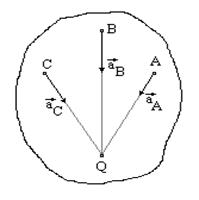
Ускорения всех точек направлены к мгновенному центру ускорений (Рис. 33), так как они состоят только из одной нормальной составляющей от вращения вокруг мгновенного центра ус

Рис. 33 корений.

Если известно aA, то AQ = aA/ω2.

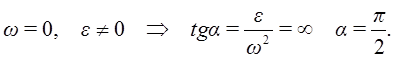
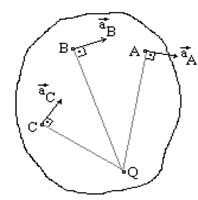
2.

мгновенное поступательное движение (Рис. 34). Мгновенный центр ускорений лежит на пересече­нии перпендикуляров к ускорениям точек.

Рис. 34

Если из­вестно aA, то AQ = aA/ε.

3.

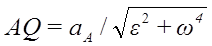Имеем общий случай, ранее уже обсуждавшийся. Угол α откладываем по дуговой стрелке ε от век­тора ускорения (Рис. 35).

Если известно aA, то

Рис. 35

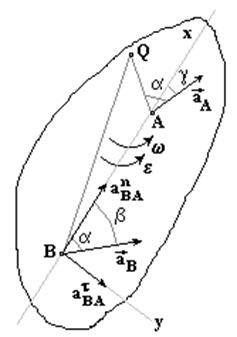4. Пусть в данный момент времени известны ускорения двух точек плоской фигуры A и B (Рис. 36). Приняв за полюс точку A, имеем:

(*),

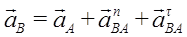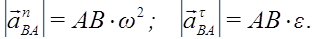где

Проецируя левую и правую части вектор­ной формулы (*) на оси Bx и By получаем:

,

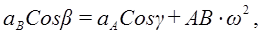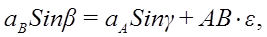
Рис. 36

где β и γ в принципе известные углы.

Проекцию anBA на ось Вх берем со знаком (+), так как она всегда на­правлена к оси вращения (к полюсу). Проекцию aτBA, берем со знаком (+) предполагая, что стрелка ε направлена против часовой стрелки.

Из уравнений проекций находим

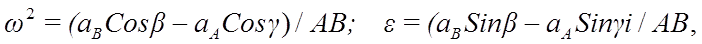
знак ε определяется после подстановки данных в формулу.

После того, как найдены ε и ω, задача нахождения мгновенного центра ускорений сводится к случаю 3.

Вопросы для самопроверки:

1. Как задается скорость и ускорение в декартовой системе координат?

2. Какие системы координат Вы знаете?

3. Какое движение называется абсолютным, относительным, переносным?

4. Какое движение называется поступательным?

5. Какое движение называется вращательным?

6. Как определить мгновенный центр скоростей?

7. Как определить мгновенный центр ускорений?

3. ДИНАМИКА

3.1. Основные понятия

Динамикой называется раздел механики, в котором изучается движение материальных тел под действием сил.

В динамике, в отличие от кинетики, при изучении движения тел принимают во внимание как действующие на них силы, так и инертность самих материальных тел.

Инертность тела проявляется в том, что оно сохраняет свое дви­жение при отсутствии действующих сил, а когда на него начинает действовать сила, то скорость точек тела изменяются не мгновенно, а постепенно и тем медленнее, чем больше инертность этого тела. Ко­личественной мерой инертности материального тела является физи­ческая величина, называемая массой тела. В классической механике масса m рассматривается как величина скалярная, положительная и постоянная для каждого данного тела.

Кроме суммарной массы движение тела зависит еще в общем случае от формы тела, точнее от взаимного расположения образую­щих его частиц, т. е. от распределения масс в теле.

Чтобы при первоначальном изучении динамики отвлечься от учета тела (распределения масс), вводят абстрактное понятие о мате­риальной точке, как о точке, обладающей массой, и начинают изуче­ние динамики с динамики материальной точки.

3.2. Классификация сил. Динамика материальной точки

Сила тяжести – постоянная сила, действующая на тело, находя­щееся вблизи земной поверхности. P= mg,

где m – масса тела, g – ускорение свободного падения.

Сила упругости – P = cλ,

где c – коэффициент жесткости, λ – перемещение тела.

Сила трения – P = fN,

где f – коэффициент трения, N – нормальная реакция.

Сила тяготения – сила с которой притягиваются к друг к другу два материальных тела P = fm1m2/r2,

где f – гравитационная постоянная, m1 и m2 – массы двух тел, r – рас­стояние между центрами этих тел.

Сила вязкого сопротивления – P = μv ,

где μ – коэффициент сопротивления среды, v – скорость тела.

Движение материальных точек и тел следует рассматривать от­носительно определённой системы отсчёта. В классической механике в основу, которой положены законы И. Ньютона, такая система на­зывается инерционной системой отсчёта. Пространство считается трёхмерным эвклидовым пространством, свойства которого не зави­сят от движущихся в нём материальных объектов.