Тензор напряжений

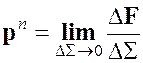. (2.5)

Определенная таким образом характеристика называется вектором напряжений в точке , на площадке с нормалью . Если теперь рассмотрим воздействие частиц, находящихся в , на частицы, находящиеся в , то совершенно аналогично обнаружим, что это воздействие сводится к результирующей силе и результирующему моменту . Но и внешняя нормаль на этой площадке . Тогда вектор напряжений на этой площадке можно определить как

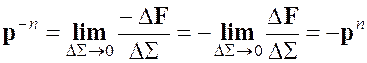. (2.6)

Таким образом, при смене направления нормали на противоположное, вектор напряжений меняет знак на противоположный.

2.7 ТЕНЗОР НАПРЯЖЕНИЙ

Введенный вектор напряжений характеризует внутреннее состояние силовых взаимодействий частиц друг на друга. Эта характеристика обладает свойством зависимости от расположения элементарной площадки, или направления вектора . Выведем правило нахождения вектора напряжений на любой площадке через напряжения на трех координатных поверхностях. Для этого воспользуемся декартовой прямоугольной системой координат и рассмотрим элементарный триэдр, вырезанный в некоторой точке СС см. рис. 5. Пусть на него действует массовая сила . Кроме того, тетраэдр находится внутри сплошной среды, поэтому воздействие частиц вне тетраэдра на частицы, лежащие внутри его можно оценить как воздействие через соответствующие грани в виде векторов напряжений . Обозначим площадь грани через . И пусть на этой грани вектор нормали . Тогда площади остальных граней могут быть выражены через компоненты вектора нормали и площадь :

.

Применяя принцип затвердевания и принцип Даламбера, запишем условие динамического «равновесия» тетраэдра

,

где — высота тетраэдра, проведенная из точки , — ускорение тетраэдра. Воспользуемся основным свойством вектора напряжений (2.6), разделим обе части равенства на и перейдем к пределу, при . Сохраним в предельном переходе направление нормали , в результате получим

. (2.7)

Получили выражение вектора нормали на любой площадке, определяемой нормалью , через векторы напряжений на координатных площадках и компоненты вектора нормали.

Разложим каждый из векторов напряжений координатных площадок

(2.8)

что можно записать в виде компактной записи с учетом правила суммирования по повторяющимся индексам

Далее определим компоненты вектора нормали

.

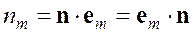Тогда соотношение (1.28) можно переписать в виде

.

В этом равенстве введен новый объект – тензор напряжений, через который определяется вектор напряжений на площадке с нормалью . В дальнейшем часто будет применяться полученная только что формула

. (2.9)

Формулы (1.30) дают возможность изучать компоненты тензора напряжений. Действительно, на рис. 6. изображен элементарный куб, на гранях которого действуют соответствующие компоненты тензора напряжений.

На этом рисунке изображены только грани, которые имеют нормали, совпадающие с направлением координатных базисных векторов. На противоположных гранях нормали направлены в противоположные стороны, и согласно (1.28) компоненты тензора напряжений имеют противоположные направления.

2.8 ГЛАВНЫЕ НАПРАВЛЕНИЯ И ГЛАВНЫЕ НАПРЯЖЕНИЯ

По аналогии с тензором деформаций можно отметить, что тензор напряжений второго ранга имеет три инварианта, не зависящие от ориентации системы координат (дальнейшие формулы приведем в декартовой прямоугольной системе координат):

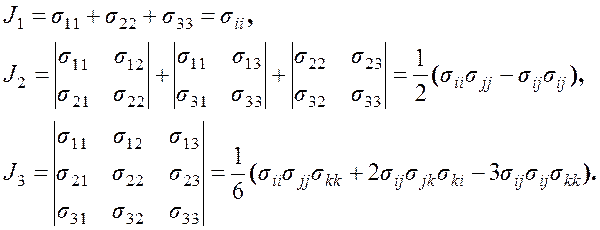(2.10)

Для тензора напряжений также интересна задача определения для данной точки области тех направлений, в которых вектор напряжения коллинеарен выбранному направлению. Если преобразовать компоненты тензора напряжений к таким осям, то для этих направлений тензор напряжений будет шаровым. Отсюда получаем, что если такие направления существуют, то должны выполняться условия коллинеарности векторов и , т. е. должны выполняться равенства ( — коэффициент пропорциональности)

.

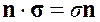В силу симметрии тензора напряжений предыдущее равенство можно переписать в компонентах декартовой системы координат

.

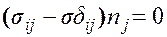Условия разрешимости этих уравнений приводят к характеристическому уравнению для тензора напряжений