Тензор плотности энергии-импульса электромагнитного поля

§ 3.10. Тензор плотности энергии-импульса электромагнитного поля

В качестве исходного соотношения воспользуемся второй парой уравнений Максвелла:

Кроме того, будем использовать четырехмерный вектор плотности силы:

Возьмем из и подставим в .

Рассмотрим второй член выражения (3.9.3) более подробно:

Используя первую пару уравнений Максвелла, перепишем (3.9.4) следующим образом:

С учетом (3.9.5) выражение (3.9.3) запишется так:

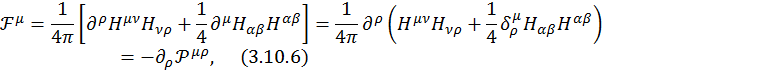
где — тензор плотности электромагнитного поля.

Выражение (3.9.7) – окончательное выражение для тензора плотности электромагнитного поля. Теперь найдем его компоненты. Учитывая, что этот тензор симметричный, при µ=0 получаем

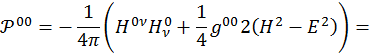
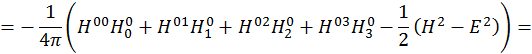
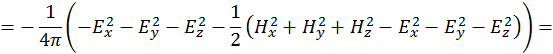
где – плотность энергии электромагнитного поля.

В качестве упражнения предлагается вычислить компоненты тензора второго ранга. Мы воспользуемся ответом к этой задаче:

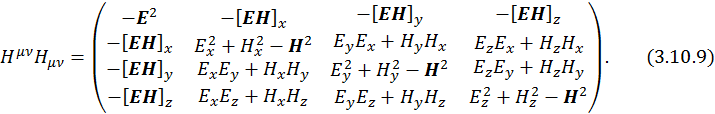
Тогда, зная компоненты (3.10.9), можно вычислить или .

так как 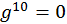и, следовательно,

Здесь – вектор Пойнтинга или Умова – Пойнтинга, это поток энергии электромагнитного поля, т. е. количество энергии, которое проходит в единицу времени через единицу площади, нормально к ней.

Тензор напряженностей Максвелла имеет вид:

где i,j принимают значения 1, 2, 3.

Таким образом, получаем

§ 3.11. Вектор Пойнтинга и мощность электромагнитного излучения

Рассмотрим физический смысл отдельных компонент тензоров плотностей энергии импульса.

где – плотность энергии поля, – плотность кинетической энергии частиц.

Найдем выражение для .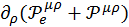

При 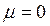получаем:

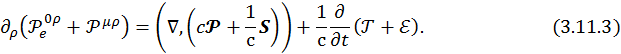
Умножим обе части (3.11.3) слева на dV и проинтегрируем по всему объему^

где – энергия поля, которая находится внутри рассматриваемой поверхности. Если от объемного интеграла с div перейдем к поверхностному интегралу, мы можем устремить ее на бесконечность, а заряд находится внутри, следовательно, за счет -функции первый член

Остается

Здесь вектор направлен наружу от замкнутой поверхности, по которой идет интегрирование.

Это выражение (3.11.6) означает, что изменение полной энергии внутри замкнутой поверхности равно количеству энергии, которое вытекает через поверхность наружу (при условии, что система теряет энергию). Таким образом, мы получили энергетический баланс.

Если речь идет о мощности (энергия, теряемая системой в единицу времени) излучения, то она равна

Из этого следует, что вектор Пойнтинга представляет собой количество энергии электромагнитного поля, которое проходит в единицу времени через единицу площади, нормально к ней. Это соотношение (3.11.7) получено из закона сохранения энергии-импульса (3.11.6).

§ 3.12. Тензор натяжения Максвелла и пондеромоторные силы

Как мы уже знаем
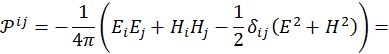