Теорема об изменении кинетической энергии точки

и третье слагаемое в предыдущей формуле обращается в ноль (выра­жение в круглых скобках в системе отсчета, связанной с центром масс, равно нулю).

В итоге получаем:

Это означает, что кинетическая энергия системы в абсолютном движении складывается из кинетической энергии центра масс, как если бы в нем была сосредоточена вся масса системы, и кинетической энергии системы относительно центра масс.

Примеры:

1. Кинетическая энергия твердого тела при поступательном движении –

2. Кинетическая энергия твердого тела при вращении вокруг не­подвижной оси:

3. Кинетическая энергия твердого тела при плоском движении:

Теорема об изменении кинетической энергии точки

Умножим скалярно обе части второго закона Ньютона на dr

После несложных преобразований получим:

или

− мощность, подводимая к этой точке.

Интегрируя

то есть изменение кинетической энергии точки на каком-либо пере­мещении равно работе силы, действующей на точку на том же пере­мещении.

Теорема об изменении кинетической энергии системы точек

Для каждой точки системы имеем:

Здесь выразили равнодействующую силу для точки mk в виде суммы равнодействующих внешних F(e) и внутренних сил F(i), дейст­вующих на точку.

Проводя суммирование и вынося знак дифференциала за знак суммы, будем иметь:

или

Получили закон изменения кинетической энергии для системы точек: «Изменение кинетической энергии системы точек равно работе все внутренних и внешних сил на всех перемещениях всех точек». Работа внутренних сил не равна нулю, поскольку под действием одинаковых сил действия и противодействия точки разной массы имеют различные перемещения, и работа внутренних сил полностью не компенсируется.

Проведя интегрирование между начальным и конечным положением системы, будем иметь:

или

Для абсолютно твердого тела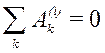 и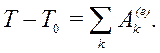

Имеем теорему в конечной форме: «изменение кинетической энергии системы при ее перемещении из одного положения в другое равно сумме работ всех внешних и внутренних сил, действующих на систему, на соответствующих перемещениях точек при том же изменении положения системы».

3.9. Потенциальное силовое поле и потенциальная энергия

Силовым полем называют часть пространства, в каждой точке которого на материальную точку действует определенная сила, зависящая от координат точки и времени (стационарный и нестационарный случаи).

Силовое поле называют потенциальным, если имеется силовая функция , такая, что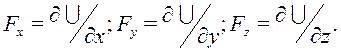

Силовая функция определяется с точностью до постоянной, так как добавка в виде константы под знак частной производной не влияет на значения Fx, Fy, Fz.

Запишем работу силы потенциального силового поля:

Элементарная работа силы в потенциальном силовом поле равна полному дифференциалу от силовой функции.

Полная работа силы на участке от положения М0 до положения М равна

Эта работа не зависит от формы траектории, работа силы в потенциальном силовом поле по замкнутой траектории равна нулю.

Можно показать, что необходимым и достаточным условием того, что силовое поле является потенциальным, является условие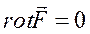, то есть поле безвихревое.

Непотенциальными являются силы сопротивления, зависящие от скорости и силы трения. Сила сухого трения скольжения не будет потенциальной, так как хотя она постоянна и не зависит от скорости, но направление силы трения от скорости зависит.

Наряду с силовой функцией можно ввести другую функцию, характеризующую запас энергии в данной точке поля – потенциальную энергию.

Потенциальной энергией П материальной точки в рассматриваемой точке силового поля M называют работу, которую совершают силы поля, действующие на материальную точку при перемещении ее из положения M в начальное положение M0:

Постоянная С0 одна и та же для всех точек поля, зависящая от того, какая точка поля была выбрана за начало отсчета.

В конечном итоге имеем: то есть силовая функция и потенциальная энергия отличаются знаком о определены с точностью до постоянной.

3.10. Закон сохранения механической энергии

Для материальной точки ранее имели: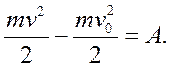

Если материальная точка движется в стационарном потенциальном силовом поле, то А = П0 − П, то есть

При движении точки в стационарном потенциальном силовом поле ее полная механическая энергия, равна сумме кинетической и потенциальной энергии, остается постоянной величиной. Это и является формулировкой закона сохранения полной механической энергии.

Для системы точек энергии в стационарном потенциальном силовом поле

где П − потенциальная энергия внутренних и внешних сил, действующих на точки системы. Отсюда

Т − Т0 = П0 − П или Т + П = Т0 + П0 = Е = Е0,

то есть полная механическая энергия при движении системы в стационарном силовом поле внешних и внутренних сил является постоянной величиной.

Для твердого тела П − потенциальная энергия внешних сил, так как потенциальная энергия внутренних сил постоянна и может быть положена равной нулю. Для изменяемой механической системы учитываем потенциальную энергию и внутренних сил.

Если для системы выполняется закон сохранения механической энергии, то она называется консервативной.

Диссипативные силы характерны тем, что приводят к уменьшению механической энергии Е (переводя ее в тепло).

Вопросы для самопроверки:

1.  Дайте определение динамики.

2.  Дайте определение следующих сил: тяжести, упругости, трения, тяготения, вязкого сопротивления

3.  Дайте определение 1, 2, 3 законов Ньютона.

4.  Как определяется уравнение движения материальной точки?

5.  Дайте определение внешних и внутренних сил материальной системы.

6.  Как определяется момент инерции?