Теория моментов сил

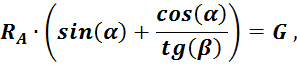
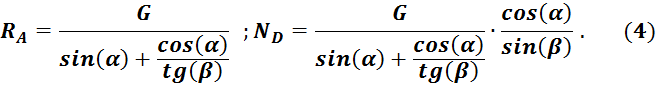
7. ТЕОРИЯ МОМЕНТОВ СИЛ

7.1. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ЦЕНТРА

Вектор 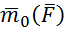перпендикулярен плоскости 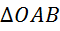; направлен в ту сторону, откуда поворот виден против часовой стрелки (рис. 17а); определяется векторным произведением

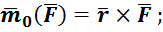
модуль вектора

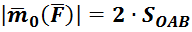
– это площадь параллелограмма со сторонами и (рис. 17б).

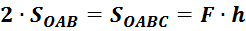
Свойства момента силы:

1) не изменяется при переносе силы по линии её действия;

2) равен нолю, когда 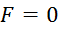или .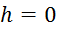

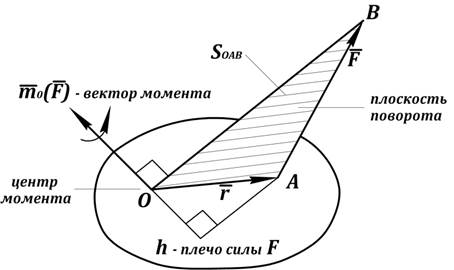
а)

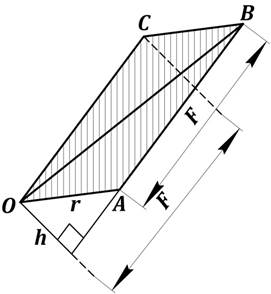
б)

Рис. 17. Момент силы относительно центра

7.2. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ОСИ

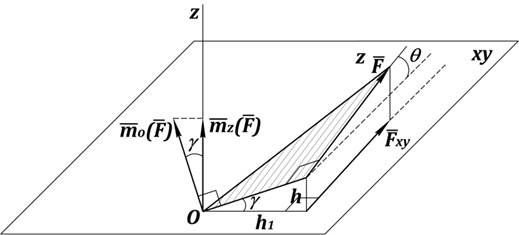
Рис. 18. Момент силы относительно оси

и – в пространстве;

и – в плоскости (рис. 18);

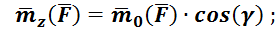
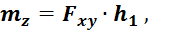
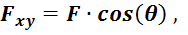
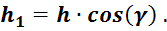
7.3. АНАЛИТИЧЕСКИЕ ФОРМУЛЫ ДЛЯ МОМЕНТОВ ОТ ПРОЕКЦИЙ СИЛЫ ОТНОСИТЕЛЬНО КООРДИНАТНЫХ ОСЕЙ

Даны координаты 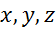точки приложения силы и проекций 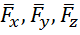(рис. 19).

Проекция момента силы на ось , как сумма моментов от проекций :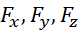

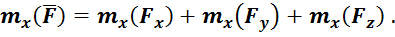
Так как параллельна , то

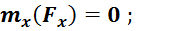
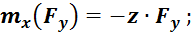
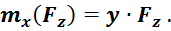
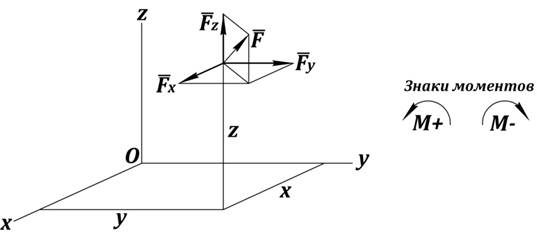
Рис. 19. Момент от проекций силы относительно координатных осей

По мнемоническому (от греч. мнемоника (mnemo – память; Мнемозина – богиня памяти) – искусство запоминания путём образования ассоциаций) правилу круговой перестановки индексов и координат против часовой стрелки (рис. 20) получаем

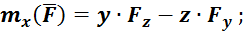
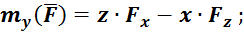
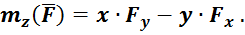
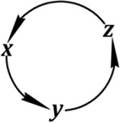
Рис. 20. Правило круговой перестановки индексов и координат

8. ТЕОРИЯ ПАР СИЛ

8.1. ОСНОВНЫЕ ПОНЯТИЯ

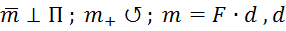– плечо пары сил (рис. 21).

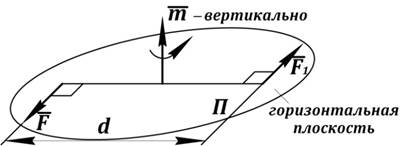
Рис. 21. Пара сил

8.2. ТЕОРЕМА ОБ ЭКВИВАЛЕНТНОСТИ ПАР СИЛ

Формулировка: две пары сил, имеющие одинаковые моменты, эквивалентны.

Доказательство:

В плоскости П дана пара сил и с плечом (рис. 22а).

Выполняется разложение каждой силы на 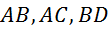(рис. 22б).

Пара , на плече заменилась на пару , на плече (рис. 22в).