Теория пар сил
![]()
![]()
Могут использоваться 2 или 3 уравнения моментов.
 Пример
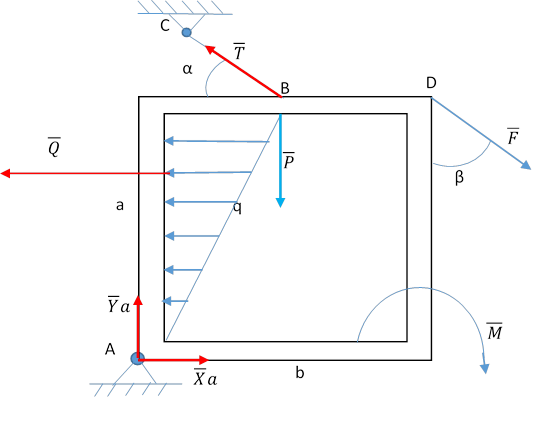
Пример
Составим уравнение суммы всех сил на ось X и Y:
![]()
![]()
Сумма моментов всех сил относительно точки А:
![]()
Параллельные силы
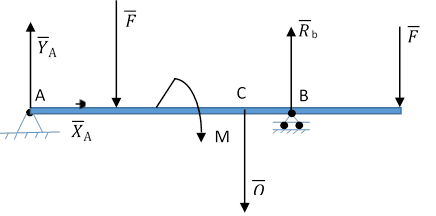 |
Уравнение относительно точки А:
![]()
![]()
Уравнение относительно точки В:
![]()
![]()
Сумма проекций сил на ось У:
![]()
![]()
Теория пар сил
Система двух равных по модулю параллельных противоположно направленных сил, называется парой сил.
Пара не имеет равнодействующую, её можно уравновесить только другой парой и можно представить в виде вектор-момента.
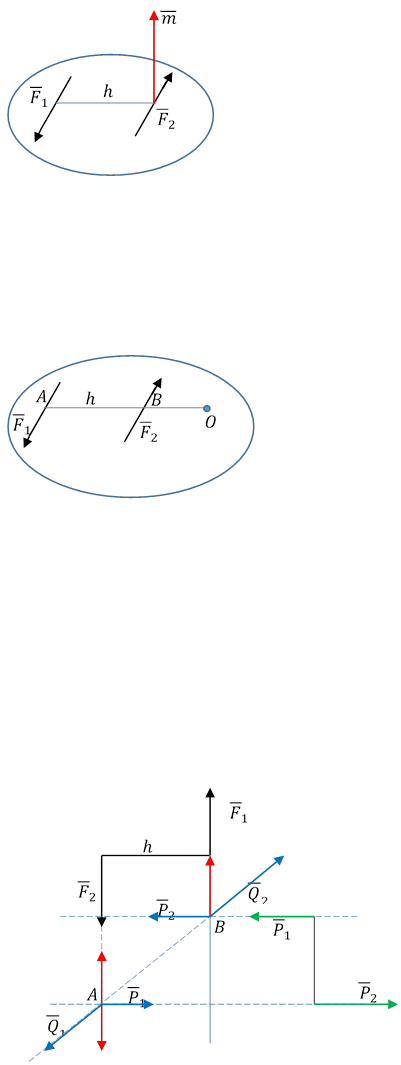 |
![]()
Свойства пар сил
1) Пару сил можно переносить в плоскости её действия произвольно, не изменяя её действие.
2) Момент пары не зависит от выбора центра.
Покажем, что сумма моментов сил относительно любого центра не зависит от выбора центра и равняется сумме момента.
![]()
Теорема об эквивалентности. Сложение пар сил в пространстве
Две пары, имеющие равные моменты – эквивалентны.
Продолжим векторы и отметим точки A и B.
![]()
![]()
![]()
Следовательно, две пары, имеющие равные моменты эквивалентны.
Можно произвольно менять модули сил и плечо пар, сохраняя неизменными их момент.
Перенос пары в параллельную плоскость
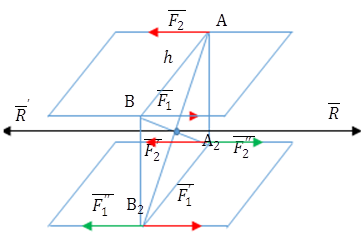 |
Плоскости I и II должны быть параллельны, в частности, они могут совпадать.
Если приложить ![]() и
и ![]() и совместить точки приложения сил с проекциями точек, то получим:
и совместить точки приложения сил с проекциями точек, то получим:
![]()
![]()
Силы равны по модулю, поэтому их равнодействующие R и R’ должны быть приложены в точке пересечения диагоналей прямоугольника ABB1A1, кроме того, они равны по модулю и направлены в противоположные стороны. Это означает, что они составляют систему, эквивалентную нулю.
Таким образом:
1) Пару сил можно переносить в параллельную плоскость. Произвольно менять модули сил и плечо, сохраняя момент. Две пары можно привести к одному плечу.
2) Пару сил можно перемещать в плоскости её действия.
Вектор – момент пары можно считать свободным вектором.
Если не плечо действует система пар сил, то складывая их геометрически получим главный вектор – момент равнодействующей пары, равный сумме векторов.
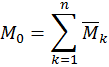
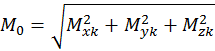
Понятие о статическом равновесии конструкции
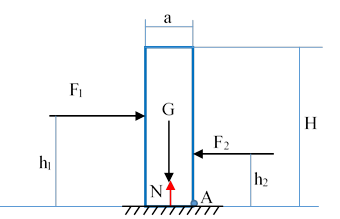
Составляется уравнение относительно точки опрокидывания конструкции
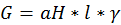 – вес стены
– вес стены
Точка А – точка возможного опрокидывания
![]()
![]()
![]()
Муд=1,5Мопр
Мопр – момент опрокидывающий
Муд – удерживающий момент
Приведение силы к произвольному центру по методу Пуансо
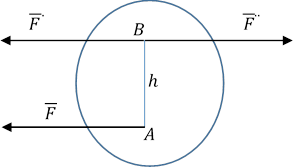 |
![]()
Чтобы эффект действия сохранился нужно добавить равную и противоположную силу ![]() , которая образует присоединенную пару с плечом AB.
, которая образует присоединенную пару с плечом AB.
В результате приведения получаем силу ![]() , равную исходной и присоединенную пару.
, равную исходной и присоединенную пару.
![]() с моментом M=Fh, можно представить в виде вектор – момента.
с моментом M=Fh, можно представить в виде вектор – момента.
Так как вектор – момент свободный вектор, то его так же можно построить в точке B. Следовательно получаем: 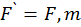 , которые можно приложить в точку B.
, которые можно приложить в точку B.
Применяя метод Пуансо к системе сил, произвольно расположенных в пространстве можно получить условие равновесия любой произвольной системы в пространстве.
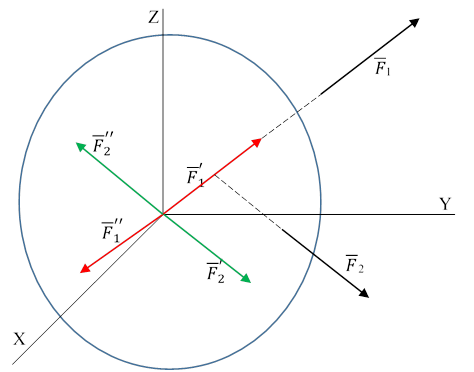 Приведение пространственной системы сил к произвольному центру.
Приведение пространственной системы сил к произвольному центру.
Условия равновесия пространственной системы
Требуется привести силы с центром О, с которым свяжем систему координат. Переносим F1 в точку О, прикладываем 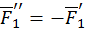 , которая образует пару, проделываем то же с F2.
, которая образует пару, проделываем то же с F2.
Т. к. вектор-моменты пар являются параллельными векторами все их можно приложить к точке О.
Складывая их геометрически получим главный вектор момент:
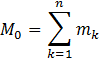
Складывая F1, F2, Fn получаем главный вектор:
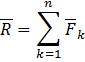
Ориентация векторов может быть определена с помощью косинусов.
Любую произвольную систему сил можно привести к любому центру и заменить двумя векторами M и R.


