Тепловлажностые характеристики

gв. п – массовая доля водяного пара, .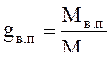

если массу сухого воздуха принять за 1 кг (Мс. в = 1 кг), а массу водяного пара выразить в килограммах через влагосодержание, и так как влагосодержание 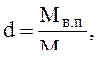тогда Мв. п = d·10 –3, отсюда следует, что масса влажного воздуха, кг,

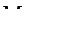
(9)

Мв. в = 1 + 30·10 –3 ≈ 1,03 кг, следовательно, в практических расчетах Мв. в можно принимать как массу влажного воздуха с точностью до 3 %, как массу сухого воздуха: Мв. в = Мс. в. (10)

объем влажного воздуха, м3, имеет такое же значение как сухой воздух и водяные пары, так как он всегда занимают конкретный объем (помещения, оборудования, воздуховодов и т. д):

Vв. в = Vс. в = Vв. п = V. (11)

плотность ρв. в, кг/м3,

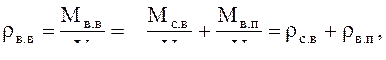(12.а)

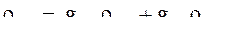(12.б)

так как массовая доля водяного пара мала, то в инженерных расчетах можно принять ρв. в ≈ ρс. в, (13)

но следует помнить, что ρв. в < ρс. в, так как молярная масса водяного пара μв. п = 18,016 кмоль, а молярная масса сухого воздуха μс. в = 28,29 кмоль.

удельный объем – из уравнения состояния влажного воздуха:

рв. вvв. в = Rв. в Тв. в, (14)

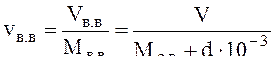. (15)

Следовательно, удельный объем влажного воздуха тоже можно принимать как удельный объем сухого воздуха, так как Мв. в = Мс. в. по формуле (9).

vв. в = vс. в. (16)

газовая постоянная влажного воздуха Rв. в, Дж/(кг·К),

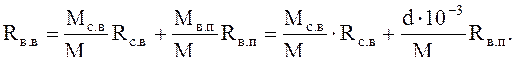
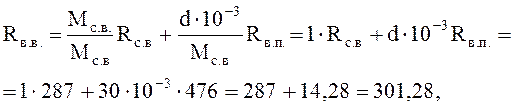
где Rс. в – газовая постоянная сухой части воздуха, Дж/(кг·К), Rс. в = 287;

Rв. п – газовая постоянная водяного пара, Дж/(кг·К), Rс. в = 476.

следовательно, в практических расчетах Rв. в можно принимать как газовую постоянную сухого воздуха, так как 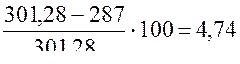меньше 5 %, что допустимо в инженерных расчетах.

Rв. в = Rс. в. (17)

Тепловлажностые характеристики

удельная изобарная теплоемкость св. в., кДж/(кг·К), которую относят к 1 килограмму сухого воздуха или к d·10 – 3 килограмму водяного пара, равна

св. в = 1·сс. в + (d·10 –3) св. п. (18.а)

для инженерных расчетов можно принять: св. в ≈ сс. в ≈ 1,008. (18.б)

удельная энтальпия iв. в, кДж/кг, которую тоже относят к 1 килограмму сухого воздуха или к d·10 – 3 килограмму водяного пара, равна:

iв. в = gс. в iс. в + gв. п iв. в = 1·iс. в + d·10 –3 iв. п, (19. а)

выразив удельные энтальпии через произведение удельной теплоемкости и температуры, получим:

iв. в = сс. в t + d·10 – 3(св. пt + r), (19. б)

где r – удельная теплота парообразования, кДж/кг.

В системе измерений СИ:

iв. в = 1,008·t + (d·10 –3)·(1,8·t + 2 500). (19. в)

i-d диаграмма влажного воздуха

Свойства влажного воздуха необходимо знать при вентиляции помещений с избыточными выделениями тепла и влаги, а также при исследовании процессов сушки материалов и для других инженерных задач.

все параметры влажного воздуха можно определить аналитически, но в проектной практике широкое распространение получил графический метод их определения с помощью i-d диаграммы влажного воздуха. Эта диаграмма была предложена профессором Л. К. Рамзиным в 1918 г. и широко применяется в расчетах систем вентиляции, отопления, кондиционирования воздуха (ВОК) и процессов сушки.

В основу построения диаграммы легли два уравнения (6) и (19в) – влагосодержания и удельной энтальпии влажного воздуха:

1)

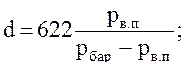
2) iв. в = 1,008·t + d·10 –3· (1,8·t + 2 500).

Диаграмма i-d графически связывает следующие параметры:

·  влагосодержание d, гв. п/(кгс. в);

·  удельную энтальпию. i, кДж/(кгс. в);

·  температуру, t °С;

·  относительную влажность φ, %;

·  парциальное давление водяных паров рв. п, кПа.

По оси абсцисс откладывается влагосодержание d, гв. п/(кгс. в), а по оси ординат – удельная энтальпия влажного воздуха i, кДж/(кгс. в), и температура t °С. за начало отсчета удельной энтальпии принята нулевая точка, в которой d = 0, i = 0, t = 0.

При построении диаграммы принята косоугольная система координат, так как в такой системе область ненасыщенного воздуха занимает большую площадь диаграммы. Через точки на оси ординат проводят линии постоянной удельной энтальпии (i = const) под углом 135 ° к линии постоянного влагосодержания (d = const). После нанесения сетки из линий i = const и d = const на диаграмму наносят линии постоянной температуры – изотермы (t = const) и кривые линии постоянной относительной влажности (φ = const). Уравнение энтальпии показывает, что изотермы – прямые линии. В нижней части диаграммы нанесена линия парциальный давлений водяного пара рв. п, кПа.

Кривая линия, соответствующая φ = 100 %, делит диаграмму на две части. Справа от линии расположена область влажного ненасыщенного воздуха, слева – область влажного насыщенного воздуха.

Два любых параметра определяют на диаграмме точку тепловлажностного состояния воздуха, по которой можно найти остальные параметры.

Обычно диаграмма строится для какого-то конкретного атмосферного давления. Но по этой диаграмме можно рассчитывать параметры влажного воздуха и для других атмосферных давлений воздуха, хотя линии относительных влажностей φ = const – неоднозначны. В этом случае

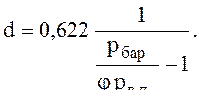(20)

отсюда вытекает, что любая кривая φ = const может быть использована для любых атмосферных давлений, но значения φ определяется отношением (рбар /φ).

Кроме того, по диаграмме можно найти параметры насыщения влажного воздуха:

1) парциальное давление насыщения водяными парами воздуха при t = const;

2) насыщенное влагосодержание водяными парами воздуха при данной температуре,

3) насыщенная энтальпия водяными парами воздуха, при данной температуре,

4) температуру точки росы tр – температуру насыщения при d = const;

5) температуру мокрого термометра tм – температуру насыщения при i = const.

По двум любым параметрам на диаграмму наносится точка, которая характеризует тепловлажностное состояние влажного воздуха и по этой точке можно определить все остальные параметры (рисунок 1).

Например возьмем точку с параметрами воздуха: t = 20 °С и j = 50 %.

Находим следующие параметры воздуха: i, кДж/кг, d, г/(кг с. в), рв. п, кПа, , tр, tм.

опускаясь от точки вниз по d = const до линии парциального давления водяного пара, далее по горизонтали определим парциальное давление водяного пара воздуха (рв. п), кПа. Для определения из точки идем по линии t = const до пересечения c линией φ = 100 %, а затем по d = const до пересечения со вспомогательной линией парциального давления водяного пара, далее по горизонтали определим парциальное давление насыщения водяного пара воздуха.

Движение от точки по i = const до шкалы энтальпий, определим удельную энтальпию, кДж/кг. Для определения из точки идем по линии t = const до пересечения c линией φ = 100 %, а затем по i = const до шкалы энтальпий.