Тесты теория упругости и пластичности

Тесты для проверки остаточных знаний

по курсу «Теория упругости и пластичности»

для студентов направления «Строительство»

профиля ПГС (3 г.)

!TASKFILE 01. Основные допущения и гипотезы теории упругости

!TYPE=2

!PERCENT=100

!TIME=1

!SPACE=5

СПЕЦИФИКАЦИЯ БАНКА ЗАДАНИЙ

1. Составители Петров В. В., Кривошеин И. В.

2. Предмет. Основы теории упругости и пластичности

3. Раздел ГОС. ОПД

4. Раздел рабочей программы

5. Тема. Основные допущения и гипотезы теории упругости

6. Уровень сложности. 2

7. Ориентировочное время выполнения. 1

8. Перечень контролируемых учебных элементов (УЭ):

Студент должен знать: а)

б)…

уметь: а)

б)…

9. Количество заданий в данном файле 7

!TASK1

Как формулируется гипотеза об идеальной упругости тела?

1. Идеально упругое твердое тело полностью восстанавливает первоначальные форму и объем после устранения внешних физических воздействий

2. Идеально упругое твердое тело восстанавливает первоначальные форму и объем после устранения внешних физических воздействий

3. Идеально упругое твердое тело полностью восстанавливает первоначальную форму после устранения внешних физических воздействий

4. Идеально упругое твердое тело полностью восстанавливает первоначальный объем после устранения внешних физических воздействий

!TASK2

Как формулируется гипотеза о естественном первоначальном состоянии твердого тела?

1. Естественным называется первоначальное состояние тела, если при отсутствии температурных перепадов в теле не возникает никаких напряжений

2. Естественным называется первоначальное состояние тела, если при отсутствии нагрузок в теле не возникает никаких напряжений

3. Естественным называется первоначальное состояние тела, если при отсутствии смещений опорных закреплений в теле не возникает никаких напряжений

4. Естественным называется первоначальное состояние тела, если при отсутствии его перемещений в теле не возникает никаких напряжений

!TASK3

Как формулируется гипотеза о сплошности идеально упругого тела?

1. Идеально упругое тело предполагается сплошном, то есть непрерывным как до деформирования, так и в процессе деформирования

2. Идеально упругое тело предполагается сплошном, то есть непрерывным в процессе деформирования и после процесса деформирования

3. Идеально упругое тело предполагается сплошном, то есть непрерывным как до деформирования, так и в процессе деформирования и после процесса деформирования

4. Идеально упругое тело предполагается сплошном, то есть непрерывным до деформирования

!TASK4

Как формулируется гипотеза об однородности твердого тела?

1. В однородном твердом теле во всех его точках возникают одинаковые деформации

2. В однородном твердом теле во всех его точках возникают одинаковые напряжения

3. В однородном твердом теле во всех его точках свойства одинаковы

4. В однородном твердом теле во всех его точках при одних и тех же напряжениях возникают одинаковые деформации

!TASK5

Как формулируется гипотеза об изотропности идеально упругого тела?

В изотропном идеально упругом теле упругие свойства тела в каждой его точке

одинаковы по всем направлениям

2. В изотропном идеально упругом теле упругие свойства тела одинаковы по всем

направлениям

3. В изотропном теле упругие свойства тела в каждой его точке одинаковы по

всем направлениям

4. В изотропном идеально упругом теле упругие свойства тела в каждой его точке

различны по различным направлениям

!TASK6

Как формулируется принцип независимости действия сил?

1. При малых перемещениях эффект от суммы воздействий на твердое идеально упругое

тело равен сумме эффектов от каждого воздействия в отдельности

2. Эффект от суммы воздействий на твердое тело равен сумме эффектов от

каждого воздействия в отдельности

3. Эффект от суммы воздействий на твердое идеально упругое тело может быть определен

как алгебраическая сумма эффектов от каждого воздействия в отдельности

4. При малых перемещениях эффект от суммы воздействий на твердое идеально упругое

тело равен алгебраической сумме эффектов от каждого воздействия в отдельности

!TASK7

Как формулируется принцип локальности эффекта самоуравновешенных нагрузок

Сен-Венана?

Замена распределенной нагрузки, приложенной к части тела, на эквивалентную ей

сосредоточенную силу не влияет на внутренние сила в идеально упругом твердом теле

Деформации идеально упругого твердого тела не меняются при переносе сил вдоль

линий их действия

Если систему сил, приложенную к небольшой площадке поверхности тела, заменить

другой системой, статически эквивалентной первой, то напряженно-деформированное

состояние тела не измениться, за исключением небольшой области, непосредственно

примыкающей к площадке, через которую передаются усилия

Деформации идеально упругого твердого тела не изменятся, если систему

сосредоточенных сил, приложенных к нему, заменить на одну сосредоточенную силу,

эквивалентную системе сил

!END

!TASKFILE 01. Фундаментальная система уравнений теории упругости

!TYPE=2

!PERCENT=100

!TIME=1

!SPACE=5

СПЕЦИФИКАЦИЯ БАНКА ЗАДАНИЙ

1. Составители Петров В. В., Кривошеин И. В.

2. Предмет. Основы теории упругости и пластичности

3. Раздел ГОС. ОПД

4. Раздел рабочей программы

5. Тема. Фундаментальная система уравнений теории упругости

6. Уровень сложности. 2

7. Ориентировочное время выполнения. 1

8. Перечень контролируемых учебных элементов (УЭ):

Студент должен знать: а)

б)…

уметь: а)

б)…

9. Количество заданий в данном файле 9

!TASK1

Какая из формул выражает уравнение равновесия в проекции на ось 0Z?

1.

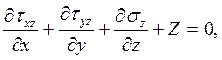
2.

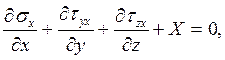
3.

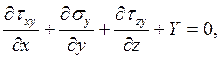
4.

!TASK2

Какая из формул выражает уравнение связи сдвиговой деформации в плоскости X0Y c компонентами вектора перемещения?

1.

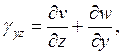
2.

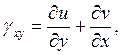
3.

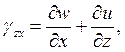
4.

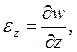
!TASK3

Какая из формул выражает уравнение неразрывности деформаций в плоскости X0Z?

1.

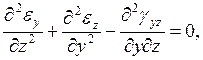
2.

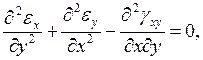
3.

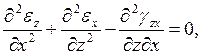
4.

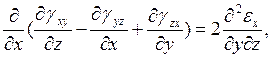
!TASK4

Какая из формул выражает уравнение обобщенного закона Гука связи деформации сдвига в плоскости Y0Z с компонентами тензора напряжения?

1.

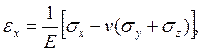
2.

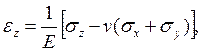
3.

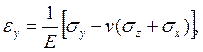
4.

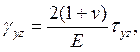
!TASK5

Какая из формул выражает закон парности касательных напряжений?

1.

2.

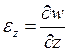
3.

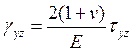
4.

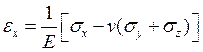
!TASK6

Какая из формул выражает уравнение связи линейной деформации в направлении оси 0Y c компонентами вектора перемещения?

1.

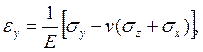
2.

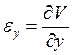
3.

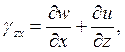
4.

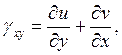
!TASK7

Какая из формул соответствует выражению для нормального напряжения по оси Y на наклонной площадке?

1.

2.

3.

4.

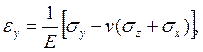
!TASK8

Какая из формул соответствует уравнению связи линейной деформации в направлении оси Y c угловыми деформациями в трех взаимно перпендикулярных плоскостях?

1.

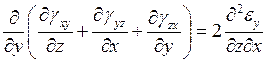
2.

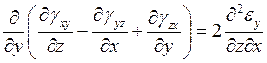
3.

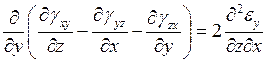
4.

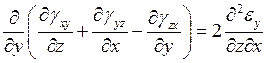
!TASK9

Какая из формул выражает уравнение обобщенного закона Гука связи линейной деформации в направлении оси 0X с компонентами тензора напряжения?

1.

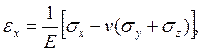
2.

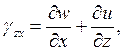
3.

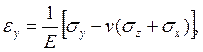
4.

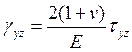
!END

!TASKFILE 01. О решении задачи теории упругости

!TYPE=2

!PERCENT=100

!TIME=1

!SPACE=5

СПЕЦИФИКАЦИЯ БАНКА ЗАДАНИЙ

1. Составители Петров В. В., Кривошеин И. В.

2. Предмет. Основы теории упругости и пластичности

3. Раздел ГОС. ОПД

4. Раздел рабочей программы

5. Тема. О решении задачи теории упругости

6. Уровень сложности. 2

7. Ориентировочное время выполнения. 1

8. Перечень контролируемых учебных элементов (УЭ):

Студент должен знать: а)

б)…

уметь: а)

б)…

9. Количество заданий в данном файле 9

!TASK1

Как преобразуются уравнения равновесия твердого тела при решении задачи теории упругости в перемещениях?

1. Путем выражения в данных уравнениях напряжений через перемещения.

2. Путем выражения в данных уравнениях напряжений через деформации

3. Путем выражения в данных уравнениях напряжений через интенсивность напряжений

4. Путем выражения в данных уравнениях напряжений через интенсивность деформаций

!TASK2

Как преобразуются условия на поверхности твердого тела при решении задачи теории упругости в перемещениях?

1. Путем выражения нормальных напряжений на наклонных площадках через деформации

2. Путем выражения нормальных напряжений на наклонных площадках через перемещения

3. Путем выражения нормальных напряжений на наклонных площадках через интенсивность деформаций

4. Путем выражения нормальных напряжений на наклонных площадках через интенсивность напряжений

!TASK3

Какую систему уравнений необходимо интегрировать при решении задачи теории упругости в напряжениях?

1. Три уравнения равновесия в проекции на оси X, Y, Z, записанные в напряжениях, и три уравнения неразрывности деформаций, записанные в напряжениях

2. Шесть уравнений равновесия в проекции на оси X, Y, Z, записанные в напряжениях, и три уравнения неразрывности деформаций, записанные в напряжениях

3. Три уравнения равновесия в проекции на оси X, Y, Z, записанные в напряжениях, и шесть уравнений неразрывности деформаций, записанные в напряжениях

4. Шесть уравнений равновесия в проекции на оси X, Y, Z, записанные в напряжениях, и шесть уравнений неразрывности деформаций, записанные в напряжениях

!TASK4

Дайте определение кинематической краевой задаче, определяемой граничными условиями на

поверхности тела.

1. Во внутренних точках тела отыскиваются перемещения, принимающие на поверхности тела определенные значения, для чего необходимо задать уравнение поверхности и значения

составляющих перемещений на этой поверхности

2. На поверхность тела не наложены никакие ограничения на перемещения, а задаются уравнение поверхности, направляющие косинусы нормали к поверхности и значения составляющих поверхностных нагрузок.

3. На поверхность тела не наложены никакие ограничения на перемещения, а задаются уравнение поверхности и значения составляющих поверхностных нагрузок.

4. В объеме тела отыскиваются составляющие перемещений, принимающие на поверхности тела определенные значения, для чего необходимо задать уравнение поверхности и значения

составляющих перемещений на этой поверхности

!TASK5

Дайте определение статической краевой задаче, определяемой граничными условиями на

поверхности тела.

1. На поверхность тела не наложены никакие ограничения на перемещения, а задаются уравнение поверхности, направляющие косинусы нормали к поверхности и значения составляющих поверхностных нагрузок.

2. Во внутренних точках тела отыскиваются перемещения, принимающие на поверхности тела определенные значения, для чего необходимо задать уравнение поверхности и значения

составляющих перемещений на этой поверхности

3. На поверхность тела не наложены никакие ограничения на перемещения, а задаются направляющие косинусы нормали к поверхности и значения составляющих поверхностных нагрузок.

4. В объеме тела отыскиваются составляющие перемещений, принимающие на поверхности тела определенные значения, для чего необходимо задать уравнение поверхности и значения

составляющих перемещений на этой поверхности

!TASK6

Дайте определение теоремы единственности решения задачи теории упругости для твердого тела

1. Если заданы объемные и поверхностные силы, действующие на упругое твердое тело, то решение задачи теории упругости для твердого тела единственно

2. Если заданы объемные и поверхностные силы, действующие на упругое твердое тело, или заданы перемещения на поверхности упругого тела, то решение задачи теории упругости для

твердого тела единственно

3. Если заданы перемещения на поверхности упругого тела, то решение задачи теории упругости для твердого тела единственно

4. Если заданы поверхностные силы, действующие на упругое твердое тело, или заданы перемещения на поверхности упругого тела, то решение задачи теории упругости для

твердого тела единственно

!TASK7

Дайте определение для прямого метода математического решения задачи теории упругости

1. При использовании прямого метода задаются функциями перемещений или напряжений, удовлетворяющих дифференциальным уравнениям, и определяют, каким внешним нагрузкам

соответствует рассматриваемая система перемещений или напряжений

2. При использовании прямого метода необходимо задать часть функций

напряжений или перемещений. Далее с помощью уравнений теории упругости устанавливаются зависимости, которым должны удовлетворять оставшиеся функции напряжений и перемещений.

3. Прямой метод заключается в непосредственном интегрировании уравнений теории упругости совместно с заданными условиями на поверхности

4. При использовании прямого метода задаются функциями перемещений, удовлетворяющих дифференциальным уравнениям, и определяют, каким внешним нагрузкам

соответствует рассматриваемая система перемещений

!TASK8

Дайте определение для обратного метода математического решения задачи теории упругости

1. Обратный метод заключается в непосредственном интегрировании уравнений теории упругости совместно с заданными условиями на поверхности

2. При использовании обратного метода необходимо задать часть функций

напряжений или перемещений. Далее с помощью уравнений теории упругости устанавливаются зависимости, которым должны удовлетворять оставшиеся функции напряжений и перемещений.

3. При использовании обратного метода задаются функциями перемещений или напряжений, удовлетворяющих дифференциальным уравнениям, и определяют, каким внешним нагрузкам

соответствует рассматриваемая система перемещений или напряжений

4. При использовании обратного метода задаются функциями напряжений, удовлетворяющих дифференциальным уравнениям, и определяют, каким внешним нагрузкам

соответствует рассматриваемая система напряжений

!TASK9

Дайте определение для полуобратного метода Сен-Венана математического решения задачи теории упругости

1. При использовании полуобратного метода Сен-Венана необходимо задать часть функций

напряжений или перемещений. Далее с помощью уравнений теории упругости устанавливаются зависимости, которым должны удовлетворять оставшиеся функции напряжений и перемещений.

2. При использовании полуобратного метода Сен-Венана необходимо задать часть функций

напряжений или перемещений. Далее с помощью уравнений равновесия устанавливаются зависимости, которым должны удовлетворять оставшиеся функции напряжений и перемещений.

3. Полуобратный метод заключается в непосредственном интегрировании уравнений теории упругости совместно с заданными условиями на поверхности

4. При использовании полуобратного метода задаются функциями перемещений или напряжений, удовлетворяющих дифференциальным уравнениям, и определяют, каким внешним нагрузкам соответствует рассматриваемая система перемещений или напряжений

!TASKFILE 01. Плоская задача теории упругости

!TYPE=2

!PERCENT=100

!TIME=1

!SPACE=5

СПЕЦИФИКАЦИЯ БАНКА ЗАДАНИЙ

1. Составители Петров В. В., Кривошеин И. В.

2. Предмет. Основы теории упругости и пластичности

3. Раздел ГОС. ОПД

4. Раздел рабочей программы

5. Тема. Плоская задача теории упругости

6. Уровень сложности. 2

7. Ориентировочное время выполнения. 1

8. Перечень контролируемых учебных элементов (УЭ):

Студент должен знать: а)

б)…

уметь: а)

б)…

9. Количество заданий в данном файле 9

!TASK1

Каковы условия возникновения плоской деформации в твердом теле?

1. Плоская деформация возникает, если перемещения происходят только параллельно плоскости X0Y:

2. Плоская деформация определяется напряженным состоянием вида: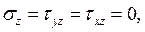

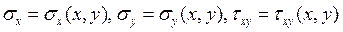
3. Плоская деформация определяется напряженным состоянием вида

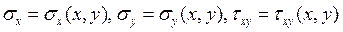
4. Плоская деформация возникает, если перемещения происходят только параллельно плоскости X0Y: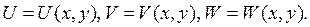

!TASK2

Какая из формул соответствует плоской деформации в плоскости X0Y?

1.

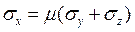
2.

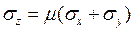
3.

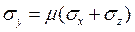
4.

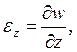
!TASK3

Какова математическая формулировка обобщенного плоского напряженного состояния в твердом теле?

1. Обобщенное плоское напряженное состояние возникает, если перемещения происходят только параллельно плоскости X0Y:

2. Обобщенное плоское напряженное состояние определяется напряженным состоянием вида:

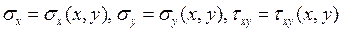
3. Обобщенное плоское напряженное состояние определяется напряженным состоянием вида

,

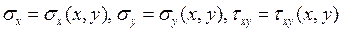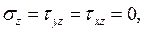
4. Обобщенное плоское напряженное состояние возникает, если перемещения происходят только параллельно плоскости X0Y:

!TASK4

Какая из формул соответствует обобщенному плоскому напряженному состоянию в

плоскости X0Y?

1.

2.

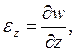
3.

4.

!TASK5

Как выражаются напряжения через функцию напряжений Эри?

1.

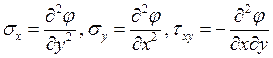
2.

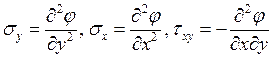
3.

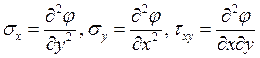
4.

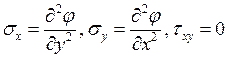
!TASK6

Как записывается бигармоническое уравнение плоской задачи теории упругости?

1.

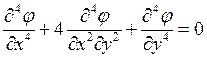
2.

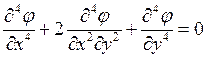
3.

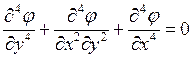
4.

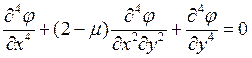
!TASK7

Какая из функций Эри не может быть принята для решения плоской задачи теории упругости?

1.

2.

3.

4.

!TASK8

Как записывается решение обыкновенного дифференциального уравнения (вертикальное направление) при расчете балки-стенки в одинарных тригонометрических рядах?

1.

2.

3.

4.

!TASK9

По какой формуле определяется радиальное нормальной напряжение в полуплоскости от действия сосредоточенной силы на ее границе?

1.

2.

3.

4.

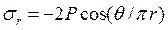
!END

!TASKFILE 01. Расчет упругих пластин по технической теории Навье

!TYPE=2

!PERCENT=100

!TIME=1

!SPACE=5

СПЕЦИФИКАЦИЯ БАНКА ЗАДАНИЙ

1. Составители Петров В. В., Кривошеин И. В.

2. Предмет. Основы теории упругости и пластичности

3. Раздел ГОС. ОПД

4. Раздел рабочей программы

5. Тема. Расчет упругих пластин по технической теории Навье

6. Уровень сложности. 2

7. Ориентировочное время выполнения. 1

8. Перечень контролируемых учебных элементов (УЭ):

Студент должен знать: а)

б)…

уметь: а)

б)…

9. Количество заданий в данном файле 12

!TASK1

Сформулируйте гипотезу прямых нормалей при изгибе тонких пластин

1. Любой прямолинейный элемент, нормальный к срединной плоскости до деформации, остается прямолинейным и нормальным к срединной поверхности после деформирования пластинки, и длина его не изменяется.

2. Любой прямолинейный элемент, нормальный к срединной плоскости до деформации, остается нормальным к срединной поверхности после деформирования пластинки, и длина его не изменяется.

3. Любой прямолинейный элемент, нормальный к срединной плоскости до деформации, остается прямолинейным и длина его не изменяется.

4. Любой прямолинейный элемент, нормальный к срединной плоскости до деформации, остается прямолинейным и нормальным к срединной поверхности после деформирования пластинки

!TASK2

Сформулируйте гипотезу о недеформируемости срединной плоскости пластинки

1. В срединной поверхности пластинки отсутствуют деформации растяжения, сжатия и сдвига, то есть она является нейтральной и ее перемещения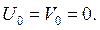

2. В срединной плоскости пластинки отсутствуют деформации растяжения, сжатия и сдвига, то есть она является нейтральной и ее перемещения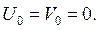

3. В срединной плоскости пластинки отсутствуют деформации сдвига, то есть она является нейтральной и ее перемещения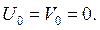

4. В срединной плоскости пластинки отсутствуют деформации растяжения и сжатия, то есть она является нейтральной и ее перемещения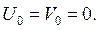

!TASK3

Сформулируйте гипотезу об отсутствии давления между слоями пластинки, параллельными срединной плоскости

1. Нормальные напряжения на площадках, параллельных срединной поверхности тонкой оболочки, равны нулю

2. Нормальные напряжения на площадках, параллельных срединной плоскости тонкой пластинки, могут быть выражены через нормальные напряжения в срединной поверхности пластинки

3. Нормальные напряжения на площадках, параллельных срединной плоскости тонкой пластинки, пренебрежимо малы по сравнению с прочими напряжениями

4. Нормальные напряжения на площадках, параллельных срединной плоскости тонкой пластинки, находятся из решения уравнения равновесия пластинки

!TASK4

Какая формула соответствует дифференциальному уравнению равновесия элемента пластины С. Жермен?

1.

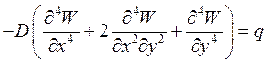
2.

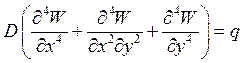
3.

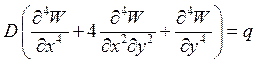
4.

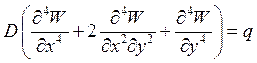
!TASK5

Какими формулами выражаются условия жесткого защемления прямоугольной пластины по всему ее контуру?

1.

2.

3.

4.

!TASK6

Какими формулами выражаются условия шарнирного опирания прямоугольной пластины по всему ее контуру?

1.

2.

3.

4.

!TASK7

Каким методом нельзя рассчитать прямоугольную пластину с одной защемленной и тремя шарнирно опертыми сторонами контура?

1. Методом Леви

2. Методом Ритца-Тимошенко

3. Методом Навье

4. Методом Бубнова-Галеркина

!TASK8

В каких точках прямоугольной пластинки при ее изгибе возникают наибольшие нормальные напряжения?

1. На нейтральной плоскости

2. Равномерно распределены по сечению

3. В центральной точке пластины

4. В точках на поверхности пластинки, наиболее удаленных от ее нейтральной плоскости

!TASK9

Как формулируется теорема возможных работ Лагранжа?

1. Если тело находится в равновесии, то сумма работ всех внешних и внутренних сил на любом возможном бесконечно малом перемещении равна нулю

2. Если тело находится в равновесии, то сумма работ всех внутренних сил на любом возможном бесконечно малом перемещении равна нулю

3. Если тело находится в равновесии, то сумма работ всех внешних сил на любом возможном бесконечно малом перемещении равна нулю

4. Если тело находится в равновесии, то сумма работ всех внешних и внутренних сил на любом возможном перемещении равна нулю

!TASK10

Как формулируется теорема Лагранжа-Дирихле?

1. Если состояние тела устойчиво, то его полная энергия минимальна

2. Если состояние тела устойчиво, то его полная потенциальная энергия минимальна

3. Если состояние тела устойчиво, то его полная потенциальная энергия принимает экстремальное значение

4. Если состояние тела устойчиво, то его полная потенциальная энергия максимальна

!TASK11

Использование какого метода расчета пластинок сводится к решению неоднородных обыкновенных дифференциальных уравнений?

1. Метода Бубнова-Галеркина

2. Метода Ритца-Тимошенко

3. Метода Власова-Канторовича

4. Метода Навье

!TASK12

Какая формула соответствует записи дифференциального уравнения равновесия пластинки, сжатой усилиями на контуре, распределенными по всем сторонам контура?

1.

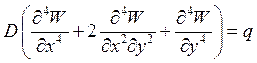
2.

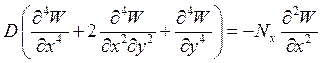
3.

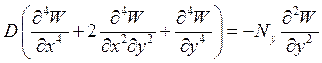
4.

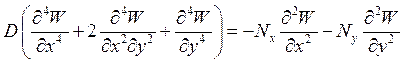
!END

!TASKFILE 01. Расчет пологих упругих оболочек

!TYPE=2

!PERCENT=100

!TIME=1

!SPACE=5

СПЕЦИФИКАЦИЯ БАНКА ЗАДАНИЙ

1. Составители Петров В. В., Кривошеин И. В.

2. Предмет. Основы теории упругости и пластичности

3. Раздел ГОС. ОПД

4. Раздел рабочей программы

5. Тема. Расчет пологих упругих оболочек

6. Уровень сложности. 2

7. Ориентировочное время выполнения. 1

8. Перечень контролируемых учебных элементов (УЭ):

Студент должен знать: а)

б)…

уметь: а)

б)…

9. Количество заданий в данном файле 7

!TASK1

Как формулируется гипотеза о прямолинейном элементе, нормальном к срединной поверхности тонкой оболочки?

1. Прямолинейный элемент, перпендикулярный срединной поверхности до деформации, остается прямым и перпендикулярным деформированной срединной поверхности и не изменяет своей длины

2. Прямолинейный элемент, перпендикулярный срединной поверхности до деформации, остается перпендикулярным деформированной срединной поверхности и не изменяет своей длины

3. Прямолинейный элемент, перпендикулярный срединной поверхности до деформации, остается прямым и перпендикулярным деформированной срединной поверхности

4. Прямолинейный элемент, перпендикулярный срединной поверхности до деформации, остается прямым и не изменяет своей длины

!TASK2

Как формулируется гипотеза о нормальных напряжениях на площадках, параллельных срединной поверхности тонкой оболочки?

1. Нормальные напряжения на площадках, параллельных срединной поверхности тонкой оболочки, равны нулю

2. Нормальные напряжения на площадках, параллельных срединной поверхности тонкой оболочки, пренебрежимо малы по сравнению с прочими напряжениями

3. Нормальные напряжения на площадках, параллельных срединной поверхности тонкой оболочки, могут быть выражены через нормальные напряжения в срединной поверхности оболочки

4. Нормальные напряжения на площадках, параллельных срединной поверхности тонкой оболочки, находятся из решения уравнений равновесия оболочки

!TASK3

Какими геометрические соотношения определяют пологие оболочки по теории В. З. Власова?

1. Стрела подъема оболочки над планом ее контура не должна превышать 1/4 минимального

размера оболочки в плане

2. Стрела подъема оболочки над планом ее контура не должна превышать 1/8 минимального

размера оболочки в плане

3. Стрела подъема оболочки над планом ее контура не должна превышать 1/5 минимального

размера оболочки в плане

4. Стрела подъема оболочки над планом ее контура не должна превышать 1/6 минимального

размера оболочки в плане

!TASK4

Какое условие не является условием безмоментности напряженного состояния оболочки?

1. Нагрузка на оболочку меняется плавно вдоль криволинейных координат срединной поверхности оболочки

2. Кривизны срединной поверхности оболочки не имеют разрывов второго рода

3. На контуре оболочки опорные устройства не препятствуют перемещениям оболочки по нормали к ее поверхности

4. Стрела подъема оболочки над планом ее контура должна быть не более 1/5 от минимального размера оболочки в плане

!TASK5

Как записывается уравнение неразрывности деформаций для пологой оболочки при малых прогибах (смешанный метод)?

1.

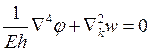
2.

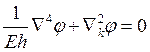
3.

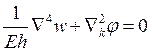
4.

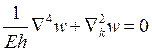
!TASK6

Как записывается уравнение равновесия в проекции на нормаль к поверхности пологой оболочки при малых прогибах (смешанный метод)?

1.

2.

3.

4.

!TASK7

Состояние равновесия упругой пологой оболочки устойчиво, если оболочка…

1. Продолжает деформироваться в направлении вызванного малого отклонения

2. Находится в безразличном равновесии: может сохранять как первоначальную форму равновесия, но может и потерять ее от любого малого воздействия

3. При любом малом отклонении от состояния равновесия стремится возвратиться к первоначальному состоянию после снятия воздействия, вызывающего данное малое отклонение

4. При любом малом отклонении от состояния равновесия совершает гармонические колебания вокруг первоначального состояния равновесия

!TASKFILE 01. Расчеты при пластических деформациях

!TYPE=2

!PERCENT=100

!TIME=1

!SPACE=5

СПЕЦИФИКАЦИЯ БАНКА ЗАДАНИЙ

1. Составители Петров В. В., Кривошеин И. В.

2. Предмет. Основы теории упругости и пластичности

3. Раздел ГОС. ОПД

4. Раздел рабочей программы

5. Тема. Расчеты при пластических деформациях

6. Уровень сложности. 2

7. Ориентировочное время выполнения. 1

8. Перечень контролируемых учебных элементов (УЭ):

Студент должен знать: а)

б)…

уметь: а)

б)…

9. Количество заданий в данном файле 7

!TASK1

Какое из нижеприведенных определений полностью определяет понятие пластичности

1. Пластичностью называется свойство твердого тела изменять под внешними воздействиями, не разрушаясь, свою форму и размеры и сохранять остаточные (пластические) деформации после устранения этих воздействий

2. Пластичностью называется свойство твердого тела изменять под внешними воздействиями свою форму и размеры и сохранять остаточные (пластические) деформации после устранения этих воздействий

3. Пластичностью называется свойство твердого тела изменять под внешними воздействиями, не разрушаясь, свою форму и сохранять остаточные (пластические) деформации после устранения этих воздействий

4. Пластичностью называется свойство твердого тела изменять под внешними воздействиями, не разрушаясь, свои размеры и сохранять остаточные (пластические) деформации после устранения этих воздействий

!TASK2

Как можно определить активное пластическое деформирование твердого тела?

1. Деформирование элемента тела в данный момент называется активным, если интенсивность

напряжений имеет значение, превышающее все предыдущие ее значения

2. Деформирование элемента тела в данный момент называется активным, если интенсивность

напряжений имеет значение, превышающее по модулю все предыдущие ее значения

3. Деформирование элемента тела в данный момент называется активным, если интенсивность

напряжений меньше хотя бы одного из предыдущих значений

4. Деформирование элемента тела в данный момент называется активным, если интенсивность

напряжений имеет постоянное значение

!TASK3

Какая из приведенных формулировок отвечает определению простого нагружения?

1. При простом процессе нагружения внешние силы с самого начала их приложения действуют одновременно, сохраняя между собой соотношение, изменяющееся пропорционально заданному параметру

2. При простом процессе нагружения активные силы с самого начала их приложения возрастают одновременно, сохраняя между собой постоянное соотношение, изменяясь пропорционально общему параметру

3. При простом процессе нагружения внешние силы с самого начала их приложения возрастают одновременно, сохраняя между собой постоянное соотношение, изменяясь пропорционально общему параметру

4. При простом процессе нагружения внешние силы возрастают одновременно с ростом некоторого параметра, зависящего от достигнутого уровня максимальной интенсивности напряжений

!TASK4

Как формулируется теорема А. А. Ильюшина о разгрузке?

1. Перемещения тела в некоторый момент стадии разгрузки отличаются от перемещений в момент начала разгрузки на величины упругих перемещений, которые возникли бы в теле,

если бы в естественном состоянии к нему были приложены внешние силы, равные разности внешних сил, действующих на тело в указанные моменты.

2. Перемещения точки тела в любой момент отличаются от перемещений в момент начала разгрузки на величины упругих перемещений, которые возникли бы в теле,

если бы в естественном состоянии к нему были приложены внешние силы, равные разности внешних сил, действующих на тело в указанные моменты.

3. Перемещения точки тела в некоторый момент стадии разгрузки отличаются от перемещений в момент начала разгрузки на величины перемещений, которые возникли бы в теле,

если бы в естественном состоянии к нему были приложены внешние силы, равные разности внешних сил, действующих на тело в указанные моменты.

4. Перемещения точки тела в некоторый момент стадии разгрузки отличаются от перемещений в момент начала разгрузки на величины упругих перемещений, которые возникли бы в теле,

если бы в естественном состоянии к нему были приложены внешние силы, равные разности внешних сил, действующих на тело в указанные моменты.

!TASK5

Как формулируется закон изменения объема в теории малых упругопластических деформаций А. А. Ильюшина?

1. При упругопластическом активном и пассивном деформировании объемная деформация твердого тела всегда является упругой и подчиняется закону Гука

2. При упругопластическом активном деформировании объемная деформация твердого тела всегда является упругой и подчиняется закону Гука

3. При упругопластическом активном и пассивном деформировании деформация твёрдого тела всегда является упругой и подчиняется закону Гука

4. При упругопластическом активном и пассивном деформировании объемная деформация твердого тела всегда является нелинейной функцией от напряжений

!TASK6

Как формулируется закон изменения формы в теории малых упругопластических деформаций А. А. Ильюшина?

1. При упругопластическом деформировании в процессе простого нагружения направляющие тензоры напряжений и деформаций совпадают

2. При активном упругопластическом деформировании в процессе простого нагружения направляющие тензоры напряжений и деформаций совпадают

3. При активном упругопластическом деформировании направляющие тензоры напряжений и деформаций совпадают

4. При активном упругопластическом деформировании в процессе простого нагружения тензоры напряжений и деформаций совпадают

!TASK7

Как формулируется закон о единой кривой деформирования в теории малых упругопластических деформаций А. А. Ильюшина?

1. Интенсивность напряжений является вполне определенной функцией интенсивности деформаций независимо от вида напряженного состояния

2. Интенсивность напряжений при активном деформировании данного материала является степенной функцией интенсивности деформаций независимо от вида напряженного состояния

3. Интенсивность напряжений при активном деформировании данного материала является вполне определенной функцией интенсивности деформаций независимо от вида напряженного состояния

4. Интенсивность напряжений при активном деформировании данного материала является функцией интенсивности деформаций независимо от вида напряженного состояния