Требования, предъявляемые к зубчатым зацеплениям

Недостатками этих передач являются: сравнительно высокая трудоёмкость изготовления колёс, возможность появления шума в процессе работы и некоторые др.

Процесс передачи движения с помощью зубьев принято называть зубчáтым зацеплением.

Передачи классифицируют по геометрическим и функциональным особенностям.

1. По взаимному расположению осей колёс:

– цилиндрические передачи (оси колёс – параллельны (рис. 51 а));

– конические передачи (оси колёс пересекаются, (рис.51 б));

-гиперболоидные передачи (оси колёс перекрещиваются, (рис. 51 в));

– реечная передача (рис. 52 а).

2. По относительному расположению поверхностей вершин и впадин зубьев колёс:

– передачи внешнего зацепления (образуются при зацеплении колёс с внешними зубьями, (рис. 51 а));

– передачи внутреннего зацепления (образуются при зацеплении колёс, одно из которых имеет внутренние зубья, (рис. 52 б));

3. По направлению зубьев:

– передачи с прямыми зубьями (прямозубые);

– передачи с криволинейными зубьями.

4. По характеру движения осей:

– обычные (рядовые) передачи:

– планетарные (с подвижными осями одного или нескольких колёс) передачи.

5. По профилю зубьев:

– передачи с эвольвентным зацеплением (профили зубьев очерчены эвольвентами окружностей);

– передачи с циклоидальным (от греч. kykloeides – кругообразный, круглый) зацеплением; профили зубьев в этом зацеплении выполнены по дугам эпи — и гипоциклоид (эпи от греч. επι –префикс «на» и гипо от греч. ΰπο – префикс «под»);

–передачи с зацеплением Новикова (профили выполнены дугами окружностями, причём выпуклый профиль зуба одного колеса взаимодействует с вогнутым профилем зуба другого колеса).

6. В зависимости от наличия смазки:

– открытые передачи (передачи, работающие без смазки или с ограниченной смазкой);

– закрытые передачи (передачи, работающие с обильной смазкой).

Зубчатые передачи могут понижать или повышать частоту вращения ведомого вала. Зубчатые механизмы, служащие для уменьшения числа оборотов выходного вала по сравнению с входным, называются редукторами (от лат. reduktor – отводящий назад, приводящий обратно), а механизмы, служащие для увеличения числа оборотов выходного вала, называются мультипликаторами (от лат.multiplico – умножаю, увеличиваю).

6.2. Требования, предъявляемые к зубчатым зацеплениям

Зацепление, применяющееся в зубчатых передачах, должно обеспечить:

1. Постоянство передаточного отношения (i=ωвх/ωвых).

2. Небольшие габариты передачи при больших значениях передаточного отношения.

3. Минимальное трение в зацеплении.

4. Небольшую чувствительность к неизбежным погрешностям изготовления и монтажа.

5. Безударную работу и плавное вхождение зубьев в зацепление.

6. Малый боковой зазор в передаче для исключения или значительного снижения люфтовой (от нем. die Luft – зазор) погрешности.

7. Возможность правильного зацепления колёс одного модуля при разных числах колёс.

8. Высокий КПД.

9. Высокую технологичность изготовления и контроля.

10. Достаточную прочность зуба.

В настоящее время нет зацепления, которое бы в полной мере удовлетворяло всем перечисленным требованиям. Наилучшим образом удовлетворяет этим требованием (1, 4, 5, 6, 7, 8, 9, 10) эвольвентное зацепление, предложенное Л. Эйлером в 1760 г.

6.3. Основной закон зацепления

Как было сказано, важнейшим требованием, предъявляемым к передачам, является постоянство передаточного отношения в любой момент зацепления пары колёс. Передача движения в зубчатых колёсах происходит нажатием зуба одного колеса на зуб другого. Какими же должны быть профили зубьев колёс, чтобы передаточное отношение было строго постоянным. Ответ на этот вопрос даёт основной закон зацепления который формулируется следующим образом: общая нормаль n – n (рис. 53), проведенная в точке С касания зубьев 1 и 2, делит межосевое расстояние О1О2 в точке Р на отрезки О1Р и РО2, обратно пропорциональные угловым скоростям ω1 и ω2:

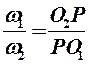. (69)

Из равенства (69) следует: для обеспечения постоянства передаточного отношения необходимо, чтобы отрезки О1Р и РО2, на которые нормаль n – n делит межосевое расстояние О1О2, были постоянной величины, т. е.

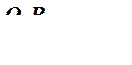(70)

Другими словами, необходимо, чтобы нормаль n – n всегда, в любом положении звеньев, проходила через одну и ту же точку Р.

Все кривые, удовлетворяющие этому условию, могут быть использованы в качестве профилей зубьев. Такие кривые называются сопряжёнными. Задаваясь произвольно профилем зуба одного колеса, можно построить сопряжённый профиль зуба другого колеса. Таких кривых может быть теоретически бесконечное множество. Однако на практике в подавляющем большинстве случаев пользуются эвольвентным зацеплением, в котором боковые профили зубьев колёс выполнены по эвольвентным кривым.

6.4. Эвольвента окружности и её свойства. Уравнения эвольвенты

Эвольвентой (от лат. evolvens (evolventis) – разворачивающий) или развёрткой окружности называют плоскую кривую А0Y (рис. 54), которая описывается любой точкой Y прямой n—n, перекатываемой без скольжения по окружности. Линию n—n называют производящей прямой, а окружность радиуса rb, по которой она перекатывается, – эволютой (от лат. evoluta – развёртка) или основной окружностью.

Основные свойства эвольвенты:

– образующая прямая n – n всегда нормальна к эвольвенте (основное и важнейшее свойство эвольвенты);

– эвольвента начинается на основной окружности и всегда расположена вне окружности;

– форма эвольвенты зависит только от радиуса основной окружности;

– эвольвента является кривой без перегибов.

Уравнение эвольвенты. Положение какой-либо точки Y эвольвенты определяется радиус-вектором ry и углом θy, называемым эвольвентным. Из свойства эвольвенты следует, что

NY=˘NmA0. (71)

Из рис. 54 видно, что

NY=rbtgαY, (72)

где α – угол профиля (угол между радиус-вектором ry и касательной к эвольвенте в точке А);

˘NmA0 = rb∙νY, (73)

где ν – угол развёрнутости (νy=αy+θy).

Подставляя (72) и (73) в (71), получаем

rbtgαy= rb∙νy= rb(αy+θy)

или

tgαy = (αy+θy). (74)

Из (8.6) находим

Θy = tgαy–αy. (75)

Выражение tgαY–αY сокращённо обозначается знаком invαY и читается как инволюта αY (от лат. involuta – развёрнута – то же самое, что и эвольвента): tgαY–αY = invαY.