Уравнение неразрывности

4.2. Уравнение неразрывности (сплошности)

а) Для элементарной струйки

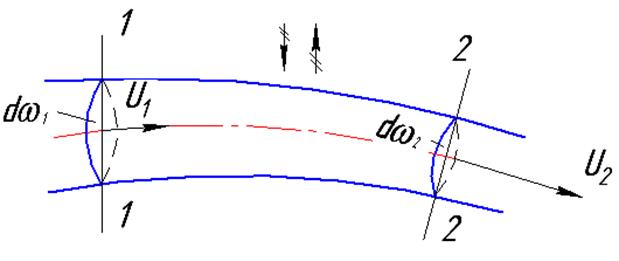
Рис.4.7

В элементарной струйке переменного сечения (рис.4.7) выберем два произвольных сечения 1-1 и 2-2 с живыми сечениями и . Так как жидкость является сплошной средой (без пустот и переуплотнений) и приток и отток жидкости вдоль струйки отсутствуют, то для несжимаемой жидкости можно предположить, что объемные расходы через сечения 1-1 и 2-2 должны быть равны между собой:

dQ1 = dQ2 = сonst или (4.1)

U1dw1 = U2dw2 = сonst. (4.2)

уравнения (4.1), (4.2) называют уравнениями неразрывности, или сплошности.

Из уравнения (4.2) можно получить:

.

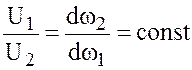б) Для потока

Аналогичное уравнение можно составить и для потока, ограниченного непроницаемыми стенками, только вместо истинных скоростей ввести средние скорости:

Q1 = Q2 = const; V1·ω1 = V2·ω2 = const; .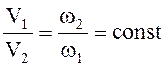

4.3. Уравнение Д. Бернулли для элементарной струйки

идеальной жидкости. График уравнения Д. Бернулли

Это уравнение является основным в гидродинамике. Оно устанавливает связь между давлением, скоростью и положением жидкости в пространстве и может быть получено аналитически только для случая движения идеальной жидкости, т. е. жидкости, лишенной всех свойств реальной жидкости (абсолютно несжимаема и нерасширяема, а главное, абсолютно подвижна, т. е. лишена вязкости). Такой жидкости в природе не существует. Близок к ней жидкий гелий при температуре 2оК.

Представим себе элементарную струйку переменного сечения (рис.4.8).

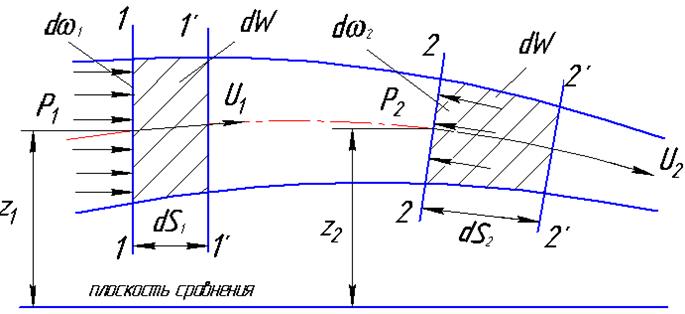
Рис.4.8

Двумя сечениями 1-1 и 2-2 с живыми сечениями d1 и d2 выделим отсек жидкости 1-1-2-2. допустим, что за бесконечно малое время dt этот отсек сдвинулся и занял новое положение 1′-1′-2′-2′. Живые сечения при этом переместились соответственно на расстояния ds1 и ds2.

Из рисунка 4.8 видно, что никакого изменения в пространстве не получил отсек жидкости 1′-1′-2-2, при движении он не совершил никакой работы, т. е. отсек жидкости 1-1-1′-1′ с высоты Z1 как бы переместился до высоты Z2 и занял положение 2-2-2′-2′ (на рисунке они заштрихованы).

На основании уравнения неразрывности делаем вывод, что массы жидкости в этих отсеках равны между собой, а скорость в сечении 2-2 по сравнению с сечением 1-1 возросла, т. е. произошло изменение кинетической энергии.

Для вывода этого уравнения используем известную из механики теорему об изменении кинетической энергии. Напомним, что эта теорема читается так:

изменение кинетической энергии 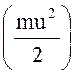рассматриваемого тела на некотором его перемещении равно сумме работ от внешних сил, приложенных к данному телу на том же перемещении.

Какие же силы действуют в нашем случае?

Это силы тяжести и силы давления. Согласно упомянутой выше теореме можно записать:

dT=AG+Ap, (4.3)

где dT – изменение кинетической энергии; AG — работа от сил тяжести; Ap — работа от сил давления.

Изменение кинетической энергии

dT=.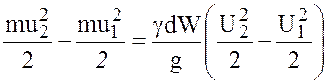

Работа от сил тяжести

.

Работа от сил давления

.

Сделаем подстановку составляющих в выражение (4.3):

.

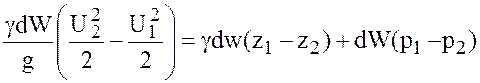
Разделим каждое слагаемое на и сгруппируем:

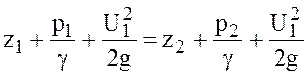. (4.4)

Выражение (4.4) является расчетной формой уравнения Бернулли, т. е. в такой форме оно составляется при решении различных задач.

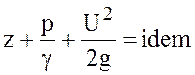. (4.5)

Выражение (4.5) является общей формой уравнения Бернулли.

Каждый из членов этого уравнения имеет линейную размерность и называется «напор», т. е. это удельная энергия, а удельная энергия – это энергия единицы веса жидкости, т. е. одного ньютона.

В формуле (4.5):

z– геометрический напор, или удельная потенциальная энергия положения;

— пьезометрический напор, или удельная потенциальная энергия давления;

— скоростной напор, или удельная кинетическая энергия.

Сумма перечисленных напоров составляет гидродинамический напор:

Нг. д = z++.

Физический смысл уравнения Бернулли заключается в том, что оно является уравнением закона сохранения энергии для движущейся жидкости.

Для лучшего понимания смысла полученного уравнения (4.4) представим его графически (рис.4.9).

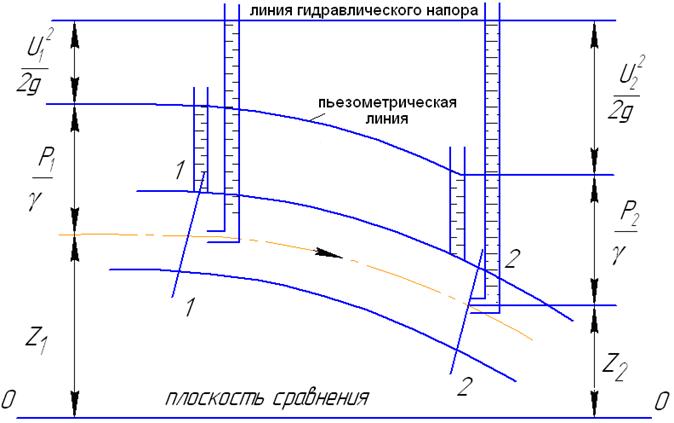
Рис.4.9

4.4. Уравнение Д. Бернулли для элементарной струйки

реальной жидкости. График уравнения Д. Бернулли

В отличие от идеальной жидкости, в которой работа внешних сил, действующих на жидкость, полностью идет на изменение ее кинетической энергии, благодаря чему происходит преобразование кинетической энергии в потенциальную или наоборот, в реальной жидкости, обладающей вязкостью, часть работы сил, действующих на жидкость, затрачивается на преобразование механической энергии в тепловую.

Если преобразование одной формы механической энергии в другую форму механической энергии является процессом обратимым, то преобразование механической энергии в тепловую, происходящее вследствие сил трения, является процессом необратимым.

Это явление, называемое диссипацией энергии, в гидравлике рассматривается как гидравлическое сопротивление, а величина диссипируемой энергии называется гидравлическими потерями. Явление диссипации в движущейся жидкости чрезвычайно сложно, поэтому вывести уравнение для реальной жидкости не представляется возможным, но можно написать уравнение баланса энергии. Его расчетная форма имеет вид

z1++= z1+++hп, (4.6)

где hп – гидравлические потери.

Уравнение (4.6) представим графически (рис.4.10).

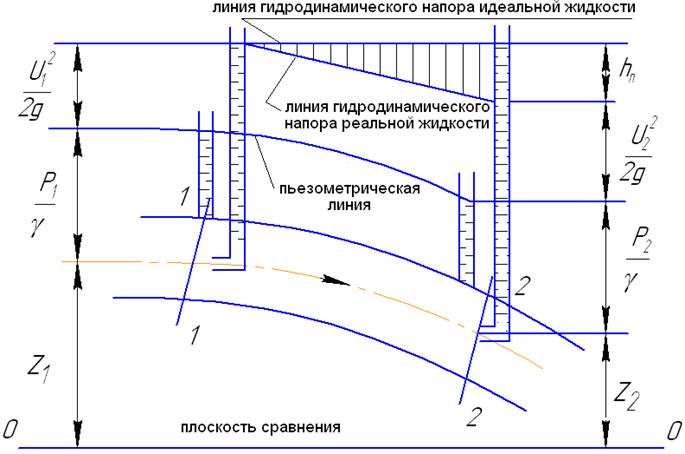
Рис.4.10

4.5. Уравнение Д. Бернулли для потока реальной жидкости

Так как поток представлен совокупностью элементарных струек, то его энергия должна быть равна сумме энергий этих струек.

Удельная энергия элементарной струйки

е =z++, м.