ВУЗы по физике
Готовые работы по физике
Как писать работы по физике
Примеры решения задач по физике
Решить задачу по физике онлайнУравнения математической физики ргр
УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
Задания для расчётно-графической работы
Задача 1. Определить тип уравнения и привести его к каноническому виду.
|
1.1. |
1.2. |
|
1.3. |
1.4. |
|
1.5. |
1.6. |
|
1.7. |
1.8. |
|
1.9. |
1.10. |
|
1.11. |
1.12. |
|
1.13. |
1.14. |
|
1.15. |
1.16. |
|
1.17. |
1.18. |
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.Задача 2. Найти решение 
уравнения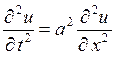 
, удовлетворяющее начальным условиям
, 
, 
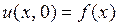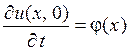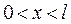
и граничным условиям
, 
, 
,
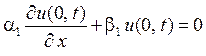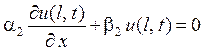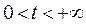где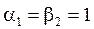 
, 
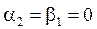для нечётных вариантов; 
, 
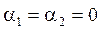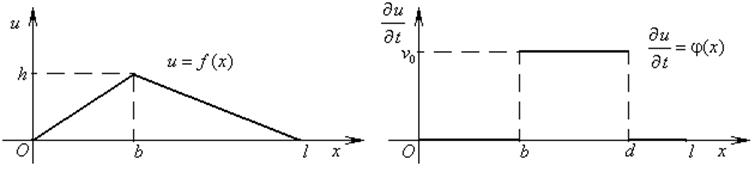
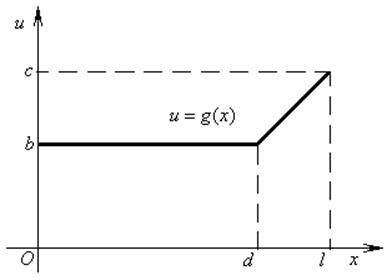
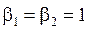для чётных вариантов. Вид функций 
и 
изображён на рисунках.
|
|
|
№ |
|
|
|
|
№ |
|
|
|
|
|
2.1. |
1,00 |
0,02 |
0,0098 |
0,42 |
2.2. |
2,00 |
0,08 |
0,0768 |
0,88 |
|
2.3. |
3,00 |
0,18 |
0,2538 |
1,38 |
2.4. |
4,00 |
0,32 |
0,5888 |
1,92 |
|
2.5. |
5,00 |
0,50 |
1,1250 |
2,50 |
2.6. |
1,00 |
0,12 |
0,0528 |
0,52 |
|
2.7. |
2,00 |
0,28 |
0,2408 |
1,08 |
2.8. |
5,00 |
2,90 |
3,0450 |
4,90 |
|
2.9. |
4,00 |
0,72 |
1,1808 |
2,32 |
2.10. |
5,00 |
0,90 |
1,8450 |
2,90 |
|
2.11. |
1,00 |
0,22 |
0,0858 |
0,62 |
2.12. |
2,00 |
0,48 |
0,3648 |
1,28 |
|
2.13. |
3,00 |
0,78 |
0,8658 |
1,98 |
2.14. |
4,00 |
1,12 |
1,6128 |
2,72 |
|
2.15. |
5,00 |
1,50 |
2,6250 |
3,50 |
2.16. |
1,00 |
0,32 |
0,1088 |
0,72 |
|
2.17. |
2,00 |
0,68 |
0,4488 |
1,48 |
2.18. |
3,00 |
1,08 |
1,0368 |
2,28 |
Задача 3. Методом Фурье найти решение 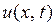уравнения 
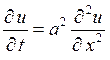, удовлетворяющее начальному условию
,
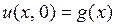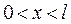
и граничным условиям
, 
, ,
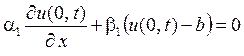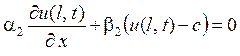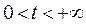где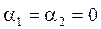 
, 
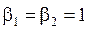для нечётных вариантов; 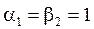, 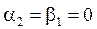для чётных вариантов. Вид функции 
изображён на рисунке.
|
|
|
№ |
|
|
|
|
№ |
|
|
|
|
|
3.1. |
3,0 |
1,1 |
3,5 |
0,06 |
3.2. |
4,0 |
1,2 |
4,0 |
0,16 |
|
3.3. |
5,0 |
1,3 |
4,5 |
0,30 |
3.4. |
1,0 |
1,4 |
5,0 |
0,08 |
|
3.5. |
2,0 |
1,5 |
5,5 |
0,20 |
3.6. |
3,0 |
1,6 |
6,0 |
0,36 |
|
3.7. |
4,0 |
1,7 |
6,5 |
0,56 |
3.8. |
2,0 |
4,0 |
18,0 |
1,20 |
|
3.9. |
1,0 |
1,9 |
7,5 |
0,18 |
3.10. |
2,0 |
2,0 |
8,0 |
0,40 |
|
3.11. |
3,0 |
2,1 |
8,5 |
0,66 |
3.12. |
4,0 |
2,2 |
9,0 |
0,95 |
|
3.13. |
5,0 |
2,3 |
9,5 |
1,30 |
3.14. |
1,0 |
2,4 |
10,0 |
0,28 |
|
3.15. |
2,0 |
2,5 |
10,5 |
0,60 |
3.16. |
3,0 |
2,6 |
11,0 |
0,96 |
|
3.17. |
4,0 |
2,7 |
11,5 |
1,36 |
3.18. |
5,0 |
2,8 |
12,0 |
1,80 |
Задача 4. Найти стационарное распределение температуры в прямоугольной пластинке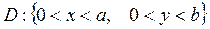 
, если известны значения температуры на границе пластинки:
, 
,
, 
,
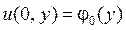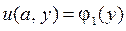
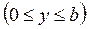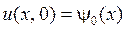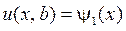
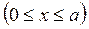причём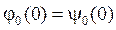 
, 
, 
, 
, 
.
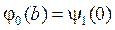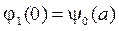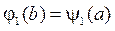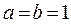4.1.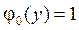 
, 
, 
, 
.
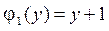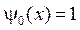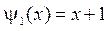4.2. , , ,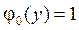 
.
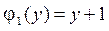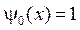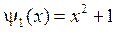4.3.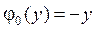 
, 
, 
, 
.
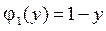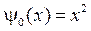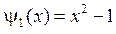4.4.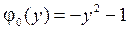 
, 
, 
, 
.
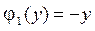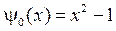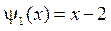4.5.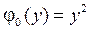 
, 
, , 
.
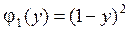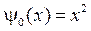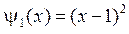4.6.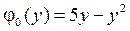 
, 
, 
, 
.
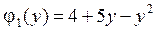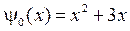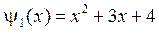4.7.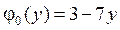 
, 
, 
, 
.
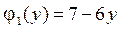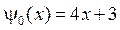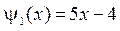4.8. ,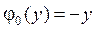 
, 
, .
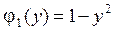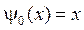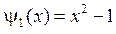4.9.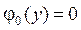 
, 
, 
, 
.
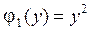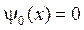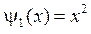4.10. ,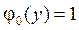 
, , .
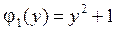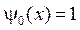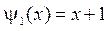4.11. ,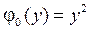 
, 
, .
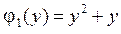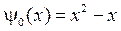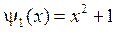4.12.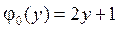 
, 
, , 
.
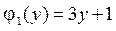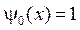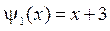4.13. ,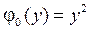 
, 
, 
.
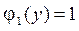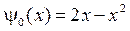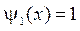4.14. ,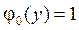 
, 
, 
.
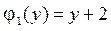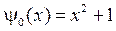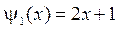4.15.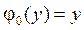 
, , , 
.
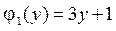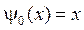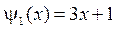4.16. , , ,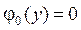 
.
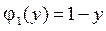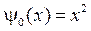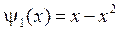4.17.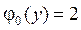 
, 
, 
, 
.
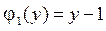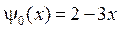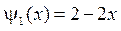4.18.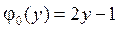 
, 
, 
, .
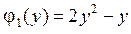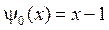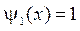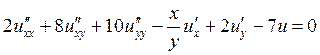МГМИМО