Условия прочности и жёсткости

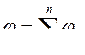, (5.14)

где – угол закручивания i-го участка;

n – число участков.

5.2.3. Напряжение

Подставляя (5.12) в (5.9), получим формулу, определяющую касательные напряжения, действующие в нормальном сечении вала:

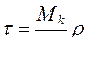. (5.15)

Максимальные значения касательных напряжений, возникающих на контуре сечения, т. е. при 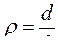(d – диаметр вала), можно записать в виде: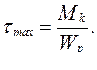

В случае круглого сечения .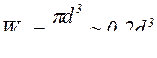

5.2.4. Условия прочности и жёсткости

Условие прочности при кручении записывается как

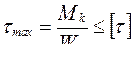, (5.16)

где [τ] – принятое допускаемое значение касательных напряжений для материала вала.

Условие (5.16) прочности при кручении вала позволяет решать следующие основные задачи:

– проектировочный расчёт: по известному значению крутящего момента в сечении и материалу вала ([τ]) подбираются необходимые размеры поперечного сечения для обеспечения безопасности работы по величине полярного момента сопротивления:

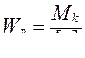, (5.17)

по значению Wр определяют диаметр вала;

– проверочный расчёт: по известному размеру вала и материалу из которого он изготовлен (задано [τ]), проверяется, выдержит ли он заданную нагрузку в виде крутящего момента ; используется выражение (5.16);

– определение допускаемой внешней нагрузки [М] (или установление работоспособности). По известным геометрическим параметрам сечения (Wp – задано) и материалу вала ([τ]) находится допускаемая величина внешней нагрузки:

[М] = [τ] Wp. (5.18)

Выбор величины допускаемого напряжения при кручении [τ] зависит как от свойств материала вала, так и от принятого коэффициента запаса прочности [n].

При расчёте стальных валов в случае статического нагружения можно использовать эмпирическую зависимость [τ] = (0,5 – 0,6) [σ].

Примечание. Большинство валов испытывают при работе переменные по времени нагрузки, они также воспринимают одновременно и изгибные нагрузки, поэтому их нагружения нельзя считать статическими, и в практике машиностроения для стальных валов, в зависимости от материала и условий работы, принимают более низкий диапазон изменения допускаемых напряжений, а именно: [τ] = 20 – 40 МПа.

Произведение GJp называется жёсткостью вала при кручении. Она характеризует способность вала сопротивляться скручиванию. В технике наряду с оценкой прочности валов имеет значение соблюдение условий жёсткости, т. е. условий, исключающих появление при эксплуатации чрезмерных деформаций. Условие жёсткости для валов имеет очевидный вид:

. (5.19)

При проектировочном расчёте:

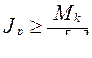. (5.20)

При проверочном расчёте:

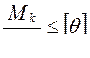. (5.21)

Допускаемый относительный угол закручивания [θ] принимается для разных конструкций валов и различных видов нагрузки в диапазоне 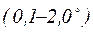или (0,00175–0,035 рад.) на один метр длины вала.

Вопросы для самопроверки

1. Что называется сдвигом?

2. Что называется абсолютным и относительным сдвигом?

3. Как формулируется закон Гука при сдвиге?

4. Как связаны между собой модуль продольной упругости Е и модуль сдвига G?

5. Как производится расчёт на прочность при сдвиге?

6. Какой вид деформации называют кручением?

7. Чему равен крутящий момент в каком-либо сечении вала?

8. Как определяют наибольший крутящий момент?

9. Как определяют напряжение при кручении?

10. Как определяется угол закручивания вала?

11. Чему равна жёсткость стержня (вала) при кручении и что она характеризует?

6. Напряжённое и деформированное состояние в точке

6.1. Напряжённое состояние в точке

Понятие «напряжение в точке» связано как с самой точкой, так и с положением площадки, проведённой через данную точку. Поскольку через точку тела можно провести бесчисленное множество сечений, то в данной точке имеется и бесчисленное множество напряжений, связанных с площадками их действия Совокупность нормальных и касательных напряжений для множества элементарных площадок, проходящих через точку, называется напряжённым состоянием в точке. Сущность метода расчёта на прочность по допускаемым напряжениям состоит в нахождении этих напряжений, определении экстремальных значений и в сравнении их с допускаемым напряжением для материала элемента конструкции.

Вырежем около анализируемой точки D сечения тела элементарный параллелепипед (рис. 28а), оси которого (рис. 28б) ориентированы так же, как и оси х, у, z, по которым раскладывались главный вектор и главный момент внутренних сил в сечении, т. е. грани параллельны координатным плоскостям.

На гранях элементарного параллелепипеда внутренние силы ввиду малости площадок можно считать равномерно распределёнными в пределах каждой грани. По определениям (1.4)–(1.6) внутренние равномерные силы на элементарных гранях считаются напряжениями в точке.

Разложив полное напряжение в точке D по осям координат, получим систему напряжений в точке (у касательных напряжениях первый индекс указывает ось, перпендикулярно которой расположена площадка; второй − ось, параллельно которой действует напряжение σx, σy, σz, τху, τух, τzx, τxz, τyz, τzy). При изменении ориентации параллелепипеда около выбранной точки D (например, поворота) по его граням будет действовать другая система напряжений, значения которых могут быть определены через старые.

Так как мысленно вырезанный из тела параллелепипед, по предположению, находится в равновесии под действием системы напряжений в точке, то суммы проекций всех сил на оси координат и суммы моментов всех сил относительно координатных осей должны быть равны нулю. Из этого следует:

– нормальные напряжения на противоположных гранях равны и противоположно направлены;

– на взаимно перпендикулярных площадках координатные составляющие касательных напряжения равны и направлены либо к смежному ребру, либо от него. Это положение носит название закона парности касательных напряжений.

Среди бесчисленного множества площадок, проходящих через рассматриваемую точку, имеется, по меньшей мере, три взаимно перпендикулярные площадки, на которых отсутствуют касательные напряжения. Такие площадки называются главными. Нормальные напряжения на главных площадках называются главными и обозначаются 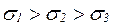с учётом знаков (после определения численных значений).

Если отличны от нуля все три главных напряжения, то такое напряжённое состояние называется трёхосным или объёмным.

Если одно из главных напряжений равно нулю, то такое напряжённое состояние называется двухосным или плоским.

Если равны нулю два главных напряжения, то напряжённое состояние – одноосное или линейное.

Зная напряжённое состояние в любой точке детали, можно оценить прочность самой детали.

6.2. Напряжённое состояние при растяжении (сжатии)

Для того чтобы иметь представление о прочности материала, необходимо знать действующие напряжения не только в плоскости поперечного сечения, но и по любому наклонному сечению.

Рассмотрим стержень, который находится под действием растягивающей силы (рис. 29). Полагаем, что в поперечных сечениях стержня, достаточно удалённых от точек приложения сосредоточенных сил, нормальные напряжения распределяются равномерно и определяются по формуле (2.3):