Условия равновесия термодинамической системы
при T, p=const 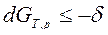 ℒT, p, (25)
ℒT, p, (25)
где ![]() ℒ=
ℒ=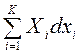 — сумма работ немеханического характера. Для конечного процесса 1-2 эти выражения запишем в виде, умножив левые и правые части уравнений (22)-(25) на минус единицу (-1). Тогда:
— сумма работ немеханического характера. Для конечного процесса 1-2 эти выражения запишем в виде, умножив левые и правые части уравнений (22)-(25) на минус единицу (-1). Тогда:
ℒs,V, (26)
ℒs,p, (27)
ℒT,V, (28)
ℒT,p, (29)
При протекании обратимых процессов работа немеханического характера ℒ максимальна и равна уменьшению соответствующей характеристической функции, т. е.:
ℒs, V max,
ℒs, p max,
(30)
ℒT, V max,
ℒT, p max.
При протекании необратимых процессов с максимальными потерями работоспособности ТС работа немеханического характера равна нулю, т. е.
ℒmin=0. (31)
В общем случае при необратимых процессах часть энергии упорядоченного движения материи диссипирует (рассеивается) в энергию теплового неупорядоченного движения и работа немеханического характера ТС ℒ будет меньше максимальной работы в обратимых процессах.
В термодинамике характеристические функции: U, H, F, G, дифференциалы которых с обратным знаком равны элементарной работе немеханического характера, называют термодинамическими потенциалами:
U – изохорно-изоэнтропийный потенциал,
H – изобарно-изоэнтропийный потенциал,
F – изохорно-изотермический потенциал,
G – изобарно-изотермический потенциал.
Уменьшение термодинамических потенциалов при фиксации двух параметров в обратимых процессах равно максимальной работе ТС.
Таким образом, сумма работ немеханического характера может быть определена через изменения характеристических функций при фиксации двух независимых параметров.
7.4. Условия равновесия термодинамической системы. Термодинамическое сродство
Любая термодинамическая система (ТС) может находиться либо в равновесном, либо в неравновесном состояниях. Общим условием равновесия в механике является равенство нулю суммы работ при малых перемещениях, отвечающих связям системы. Этому условию соответствует экстремум потенциальной энергии. Если это минимум, то при смещении от состояния равновесия расходуется положительная работа (dℒ>0) и состояние равновесия является устойчивым. В термодинамике роль потенциальной энергии выполняют характеристические функции.
Условия термодинамического равновесия для различных сопряжений ТС с окружающей средой с фиксацией двух параметров определяются по поведению характеристических функций, которые позволяют судить о направлении протекания химических реакций и фазовых переходов.
Для простых (dℒ=0), закрытых 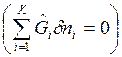 ТС при фиксации двух параметров имеем:
ТС при фиксации двух параметров имеем:
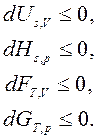 (32)
(32)
Для необратимых процессов:
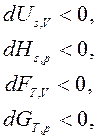 (33)
(33)
т. е. необратимые, неравновесные процессы в простой, закрытой ТС протекают в направлении уменьшения соответствующего термодинамического потенциала. В состоянии равновесия значение соответствующего потенциала достигает минимума, и условия равновесия ТС имеют вид:
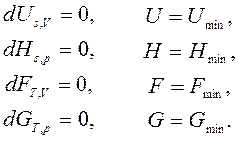 (34)
(34)
При отклонении от состояния равновесия в любую сторону соответствующий термодинамический потенциал возрастает.
Рассмотрим равновесие закрытых ТС, у которых, кроме условий сопряжения с окружающей средой, имеет место воздействие лишь одной силы немеханического характера. Тогда объединенные выражения 1-го и 2-го уравнений термодинамики примут вид:
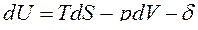 ℒ,
ℒ,
ℒ,
ℒ, (35)
ℒ.
Работу немеханического характера ℒ в (35) будем представлять в виде:
![]() ℒ
ℒ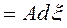 , Дж, (36)
, Дж, (36)
где А – термодинамическое сродство, Дж/моль, x — путь термодинамического процесса, моль.
Термодинамическое сродство вводится соотношением:
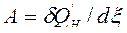 , Дж/моль, (37)
, Дж/моль, (37)
где ![]() — некомпенсируемая теплота, т. е. количество работы, которое диссипировало (рассеялось) в энергию теплового движения частиц на длине пути процесса. Таким образом, термодинамическое сродство – это количество энергии упорядоченного движения частиц (работы), которое диссипировало (рассеялось) на длине пути процесса внутри ТС. При А=0 – процесс обратимый, при А>0 – процесс необратимый. После подстановки выражения (36) для ℒ в уравнения (35) получим:
— некомпенсируемая теплота, т. е. количество работы, которое диссипировало (рассеялось) в энергию теплового движения частиц на длине пути процесса. Таким образом, термодинамическое сродство – это количество энергии упорядоченного движения частиц (работы), которое диссипировало (рассеялось) на длине пути процесса внутри ТС. При А=0 – процесс обратимый, при А>0 – процесс необратимый. После подстановки выражения (36) для ℒ в уравнения (35) получим:
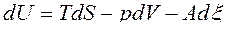 ,
,
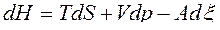 ,
,
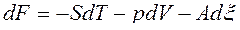 , (38)
, (38)
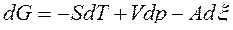 .
.
Таким образом, U=U(S,V,x), H=H(S,p, x), F=F(T,V,x), G=G(T,p, x) и при фиксации двух первых параметров в уравнениях (38) будем иметь:
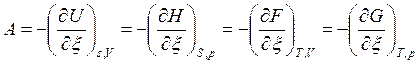 . (39)
. (39)
Так, потенциал Гиббса при фиксации значений Т и р из (38) равен:
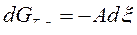 , (40)
, (40)
т. е. 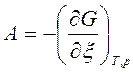 .
.
Следовательно, термодинамическое сродство определяется через частные производные характеристических функций по пути процесса ![]() .
.
Примером термодинамического сродства является химическое сродство. В этом случае величина пути процесса называется пробегом химической реакции.
При стремлении ТС к состоянию равновесия потенциал Гиббса стремится к минимуму своего значения (GT,p ®GT,p min) при фиксированных значениях Т и р , которое достигается при равновесном значении ![]() (при этом величина термодинамического сродства А=0), как это видно из приведенного рисунка:
(при этом величина термодинамического сродства А=0), как это видно из приведенного рисунка:
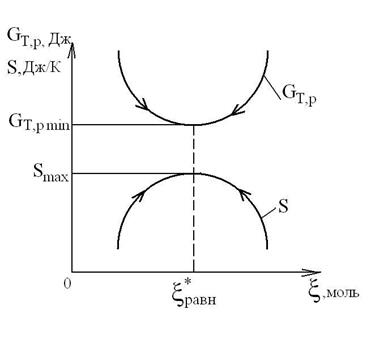
Равновесное состояние ТС можно охарактеризовать также по изменению энтропии. При необратимых, неравновесных процессах внутри адиабатной, закрытой ТС изменение энтропии dS=dSin>0, т. е. энтропия растет и достигает максимума в состоянии равновесия: dS=0, S=Smax . При раскачивании ТС относительно состояния равновесия энтропия будет уменьшаться, а термодинамические потенциалы увеличиваться.
7.5. Связь между изобарной и изохорной теплоемкостями в общем виде
Функция состояния ТС – энтропия может быть представлена в виде функциональной связи S=S(T,V). Дифференциал энтропии – полный дифференциал, т. е.
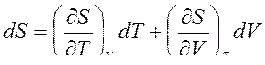 . (1)
. (1)


