| Вращение твердого тела вокруг неподвижной оси

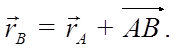При поступательном движении твердого тела траектории, скорости и ускорения всех точек тела одинаковы (рис. 22).

Рис. 22

Вектор АВ является всегда постоянным по модулю, а при поступательном движении не изменяется и по направлению.

При сдвиге на АВ траектории точек совпадут.

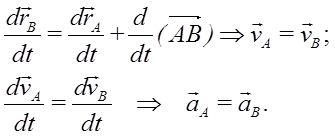
Движение твердого тела, для которого векторы скоростей точек равны только в один момент времени, а не все время, называется мгновенным поступательным движением.

Для мгновенного поступательного движения ускорения точек в общем случае не являются одинаковыми.

2.8. Вращение твердого тела вокруг неподвижной оси

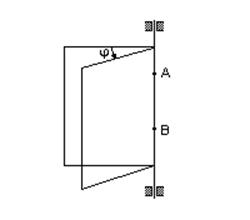Вращательным движением твердого тела вокруг неподвижной оси называется такое его движение, при котором две точки тела (или его продолжения) остаются неподвижными в течение всего времени движения (рис.23).

Прямая, соединяющая эти точки, называется осью вращения.

Рис. 23

Положение тела относительно выбранной системы отсчета полностью и однозначно определяется в любой момент времени, если задано уравнение , то есть у тела одна степень свободы.

Угловая скорость, 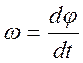Угловое ускорение

2.9. Плоское движение твердого тела

Плоским движением твердого тела называют такое его движение, при котором каждая его точка все время движется в одной и той же неподвижной плоскости. Часто это движение называют плоскопараллельным, так как плоскости, в которых движутся отдельные точки, параллельны между собой.

Траектории точек тела при плоском движении являются плоскими кривыми. Такой случай движения часто реализуется в технике при движении механизмов и машин. Вращательное движение твердого тела вокруг неподвижной оси является частным случаем плоского движения.

Для изучения плоского движения твердого тела достаточно рассмотреть движение плоской фигуры в ее плоскости, параллельной неподвижной плоскости П0. Для задания положения плоской фигуры на плоскости относительно координат Oxy достаточно задать на 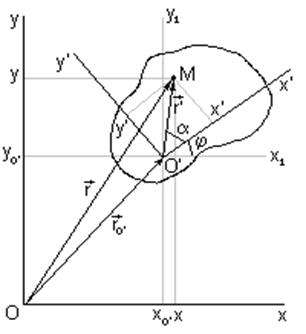этой плоскости положение отрезка О’M, скрепленного с фигурой (рис. 24).

Скрепим с твердым телом подвижную систему осей O’x’y’

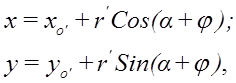Тогда для координат (x, y) точки М будем иметь:

где , α − постоянный угол между O’M и осью O’x’.

Рис. 24

Разложение плоского движения твердого тела на поступательное и вращательное

Любое движение твердого тела, в том числе движение плоской фигуры в ее плоскости, бесчисленным множеством способов можно разложить на два движения, одно из которых поступательное (переносное), а другое – вращательное (относительное) (Рис.25).

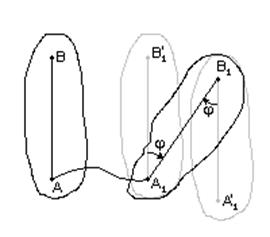Пусть тело в своем движении переходит из одного состояния в другое. Мы можем представить это движение двумя способами:

1) тело совершает поступательное перемещение, когда точка А совмещается с А1, потом доворачиваем тело вокруг точки А1,

2) тело совершает поступательное перемещение, когда точка В совмещается с В1,потом доворачиваем тело вокруг точки В1.

Рис. 25 Точки А1 и В1, вокруг которых мы дово-

рачиваем фигуру, называют полюсами.

Нетрудно заметить, что поворот фигуры всегда будет одним и тем же (на угол φ), независимо от выбора полюса. Поступательное перемещение зависит от выбора точки – полюса.

2.10. Скорость точек тела при плоском движении

Мгновенный центр скоростей

Выбираем точку А за полюс – начало отсчета подвижной системы координат, движущейся только поступательно, относительное движение будет "чистым" вращением (рис. 26).

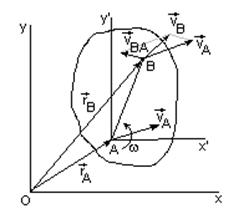Системы осей параллельны: Аx’ || Ox ; Ay’ || Oy.

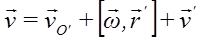Из уравнений для сложного движения точки

имеем:

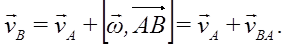
Рис. 26

Скорость какой-либо точки фигуры при ее плоском движении равна векторной сумме скорости полюса (переносной) и относительной скорости этой точки от вращения фигуры вокруг полюса. Эта формула выражает зависимость между скоростями двух любых точек тела при плоском движении в любой момент времени.

В каждый момент времени при плоском движении фигуры, если ω≠0, имеется единственная точка этой фигуры (или ее продолжения), скорость которой равна нулю. Эту точку называют мгновенным центром скоростей.

Способы нахождения мгновенного центра скоростей.

Мгновенный центр скоростей можно найти либо из механических условий задачи (точка касания колеса, катящегося без проскальзывания), либо по скоростям точек плоской фигуры.

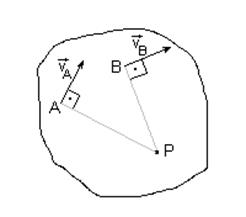
Если известны скорости двух точек плоской фигуры (рис. 27), мгновенный центр скоростей находится на пересечении перпендикуляров к скоростям этих точек.

Рис. 27

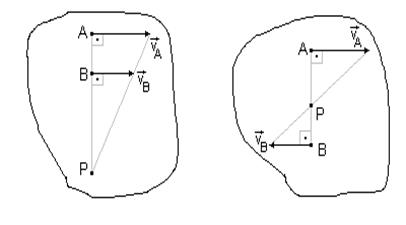В том случае (Рис. 28), когда точки лежат на общем перпендикуляре к скоростям этих точек и скорости точек параллельны, концы векторов скоростей точек лежат на одной прямой, проведенной через мгновенный центр ско-ростей, так как скорости то-чек пропорциональны расстоя — Рис. 28

ниям от этих точек до центра скоростей.

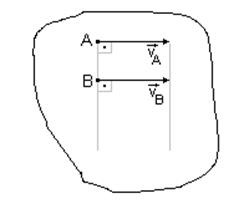Если скорости двух точек, расположенных на общем перпендикуляре к этим скоростям, еще и равны (Рис. 29), мгновенный центр скоростей находится на бесконечности и мы имеем мгновенное поступательное движение плоской фигуры, при котором скорости всех точек фигуры одинаковы по модулю и направлению (w=0).

При этом мгновенном поступа-тельном движении только скорости точек одинаковы, а их ускорения в общем случае различны.

Рис. 29

2.11. Ускорения точек при плоском движении тела

Мгновенный центр ускорений

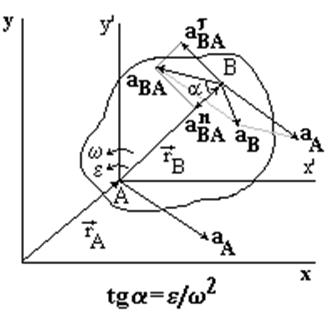За переносное движение тела примем поступательное движение, за относительное движение – вращение тела вокруг полюса А (рис. 30).

Полюс А движется с ускорением aA и тело вращается вокруг полюса с угловой скоростью ω и угловым ускорением ε. Из формул для сложного движения точки имеем:

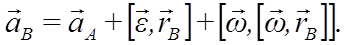
Рис. 30

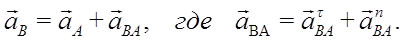Эту формулу можно представить в виде

Точка В получает ускорение aBA вследствие вращения вокруг полюса А, компоненты этого ускорения определяются так:

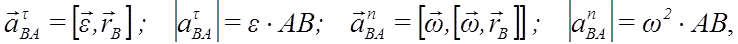
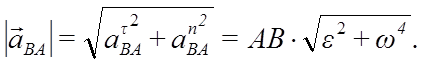
отсюда

Мгновенный центр ускорений. В каждый момент движения плоской фигуры в своей плоскости, если ω и ε не равны нулю одновременно, имеется единственная точка этой фигуры, ускорение которой равно нулю. Эту точку называют мгновенным центром ускорений, мы будем ее обозначать Q.

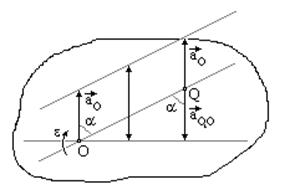Пусть нам известны по модулю и направлению ускорение какой-либо точки плоской фигуры (точка О), угловая скорость и угловое ускорение ε этой фигуры (рис. 31).