Задача на электромагнитную индукцию
Произведем вычисления: 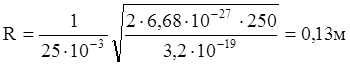
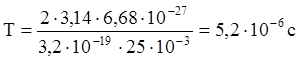
Ответ: 0,13 м; 5,2·10-6 с.
10) Задача на электромагнитную индукцию.
Катушка сопротивлением 100 Ом, состоящая из 1000 витков, внесена в однородное магнитное поле, так что линии магнитной индукции параллельны оси катушки. Площадь поперечного сечения катушки равна 5 см2. В течение некоторого времени индукция магнитного поля уменьшилась с 0,09 до 0,04 Тл. Какой заряд индуцирован в проводнике за это время?
Запишем краткое условие задачи.
|
Решение: При изменении магнитного потока, пронизывающего катушку в ней возникает индукционный ток силой, по закону Ома равный: |
 Дано: СИ
Дано: СИ
R=100 Ом
N=1000
S=5см2 =5·10-4м2
B1=0,09Тл
B2=0,04Тл
 q-?
q-?
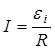 , где
, где ![]() — ЭДС индукции. По определению сила тока
— ЭДС индукции. По определению сила тока 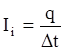 , где
, где ![]() — время протекания заряда через поперечное сечение провода.
— время протекания заряда через поперечное сечение провода.
Приравниваем: 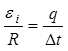 . Отсюда
. Отсюда 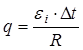 .
.
По закону Фарадея ЭДС индукции, возникающая в катушке содержащей N витков: 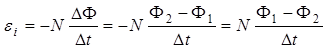 ,
,
где 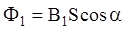 ,
, 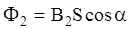 .
.
Угол α между нормалью к плоскости контура и линией магнитной индукции по условию задачи равен нулю, поэтому 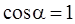 .
.
С учетом этого 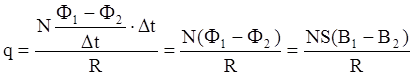 .
.
Проведем проверку размерности:
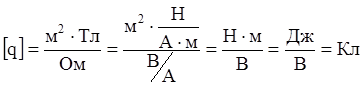
Произведем вычисления: 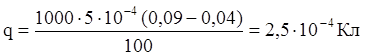 .
.
Ответ: 2,5·10-4 Кл
11) Задача на идеальный колебательный контур.
Колебательный контур состоит из конденсатора емкостью С=5 мкФ и катушки индуктивности L = 0,2 Гн. Определить максимальную силу тока I0 в контуре, если максимальная разность потенциалов на обкладках конденсатора U0 = 90 В. Активным сопротивлением проводов в контуре пренебречь.
Запишем краткое условие задачи.
|
Решение: Воспользуемся законом сохранения энергии для идеального колебательного контура:
|
 Дано: СИ
Дано: СИ
L=0,2 Гн
С=5 мкФ =5·10-6Ф
U0= 90В

I0 -?
Полная энергия контура равна энергии конденсатора при максимальном значении U: 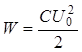 .
.
Сила тока достигает максимального значения в момент разрядки конденсатора, при этом 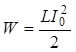 .
.
Следовательно, 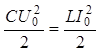 .
.
Откуда: 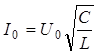 .
.
Произведем вычисления: 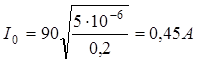 .
.
Ответ: 0,45 А
12) Задача на формулу Томсона.
В колебательный контур включен конденсатор емкостью С=0,2 мкФ. Какую индуктивность L нужно включить в контур, чтобы получить в нам электромагнитные колебания частоты υ = 400Гц?
Запишем краткое условие задачи.
|
Решение: Воспользуемся формулой Томсона: Циклическая частота равна ω = 2πυ |
 Дано: СИ
Дано: СИ
С=0,2 мкФ =0,2·10-6Ф
υ= 400Гц

L -?
Следовательно, 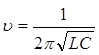 .
.
Откуда 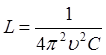
Произведем вычисления: 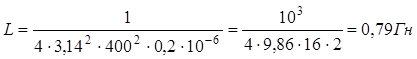 .
.
Ответ: 0,79 Гн.
Задачи для контрольной работы
|
Варианты. |
Номера задач |
|
1 2 3 4 5 6 7 8 9 0 |
1 11 21 31 41 51 61 71 81 91 3 12 22 32 42 52 62 72 82 92 3 13 23 33 43 53 63 73 83 93 4 14 24 34 44 54 64 74 84 94 5 15 25 35 45 55 65 75 85 95 6 16 26 36 46 56 66 76 86 96 7 17 27 37 47 57 67 77 87 97 8 18 28 38 48 58 68 78 88 98 9 19 29 39 49 59 69 79 89 99 10 20 30 40 50 60 70 80 90 100 |
1. Электрическое поле создано двумя точечными зарядами 2·10-7 Кл и — 2·10-7 Кл. Расстояние между зарядами 50 см. Определить напряженность электрического поля в точке, находящейся на расстоянии 30 см от одного заряда и 40 см от другого заряда.
2. Поле создано бесконечной плоскостью с поверхностной плотностью заряда 4·10-5 Кл/м2, к которой подвешен на нити шарик массой 1 г и зарядом 10-9 Кл. Определить угол, образованный нитью и плоскостью.
3. Два точечных заряда 1 Кл и – 4 Кл расположены в 12 м друг от друга. На каком расстоянии от второго заряда напряженность электрического поля равна нулю?
4. Четыре одинаковых положительных точечных заряда q = 10мкКл закреплены в вершинах квадрата со стороной 1 м. Найти силу, действующую со стороны трех зарядов на четвертый.
5. Частица массой 2 мг и зарядом 5·10-6 Кл находится в однородном поле напряженностью 200 кВ/м. Какой путь пройдет частица за 4 мс, если ее начальная скорость равна нулю?
6. Два точечных заряда 1 мкКл и – 4 мкКл расположены в воздухе на расстоянии 20 см друг от друга. Определить напряженность электрического поля в точке, расположенной на расстоянии 12 см от первого заряда и 16 см от второго.
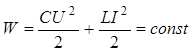
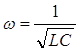 .
.

