Задачи об относительности промежутков времени
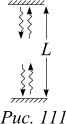 Пусть на быстроходной ракете отсчет времени ведется с помощью световых часов. Напротив друг друга установлены два идеальных зеркала, полностью отражающих падающий свет. Расстояние между зеркалами L. Вспышка света, отражаясь, мечется между зеркалами. Свет распространяется перпендикулярно направлению движения ракеты. Вспышка играет роль маятника в обычных механических часах. Для наблюдателя, летящего вместе с часами в ракете (в системе отсчета этого наблюдателя часы покоятся), период колебаний светового “маятника” 2t равен 2L/c. Промежуток времени между двумя какими-либо событиями A и B, измеренный с помощью этих часов, будет равен числу периодов колебаний, успевших произойти за измеряемое время.
Пусть на быстроходной ракете отсчет времени ведется с помощью световых часов. Напротив друг друга установлены два идеальных зеркала, полностью отражающих падающий свет. Расстояние между зеркалами L. Вспышка света, отражаясь, мечется между зеркалами. Свет распространяется перпендикулярно направлению движения ракеты. Вспышка играет роль маятника в обычных механических часах. Для наблюдателя, летящего вместе с часами в ракете (в системе отсчета этого наблюдателя часы покоятся), период колебаний светового “маятника” 2t равен 2L/c. Промежуток времени между двумя какими-либо событиями A и B, измеренный с помощью этих часов, будет равен числу периодов колебаний, успевших произойти за измеряемое время.
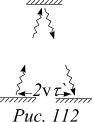 Пусть теперь с помощью тех же самых часов (расположенных на ракете) промежуток времени между этими же событиями измеряет наблюдатель, находящийся на Земле. Скорость ракеты относительно Земли равна v. Для наблюдателя с Земли свет, отражаясь от зеркал, не колеблется на месте. Он движется зигзагом. Предположим, что расстояние между зеркалами с точки зрения земного наблюдателя то же самое, что и с точки зрения наблюдателя, находящегося в ракете. От зеркала до зеркала свету приходится проходить большее расстояние, равное
Пусть теперь с помощью тех же самых часов (расположенных на ракете) промежуток времени между этими же событиями измеряет наблюдатель, находящийся на Земле. Скорость ракеты относительно Земли равна v. Для наблюдателя с Земли свет, отражаясь от зеркал, не колеблется на месте. Он движется зигзагом. Предположим, что расстояние между зеркалами с точки зрения земного наблюдателя то же самое, что и с точки зрения наблюдателя, находящегося в ракете. От зеркала до зеркала свету приходится проходить большее расстояние, равное 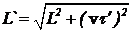 , где t` — полупериод колебаний часов, измеренный земными часами. Ясно, что 2t`c=2L`. Учитывая это, получаем уравнение для t`:
, где t` — полупериод колебаний часов, измеренный земными часами. Ясно, что 2t`c=2L`. Учитывая это, получаем уравнение для t`:
c2t`2=L2+(vt`)2. (1)
Решим это уравнение относительно t`. Получим
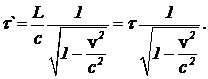 (2)
(2)
С точки зрения земного наблюдателя время одного ”тика” часов на ракете больше времени одного ”тика” покоящихся часов, т. е. часы с его точки зрения на ракете идут медленнее. Точно так же время между двумя событиями A и B для наблюдателя с Земли будет большим, поскольку отмеченное число колебаний часов длится большее время. Время, отмечаемое часами, покоящимися в данной системе отсчета, называется собственным временем. Собственное время между двумя событиями является самым меньшим среди всех времен, измеряемых в различных системах отсчета.
Приведенные выше выводы не связаны со специфическим устройством движущихся часов. Они относятся не к часам, а к течению времени. Все процессы, включая биологические, с точки зрения земного наблюдателя, на ракете протекают медленнее, чем те же процессы на Земле.
Рассмотрим пример природного процесса, в котором проявляется относительность промежутков времени. На высоте около L=12 км в результате облучения атмосферы высокоэнергичными космическими частицами (протонами) происходит интенсивное рождение новых частиц — мюонов (m—). Среднее время жизни tm покоящегося мюона равно 2,2 мкс (за среднее время жизни первоначальное число мюонов уменьшается в e раз). Родившиеся в верхних слоях атмосферы мюоны со скоростью, близкой к скорости света, летят к Земле. Ясно, что за среднее время жизни даже при скорости света мюоны могут пролететь расстояние, равное только b=tmс= 2,2×10-6×3×108=660 м. На этом расстоянии от места рождения интенсивность потока мюонов из-за распадов уменьшается в e раз. На следующих 660 метрах произойдет уменьшение интенсивности еще в e раз. В момент прилета к поверхности Земли интенсивность потока должна была бы уменьшиться в 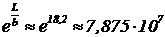 раз. Однако эксперименты на стратостатах по измерению потока мюонов в верхних слоях атмосферы показали, что интенсивность падает не в 80 миллионов раз, а только в небольшое число раз. Объяснение этому дает представление о замедлении всех процессов в движущейся системе отсчета. Можно представить себе, что мюон внутри себя имеет какую-то адскую машину с часами, которая запускает механизм распада. По собственному времени запуск должен происходить через 2,2 мкс после рождения. Однако для земного наблюдателя, относительно которого часы мюона движутся со скоростью, близкой к скорости света, их ход сильно замедлен, и по времени наблюдателя запуск происходит гораздо позднее, чем “положено”.
раз. Однако эксперименты на стратостатах по измерению потока мюонов в верхних слоях атмосферы показали, что интенсивность падает не в 80 миллионов раз, а только в небольшое число раз. Объяснение этому дает представление о замедлении всех процессов в движущейся системе отсчета. Можно представить себе, что мюон внутри себя имеет какую-то адскую машину с часами, которая запускает механизм распада. По собственному времени запуск должен происходить через 2,2 мкс после рождения. Однако для земного наблюдателя, относительно которого часы мюона движутся со скоростью, близкой к скорости света, их ход сильно замедлен, и по времени наблюдателя запуск происходит гораздо позднее, чем “положено”.
2.2 Задачи об относительности промежутков времени
Задача 1. Определить скорость мюонов, родившихся на высоте 13 200 м, если их поток на поверхности Земли в e раз меньше потока на высоте рождения.
Задача 2. Какое расстояние мог бы пролететь мюон до распада, если бы отличие его скорости от скорости света составляло бы всего 10-6×c?
2.3 Относительность длин
С точки зрения преобразований Галилея, переход из одной инерциальной системы отсчета в другую представляет собой плоскопараллельный перенос, в результате которого расстояние между двумя заданными точками не изменяется. Неизменность скорости света требует, чтобы длины при переходе из одной инерциальной системы отсчета в другую изменялись (см. рассмотрение взаимодействия электрона с проводом с током из занятия 1.5.1).
Рассмотрим создание эталона длины, полагая, что эталон измерения времени уже есть (световые часы, описанные в разделе 2.1). Выясним, как эталон длины, созданный в одной системе отсчета и ориентированный вдоль направления движения системы, выглядит в другой системе отсчета, относительно которой первая движется со скоростью v. Поскольку нам уже известно, как преобразуются промежутки времени при переходе из одной системы отсчета в другую, при создании эталона будем опираться на процедуру измерения времени.
Вернемся в ракету, на которой раньше были световые часы (раздел 2.1.2). Допустим, в ракете подобрали стержень, подходящий для использования в качестве эталона. Этому эталону надо приписать какую-то величину длины. Данную процедуру выполнили следующим образом. На одном конце укрепили импульсный источник света и приемник, на другом — зеркало. После запуска источника свет проходит расстояние до зеркала, возвращается обратно и принимается приемником. Регистрируется время tо между посылкой и приемом светового сигнала. И величину 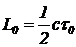 (3) можно считать длиной эталона. Ясно, что в системе отсчета, связанной с ракетой, при любой ориентации стержня измерения будут давать одно и то же значение L0.
(3) можно считать длиной эталона. Ясно, что в системе отсчета, связанной с ракетой, при любой ориентации стержня измерения будут давать одно и то же значение L0.
Рассмотрим теперь те же самые измерения с точки зрения земного наблюдателя. Ранее мы предположили, что в перпендикулярном направлении движению ракеты изменения длин не происходит. Пусть теперь стержень ориентирован параллельно направлению движения ракеты. Обозначим за L` длину стержня, фиксируемую наблюдателем с Земли. Скорость ракеты относительно Земли равна v. Наблюдатель, находящийся на Земле, увидит, что после вспышки зеркало будет удаляться от источника, и свету надо будет пройти расстояние большее, чем L`. Если промежуток времени между отправкой светового сигнала и отражением от зеркала равен t1, то справедливо уравнение
ct1=L`+vt1. (4)
Откуда
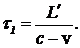 (5)
(5)
Аналогично, для времени t2 — прохождения света от зеркала к приемнику — найдем
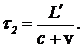 (6)
(6)
Таким образом, промежуток времени t` между отправлением и приемом светового сигнала, с точки зрения земного наблюдателя, равен
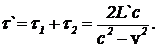 (7)
(7)
С другой стороны, нам уже известно, что время t` между событиями — отправление и прием светового сигнала — в системе отсчета, связанной с Землей выражается через собственное время ракеты t0 соотношением  (8) После подстановки выражения (8) в уравнение (7) получим уравнение, связывающее длину стержня, измеренного в ракете, с длиной, измеренной земным наблюдателем:
(8) После подстановки выражения (8) в уравнение (7) получим уравнение, связывающее длину стержня, измеренного в ракете, с длиной, измеренной земным наблюдателем: 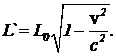 (9)
(9)
Итак, с точки зрения земного наблюдателя, длина стержня в направлении движения сокращается в 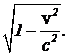 раз по сравнению с длиной в системе отсчета, связанной с ракетой.
раз по сравнению с длиной в системе отсчета, связанной с ракетой.
3. Решение задач
Задача 3. Рассмотрите стержень, ориентированный перпендикулярно направлению движения ракеты. Повторите изложенные выше рассуждения и покажите, что длина таким образом ориентированного стержня в системе отсчета, связанной с землей, та же, что и в системе отсчета, связанной с ракетой.
Задача 4. Принцип относительности говорит, что все инерциальные системы отсчета совершенно равноправны. Это означает, что регистрация мюонов, родившихся в верхних слоях атмосферы, детекторами на поверхности Земли должна так же хорошо объясняться с точки зрения наблюдателя, летящего вместе с мюонами, как и с точки зрения земного наблюдателя. Встаньте на эту “точку зрения мюона” и объясните факт регистрации.


