Задачи по квантовой физике

Задачи для самостоятельного решения. Квантовая физика.

Таблица вариантов

1.1  Модель абсолютно черного тела с выходным отверстием диаметром 0,5 см за 1 минуту излучает 267 Дж. Какова температура модели?

1.2  Одну треть поверхности нагретого тела охладили на 200 К, а у остальной части поверхности температуру повысили на 47,3 К. Как изменилась мощность излучения тела, если первоначальная температура тела была 500 К?

1.3  В течение первых трех минут измерения температура поверхности тела сохраняется 800 К, затем одна половина поверхности тела охлаждается на 100 К, другая нагревается на 200 К, и вновь измеряется мощность в течение двух минут. Найти относительное изменение мощности излучения

1.4  Температура тела в течение часа была равна 500 К. Затем её повысили в два раза, и в течение следующих 30 мин. она оста­валась неизменной. Как изменилась излучаемая телом энергия?

1.5  Найти относительное смещение длины волны, на которую приходится максимум излучательной способности абсолютно чёрного тела, при понижении температуры тела в 1,3 раза.

1.6  При изменении температуры тела длина волны, на которую приходится максимум излучательной способности абсолютно чёрного тела, увеличилась на 20 %. Как изменилась температура тела?

1.7  Длина волны излучения абсолютно чёрного тела, на которую приходится максимум излучательной способности, увеличилась на 20 % за счёт изменения температуры. Как изменилась при этом интегральная излучательная способность и максимальная излучательная способность тела?

1.8  Найти температуру вольфрамовой нити накала электрической лампочки длиной 10 см и диаметром 0,3 мм, если при подключении её к напряжению 12 В по ней проходит ток силой 0,5А. Коэффициент серости вольфрама принять равным 0,25.

1.9  Интегральная излучательная способность обшивки сверхзвукового самолёта при его полёте со скоростью, приближающейся к утроенной скорости звука в воздухе, на высоте более 10 км составляет 0,3 Вт/см2. Какова при этом минимальная температура обшивки самолёта?

1.10  Длина волны, на которую приходится максимум излучательной способности абсолютно чёрного тела, сменилась в сторону увеличения от λ1 до λ2. Найти изменение температуры тела.

1.11  При нагревании абсолютно чёрного тела длина волны, на которую приходится максимум излучательной способности, изменилась от 0,552 до 0,400 мкм. Как изменилась при этом температура тела? Во сколько раз изменилась при этом максимальная излучательная способность тела?

1.12  Определить массу, теряемую Солнцем ежегодно за счёт излучения энергии, принимая Солнце за абсолютно чёрное тело с температурой поверхности 5800 К. Найти, какую часть своей массы теряет Солнце ежегодно? Оценить, на сколько лет хватит массы Солнца, считая мощность его излучения постоянной. Радиус Солнца 6,95 ·108 м, масса 1,97 · 1030 кг.

1.13  Определить, какова мощность излучения абсолютно чёрного тела в виде шарика радиусом 0,3 см при температуре 800 К в узком интервале длин волн от 0,95 до 1,05 длины волны, на которую приходится максимум излучательной способности шарика.

1.14  При взрыве атомной бомбы длина волны, соответствующая максимальной излучательной способности, приходится на область рентгеновских лучей с длиной волны 2,9 · 1010 м. Определить температуру взрыва и мощность излучения с единицы поверхности.

1.15  20-Ваттная лампочка излучает электромагнитные волны длиной 1200 нм. Найти число фотонов, испускаемых лампочкой за 0,5 мин.

1.16  Определить длину волны излучения, квант которого имеет такую же энергию, что и электрон, прошедший ускоряющую разность потенциалов 5 В.

1.17  Лазер мощностью 2 мВт генерирует монохроматическое излучение длиной волны 0,63 мкм. Определить массу фотона и время, за которое лазер испускает фотоны с суммарной массой, равной массе покоя нейтрона.

1.18  Какова должна быть температура молекулы одноатомиого идеального газа, чтобы её энергия была равна энергии фотона с длиной волны 0,55 мкм?

1.19  В каких пределах должна измениться температура молекулы двухатомного идеального газа, чтобы её энергия соответствовала фотонам видимой области спектра?

1.20  Кинетическая энергия двухатомной молекулы идеального газа при температуре 5000 К равна энергии фотона. Чему равны частота и длина волны такого фотона?

1.21  Источник света мощностью 100 Вт испускает 5 ·1020 фотонов за 1 с. Найти длину волны излучения.

1.22  Излучение состоит из фотонов с энергией 5 · 10-19 Дж. Найти длину волны и частоту этого излучения в воде. Показатель преломления воды 1,33.

1.23  Скорость распространения фиолетовых лучей с частотой 7,5 ·1014 Гц в воде 2,33 · 108 м/с. На сколько изменится частота и длина волны этих лучей при переходе из воды в вакуум?

1.24  С какой скоростью должен двигаться электрон, чтобы его кинетическая энергия была равна энергии фотона с длиной волны 5,2-10-7 м?

1.25  Найти энергию, импульс и массу фотонов видимого света (λ1 = 0,5 мкм) и рентгеновского излучения (λ2 = 0,025 нм).

1.26  Какое количество фотонов с длиной волны 0,6 мкм в параллельном пучке будет иметь суммарный импульс, равный среднему импульсу атома гелия при температуре 300 К?

1.27  Определить энергию, импульс и массу фотона, длина волны которого соответствует γ — излучению с длиной волны 0,1 нм.

1.28  Вычислить частоту и длину волны фотона, энергия которого равна энергии покоя электрона.

1.29  Импульс излучения, состоящий из 5·104 квантов света с длиной волны 0,3 мкм, падает на фоточувствительную поверхность, у которой спектральная чувствительность для данной длины волны равна 4,5 мА/Вт. Найти количество фотоэлектронов, освобождаемых таким импульсом света.

1.30  Электрон выбивается из сурьмяно-цезиевого фотокатода. "Красная" граница фотоэффекта соответствует длине волны 5,77 · 10-7 м. Вычислить минимальное значение энергии кванта, необходимое для освобождения фотоэлектронов из данного покрытия фотокатода.

1.31  "Красная" граница фотоэффекта для сурьмяно-цезиевого фотокатода равна 5,77 · 10-7 м. Определить максимальную скорость фотоэлектронов при облучении фотокатода фиолетовыми лучами с длиной волны 4 · 10-7 м.

1.32  Работа выхода электронов с поверхности цезия равна 1,9 эВ. С какой максимальной скоростью вылетают электроны из цезия при освещении его желтым светом длиной волны 0,59 мкм?

1.33  Фотокатод освещается светом длиной волны 0,76 мкм. Определить максимальную скорость фотоэлектронов, если "красная" граница фотоэффекта равна 1,75 мкм.

1.34  Найти число квантов, испускаемых лампочкой мощностью 58 Вт за 1 с, падающих на фотокатод с работой выхода 1,2 эВ, если задерживающий потенциал равен 1,2 В.

1.35  Найти количество фотоэлектронов, выбиваемых с поверхности фотокатода световым потоком с числом квантов 4 · 105 и длиной волны 0,41 мкм. Спектральная чувствительность фотокатода на данной длине волны равна 3,3 мА/Вт.

1.36  Во сколько раз кинетическая энергия фотоэлектронов больше работы выхода электронов из катода с "красной" границей 0,8 · 10-7 м при падении на него света длиной волны 0,4 · 10-7 м?

1.37  "Красная" граница фотоэффекта равна 1,3 длины волны падающего света, и задерживающий потенциал составляет 2 В. Определить работу выхода электронов из вещества фотокатода, а также частоту и длину волны используемого света.

1.38  При освещении двух фотокатодов одним и тем же светом длиной волны 4 · 10-7 м задерживающие потенциалы оказались равными 2,5 и 3 В. Найти отношение работ выхода фотоэлектронов из веществ катодов.

1.39  При освещении фотокатода светом с длинами волн, соответствующими границам видимого спектра, задерживающая разность потенциалов изменилась от 0,63 до 2,1 В. Какое значение постоянной Планка получается по этим данным?

1.40  На частоту света 5 · 1015 Гц приходится 8 % энергии, излу­чаемой лампочкой мощностью 100 Вт. Какая часть энергии идёт на работу выхода электронов из катода, работающего на частоте 5·1015 Гц и освещаемого этой лампочкой, если вели­чина энергии задерживающего потенциала составляет 1/2 рабо­ты выхода? Сколько квантов света падает на фотокатод за 5 с?

1.41  При освещении поверхности фотокатода светом с длинами волн 2,79 · 10-7 и 2,45 · 10-7 м задерживающие потенциалы соответственно равны 0,66 и 1,28 В. Определить значение постоянной Планка.

1.42  Какая доля энергии фотона расходуется на работу выхода электрона с поверхности сурьмя но-цезиевого фотокатода, если "красная" граница фотоэффекта соответствует длине волны.3,07 · 10-7 м, а кинетическая энергия электрона равна 1 эВ?

1.43  На какой максимальной длине волны работает дальномер, если при падении света λ = 4,5 · 10-7 м фототок исчезает при задерживающем потенциале 1 В? Найти работу выхода электронов из фотокатода дальномера.

1.44  В оптическом лазерном дальномере приемником излучения является фотоэлектронный умножитель с работой выхода фотокатода 2 эВ или лавинопролетный диод с работой выхода 0,3 эВ. В каких областях спектра работает дальномер?

1.45  На фотоэлемент с оксидно-цезиевым катодом падают инфракрасные лучи с длиной волны 1 мкм. Определить максимальную кинетическую энергию фотоэлектронов, если "красная" граница фотоэффекта равна 1,2 мкм.

1.46  Какой длины волны свет следует направить на поверхность цезия, чтобы максимальная скорость фотоэлектронов была 2·106 м/с? "Красная" граница фотоэффекта для цезия равна 690 нм.

1.47  Какова максимальная скорость электронов, вырванных с поверхности пластины при облучении ее светом с длиной волны 100 нм? Работа выхода электронов из пластины равна 8 · 10-19 Дж.

1.48  Какой длины волны свет следует направить на поверхность, металлической пластины, чтобы максимальная, скорость фотоэлектронов была равна. 3600 км/с? Рабата выхода электронов из освещаемого металла равна 6,3 эВ.

1.49  Для определения постоянной Планка фотокатод освещает светом различных частот и измеряет задерживающую разность потенциалов. В ходе эксперимента получены следующие данные: при использовании света 0,75 · 1015 Гц и 0,44 · 1015 Гц задерживающие потенциалы соответственно 1,60 и 0,32 В. Рассчитать значение постоянной Планка и найти работу выхода электронов из используемого фотокатода.

1.50  При увеличении длины волны 0,2 мкм света, падающего на фотокатод, на 0,1 мкм задерживающая разность потенциалов 3,3 В изменилась в 3 раза. Оценить погрешность в определении постоянной Планка в данном опыте по сравнению с теоретическим.

1.51  Кальциевый фотокатод, имеющий работу выхода 2,76 эВ, осве­щается светом с длиной волны 3 · 10-7 м. Вылетающие из катода электроны попадают в однородное магнитное поле с индукцией 0,6 мТл перпендикулярно линиям индукции этого поля. Чему равен максимальный радиус окружности, по которой движется электрон? Найти периоды обращения электронов в поле.

1.52  Электроны, вылетающие из фотокатода с работой выхода 3 эВ, освещаемого светом с длиной волны 0,25 мкм, попадают в однородное магнитное поле с индукцией 0,5 мТл. Какова траектория движения электронов, если они влетают в поле под углом 45° к направлению вектора индукции?

1.53  Вылетающие из фотокатода электроны попадают в однородное магнитное поле с индукцией 0,4 мТл перпендикулярно линиям индукции поля и движутся по окружности радиуса 10 мм. Чему равны длина волны и частота света, падающего на катод с работой выхода 2,5 эВ? Найти период обращения электронов в магнитном поле.

1.54  До какого максимального заряда заряжается шар радиусом 5 см при освещении его светом, длиной волны 0,1 мкм, если работа выхода электронов с поверхности шара 5,5 эВ?

1.55  При освещении шарика радиусом 1 см, покрытого селеном, шарик зарядился до 6 · 10-3 нКл. Какой длины волны использовался свет, если работа выхода из селена равна 9 · 10-19 Дж?

1.56  В вакууме находятся два покрытых кальцием электрода, к которым подключен конденсатор. При освещении катода светом с длиной волны 0,3 мкм на конденсаторе накапливается заряд 10 нКл. Какова емкость конденсатора? Работа выхода электронов из кальция 2,7 эВ.

1.57  Найти заряд на обкладках конденсатора емкостью 8 · 10-3 мкФ, подключаемого к двум электродам, находящимся в вакууме, при освещении одного из них (катода) светом частотой 1015 Гц. Работа выхода электронов на катоде 2,5 эВ.

1.58  К катоду и аноду, находящимся в вакууме, подключён конденсатор емкостью 5 · 103 пФ. При освещении катода с работой выхода 2 эВ на конденсаторе накопился заряд 15 нКл. Определить длину волны света, падающего на катод.

1.59  Фотокатод с работой выхода 3 эВ освещается светом длиной волны 0,15 мкм. Выбиваемые из катода электроны вылетают под углом 60° в магнитное поле с индукцией 0,5 мТл. Какова траектория движения электронов? Рассчитать её параметры.

1.60  Электроны, вылетающие из фотокатода (с работой выхода 2,7 эВ) при освещении светом частотой 2 · 1015 Гц, попадают в магнитное поле с индукцией 2 мТл и движутся по спирали радиуса 2 мм. Под каким углом вылетают электроны в магнитное поле? Каковы период обращения электронов и шаг спирали?

1.61  При освещении фотокатода светом длиной волны 0,4 мкм задерживающее напряжение равно 1,19 В и при 0,5 мкм 0,57 В. По данным рассчитать постоянную Планка и "красную" границу фотоэффекта.

1.62  "Красная" граница фотоэффекта для вольфрама 2,75 · 10-7 м. Найти работу выхода, наибольшую скорость фотоэлектронов и наибольшую энергию этих электронов при использовании света длиной волны 0,18 мкм.

1.63  При соударении фотона со свободным электроном угол рассеяния оказался равным 60°. Найти изменение длины волны фотона.

1.64  Фотон с частотой 1,5 · 1019 Гц соударяется со свободным электроном так, что угол рассеяния равен 80°. Найти длину волны кванта света после соударения.

1.65  Найти кинетическую энергию электрона отдачи при эффекте Комптона, если изменение длины волны фотона частотой

1.66  Найти импульс электрона отдачи при эффекте Комптона, если длина волны фотона частотой 4,5 · 1019 с-1 после взаимодействия с электроном увеличилась на 0,03.

1.67  При комптоновском рассеянии рентгеновского кванта угол рассеяния и длина волны рассеяния излучения равна 45° и 0,25 соответственно. Каковы были длина волны и частота падающего кванта?

1.68  При эффекте Комптона изменение длины волны рентгеновского кванта оказалось равным удвоенной комптоновской длине волы. Каков угол рассеяния фотона?

1.69  При эффекте Комптона угол рассеяния оказался равным 90° и изменение длины волны рассеянного кванта составило 0,022 . Рассчитать по этим данным массу покоя электрона.

1.70  Найти энергию и импульс падающего кванта, если при угле рассеяния 90° половина энергии этого кванта отдаётся электрону.

1.71  При эффекте Компптона угол рассеяния оказался и энергия рассеянного кванта – равной половине энергии падающего. Каков импульс рассеянного кванта?

1.72  Определить кинетическую энергию электрона отдачи при падении на него рентгеновского кванта с энергией 2 МэВ и рассеянии по углом 30°.

2.1. Пылинка массой 1 мг с плотностью воды движется со скоростью 10 м/с. Следует ли при расчёте кинематических и динамических характеристик движения учитывать её волновые свойства?

2.2. Найти длину волны нейтрона, движущегося со скоростью 2·103 м/с. Проявляет ли он при своем движении волновые свойства?

2.3. Дробинка массой 0,1 г летит со скоростью 200 м/с. Определить длину волны де Бройля, связанную с движущейся дробинкой. Следует ли при описании движения дробинки учитывать её волновые свойства?

2.4. В современных ускорителях электроны могут быть разогнаны до скоростей 2·108 м/с. Определить соответствующую этому движению длину волны де Бройля, учитывая изменение массы электрона со скоростью.

2.5. Напряжение на электронно-лучевой трубке достигает 6 кВ. Чему равна длина волны де Бройля в процессе ускорения электрона?

2.6. На грань кристалла падает под углом 60° к поверхности грани параллельный пучок электронов, движущихся с одинаковой скоростью. Определить скорость электронов, если они испытывают дифракционное отражение первого порядка. Расстояние между атомными плоскостями кристалла 2.

2.7. Пучок электронов падает на грань монокристалла под углом скольжения 30°. Отраженные электроны наблюдаются под углом, равным углу падения. Определить ускоряющую разность потенциалов, при которых возникает максимум 3-го порядка. Соответствующее межплоскостное расстояние равно 2,4.

2.8. В одном из опытов по отражению электронов от монокристалла никеля максимум 4-го порядка наблюдался в направлении, составляющем угол 55° с направлением падающих электронов при энергии последних 180 эВ. Вычислить расстояние между атомными плоскостями, соответствующее данному отражению.

2.9. Параллельный пучок электронов, движущихся с одинаковой скоростью 1 Мм/с, падает нормально на диафрагму с длинной щелью шириной 0,1 мкм. Проходя через щель, электроны рассеиваются и образуют дифракционную картину на экране, расположенном на расстоянии 50 см от щели и параллельном плоскости диафрагмы. Определить линейное расстояние между первыми дифракционными минимумами.

2.10. Узкий пучок электронов, прошедших ускоряющую разность потенциалов 30 кВ, падает нормально на тонкий листок золота, проходит через него и рассеивается. На фотопластинке, расположенной за листком на расстоянии 20 см от листка, получена дифракционная картина, состоящая из круглого центрального пятна и ряда концентрических окружностей. Радиус первой окружности 3,4 мм. Определить постоянную кристаллической решетки золота.

2.11. В опыте по дифракции электроны прошли ускоряющую разность потенциалов 100 В. Определите длину волны де Бройля электронов. На объектах каких размеров можно наблюдать дифракцию электронов?

2.12. Найти длину волны де Бройля:

а) для электрона, летящего со скоростью 1 Мм/с;

б) шарика массой 1 г, движущегося со скоростью 1 см/с.

2.13. Если допустить, что неопределённость координаты движущейся частицы равна дебройлевсой длине волны, то какова будет относительная неточность ΔР / Р импульса этой частицы?

2.14. Кинетическая энергия электрона в атоме водорода составляет величину порядка 10 эВ. Используя соотношение неопределенностей, оценить максимальные линейные размеры атома.

2.15. Электрон с кинетической энергией 15 эВ находится в металлической пылинке диаметром 1 мкм. Оценить (в процентах) относительную неточность, с которой может быть определена скорость электрона.

2.16. Используя соотношение неопределенностей, найти выражение, позволяющее оценить минимальную энергию электрона, находящегося в одномерной потенциальной яме шириной l.

2.17. Используя соотношение неопределенностей, оценить низший энергетический уровень электрона в атоме водорода. Принять линейные размеры атома l ~ 1.

2.18. Протон находится внутри бесконечно глубокой одномерной потенциальной ямы шириной 10-5м. Найти минимальное значение энергии протона и определить величину дополнительной энергии, необходимой для перехода его в более высокое энергетическое состояние.

2.19. Минимальное значение энергии α-частицы, находящейся в бесконечно глубокой одномерной потенциальной яме, равно 2 МэВ. Определить ширину ямы.

2.20. Электрон находится внутри бесконечно глубокой одномерной потенциальной ямы, ширина которой соизмерима с размером атома. Оценить величину минимально возможной энергии электрона и минимальное значение энергии, соответствующей изменению его состояния.

2.21. Определить тип частицы, находящейся в бесконечно глубокой одномерной потенциальной яме и имеющей минимально возможное значение энергии 2,05 · 10-2 эВ. Ширина ямы 0,2 нм.

2.22. Оценить ширину потенциальной ямы, в которой находится электрон, если минимальная величина его энергии в яме равна 0,2 МэВ.

2.23. Нейтрон находится в третьем энергетическом состоянии внутри бесконечно глубокой одномерной потенциальной ямы шириною 1. Определить вероятность его пребывания в первой трети ширины ямы.

2.24. Найти вероятность нахождения протона на второй трети ширины бесконечно глубокой одномерной потенциальной ямы. Частица находится в четвертом энергетическом состоянии. Ширина ямы равна 10 нм.

2.25. Найти вероятность пребывания нейтрона, находящегося во втором энергетическом состоянии, в интервале первой трети ширины потенциальной ямы шириною 3 · 10-6м.

2.26. Электрон находится в бесконечно глубокой одномерной яме шириной 4 · 10-6m. Найти вероятность пребывания электрона в третьей четверти ямы. Электрон имеет энергию, соответствующую главному квантовому числу п = 2.

2.27. На пути электрона с энергией 20 эВ находится бесконечно длинный потенциальный барьер высотою 10 эВ. Найти ве­роятность того, что электрон не окажется внутри этого барьера.

2.28. На пути электрона с энергией 15 эВ находится бесконечно длинный потенциальный барьер высотою 10 эВ. Найти вероятность того, что электрон окажется внутри этого барьера.

2.29. Электрон с импульсом 2,4 ·10-24 кг · м/с налетает на потенциальный барьер высотою 15 эВ. Найти вероятность того, что электрон не проникнет внутрь барьера, т. е. отразится.

2.30. Высота потенциального барьера составляет 90 % энергии налетающего на него электрона. Найти коэффициенты преломления, отражения и прозрачности барьера.

2.31. На пути протона с энергией 10 кэВ находится потенциальный барьер, коэффициент преломления которого для протона равен 0,5. Какова высота потенциального барьера?

2.32. Нейтрон с энергией 5 кэВ подлетает к потенциальному барьеру высотой 4 кэВ. Найти вероятность отражения нейтрона.

2.33. α-частица с энергией 20 кэВ налетает на бесконечно длинный потенциальный барьер, высота которого составляет 80 % от энергии α-частицы. Найти изменение длины волны α-частицы и вероятность того, что α-частица просочится внутрь этого барьера.

2.34. Импульс протона 10-21 кг · м/с. Высота потенциального барьера 0,2 МэВ. Найти вероятность того, что протон окажется внутри барьера.

2.35. Коэффициент преломления электрона на потенциальном барьере высотою 50 эВ составляет 0,5. Найти импульс, энергию и длину волны электрона.

2.36. Коэффициент преломления потенциального барьера для протона энергией 8,01 МэВ составляет 0,2. Найти коэффициенты прозрачности и отражения барьера.

2.37. Дебройлевская частица массой 10-14 мг подлетает со скоростью 0,16 Мм/с к потенциальному барьеру 400 МэВ. Найти коэффициент прозрачности барьера и длину волны частицы при переходе через барьер.

2.38. В космических лучах позитроны движутся со скоростями, составляющими 0,95 скорости света в вакууме. Определить соответствующую этому движению длину волны де Бройля, учитывая изменение массы позитрона со скоростью.

2.39. В космических лучах протон движется со скоростью, составляющей 90 % скорости света в вакууме. Определить для протона длину волны де Бройля.

2.40. В ускорителях элементарных частиц электроны могут быть разогнаны до скоростей, соответствующих длине волны де Бройля, равной 1,17 им. С какой скоростью движутся электроны?

2.41. В ускорителях элементарных частиц протоны разгоняются до скоростей, соответствующих длине волны де Бройля, равной 10-15 м. До какой скорости разгоняются протоны?

2.42. В космических лучах нейтрон движется со скоростью, составляющей 0,9 скорости света в вакууме. Определить длину волны нейтрона.

2.43. Нейтроны, движущиеся в космических лучах, характеризуются длиной волны, равной 10-15м. Сравнить скорость нейтронов со скоростью света в вакууме.

2.44. Электроны в ускорителях элементарных частиц характеризуются длиной волны де Бройля λе = 10-12 м. Как изменилась масса микрочастицы?

2.45. В космических лучах нейтрон движется со скоростью, соответствующей длине волны λ = 0,8 · 10-15 м. Во сколько раз увеличилась масса нейтрона?

2.46. В ускорителях элементарных частиц протон может быть разогнан до скорости, соответствующей длине волны де Бройля, равной λ = 0,75 · 10-15 м. Чему равна масса частицы?

2.47. Какова вероятность пребывания позитрона, характеризующегося минимально возможной энергией, во второй половине ширины бесконечно глубокой одномерной потенциальной ямы шириной 2 · 10-9 м?

2.48. Нейтрон находится во втором энергетическом состоянии внутри бесконечно глубокой одномерной потенциальной ямы шириной 0,8 · 10-8 м. Какова вероятность пребывания микрочастицы в первой половине ширины ямы?

2.49. Протон находится в третьем энергетическом состоянии внутри бесконечно глубокой одномерной потенциальной ямы шириной 4 · 109 м. Какова вероятность пребывания микрочастицы во второй трети ширины ямы?

2.50. Найти вероятность пребывания электрона, находящегося в четвертом энергетическом состоянии, в третьей четверти ширины бесконечно глубокой одномерной потенциальной ямы шириной 3 · 10-9 м?

2.51. α-частица находится во втором энергетическом состоянии внутри бесконечно глубокой одномерной потенциальной ямы шириной 0,6 · 10-8 м. Какова вероятность пребывания α-частицы в третьей трети ширины ямы?

2.52. Какова вероятность пребывания позитрона, имеющего энергию, соответствующую главному квантовому числу, равному четырем, во второй трети ширины бесконечно глубокой одномерной потенциальной ямы шириной 5 · 10-9 м?

2.53. Найти импульс позитрона, имеющего частоту 3· 1021 Гц.

2.54. Каков импульс α-частицы, имеющей частоту 1,2 · 1022 Гц.

2.55. Микрочастица движется со скоростью, равной 0,8 скорости света в вакууме, и характеризуется длиной волны 10-15 м. Чему равна масса "покоя" частицы? Указать тип частицы.

2.56. Найти импульс позитрона, имеющего частоту1,65 · 1018 Гц.

2.57. Чему равна масса "покоя" микрочастицы, движущейся со скоростью, равной 0,75 скорости света в вакууме, и характеризующейся длиной волны 1,165 · 10-15 м? Указать тип частицы.

2.58. Определить тип частицы, находящейся в бесконечно глубокой одномерной потенциальной яме и имеющей минимально возможное значение энергии 1,92 · 105 эВ. Ширина ямы 1,4 пм.

2.59. Оценить ширину потенциальной ямы, в которой находится протон, если минимальная величина его энергии в яме равна 8,6 МэВ.

2.60. На пути нейтрона с энергией 0,25 МэВ находится бесконечно длинный потенциальный барьер высотою 0,17 МэВ. Найти вероятность того, что нейтрон не окажется внутри этого барьера.

2.61. Коэффициент преломления электрона на потенциальном барьере высотою 50 эВ составляет 0,3. Найти импульс, энергию и длину волны электрона.

2.62. Протон с энергией 15 кэВ подлетает к потенциальному барьеру высотой 9 кэВ. Найти вероятность отражения протона.

2.63. Электрон с импульсом 2,8 · 10-24 кг · м/с налетает на потенциальный барьер высотою 23 эВ. Найти вероятность того, что электрон не проникнет внутрь барьера, т. е. отразится.

2.64. На пути протона с энергией 8,8 кэВ находится потенциальный барьер, коэффициент преломления которого для протона равен 0,8. Какова высота потенциального барьера?

2.65. На пути α-частицы с энергией 35 кэВ находится бесконечно длинный потенциальный барьер высотою 20 кэВ. Найти вероятность того, что α-частица окажется внутри этого барьера.

2.66. Дебройлевская частица массой 10-15 мг подлетает со скоростью 0,1 Мм/с к потенциальному барьеру 14 МэЭ. Найти коэффициент прозрачности барьера и длину волны частицы при переходе через барьер.

2.67. α-частица с энергией 15 кэВ налетает на бесконечно длинный потенциальный барьер, высота которого составляет 75 % от энергии α-частицы. Найти изменение длины волны α-частицы и вероятность того, что α-частица просочится внутрь этого барьера.

2.68. Коэффициент преломления потенциального барьера для нейтрона с энергией 4,67 МэВ составляет 0,3. Найти коэффициенты прозрачности и отражения барьера.

2.69. Импульс нейрона 10-20 кг · м/с. Высота потенциального барьера 0,05 МэВ. Найти вероятность того, что нейрон окажется внутри барьера.

2.70. Высота потенциального барьера составляет 80% энергии налетающего на него позитрона. Найти коэффициент преломления, отражения и прозрачности барьера.

2.71. Ядро атома лития с энергией 185 кэВ налетает на потенциальный барьер с коэффициентом преломления 0,37. Чему равна высота этого потенциального барьера?

2.72. Высота потенциального барьера составляет 66,7 % энергии налетающей на него микрочастицы массой, равной 5,8 10-25 кг. Каковы коэффициенты прозрачности, преломления и отражения барьера?

3.1. Вычислить полную энергию, орбитальный момент импульса и магнитный момент электрона, находящегося в 2/р-состоянии в атоме водорода.

3.2. Атом водорода, находившийся первоначально в основном состоянии, поглотил квант света и перешел в р-состояние. Определить изменение момента импульса орбитального движения электрона.

3.3. Определить момент импульса и его проекцию на заданное направление электронов, находящихся в состоянии: a) 3s ; б) 2р.

3.4. Определить возможные значения магнитного момента, обусловленного орбитальным движением электрона в возбужденном атоме водорода, если энергия возбуждения 12,09эВ.

3.5. Определить число электронов в атомах, у которых в нормальном состоянии заполнены:

а) К — и L— слои, 3s-оболочки и наполовину 3р-оболочка; б) К-, L— и М-слои и 4s-, 4р— и 4d-оболочки.

3.6. Сколько s-, p-, d-электронов может находиться в К-, L-, М-слое?

3.7. В атоме К-, L-, и М-слои заполнены целиком. Определить: а) общее число электронов в атоме; б) число s-, р-, d-электронов; в) сколько p-электронов имеют квантовое число т — 0?

3.8. Определить порядковый номер атома в таблице Менделеева, если число s-электронов атома равно числу d -электронов.

3.9. Определить механические, магнитные моменты и их проекции 2s—электронов атома.

3.10. Найти проекции собственных моментов электронов атома циркония на направление внешнего магнитного поля индукцией 0,1 мТл.

3.11. Сколько электронов в атоме железа имеют орбитальный магнитный момент, равный нулю? Найти орбитальный механический момент внешних электронов атома.

3.12. Сколько электронов в атоме кобальта имеют орбитальный магнитный момент, равный нулю? Чему равно значение орбитального магнитного момента электронов атома, находящихся на внешнем уровне.

3.13. Найти изменение механического момента движения электрона вокруг ядра атома натрия при переходе с 3s-уровня на 2s-уровень, на 2р-уровень.

3.14. Электрон в атоме магния переходит с Зs-уровня на 2р-уровень. Как изменяются при этом орбитальные механический и магнитный моменты электрона?

3.15. Определить изменение моментов и их проекций электронов при переходе с 2р-уровня на 2s-уровень.

3.16. Определить границы серии Лаймана и серии Бальмера.

3.17. Какие переходы электронов в атоме водорода сопровождаются излучением видимой области спектра? Чему равны соответствующие длины волн?

3.18. Свет от газоразрядной трубки с водородом, возникающий в результате перехода электронов с четвертого уровня в серии Бальмера, падает на дифракционную решётку с периодом 2 · 10-3 мм. Определить, под каким углом видна данная линия в спектре первого порядка.

3.19. На дифракционную решетку с периодом 5 · 10-3 мм нормально падает свет от газоразрядной трубки, наполненной водородом. В спектре четвёртого порядка спектральная линия видна под углом 21°24′. Какому переходу электрона в атоме водорода соответствует данная спектральная линия?

3.20. На сколько изменяется энергия атома водорода в результате перехода электрона с 6-го уровня в серии Бальмера?

3.21. Какую наименьшую скорость должны иметь электроны, чтобы при возбуждении атомов водорода ударами таких электронов появились все линии спектра водорода?

3.22. На дифракционную решетку с постоянной 2 мкм падает свет от разрядной трубки, наполненной водородом. Одна из линий в спектре первого порядка соответствует углу дифракции 14°10′. Какому переходу электрона соответствует эта линия?

3.23. Чему равна постоянная дифракционной решетки, посредством которой наблюдается спектр атомарного водорода, если третья линия в спектре второго порядка соответствует углу дифракции 12°30′.

3.24. Какую энергию должен иметь электрон, чтобы при возбуждении атомов водорода ударами таких электронов спектр водорода имел только одну спектральную линию?

3.25. Частота излучения одной из линий серии Бальмера атома водорода равна 6,17 · 1014 Гц. Вычислить значения ближайших двух частот этой серии.

3.26. Сколько спектральных линий наблюдается в спектре водорода, атомы которого находятся в четвёртом возбужденном состоянии. Найти максимальную и минимальную частоты этого спектра.

3.27. Электрон атома гелия находится на третьем энергетическом уровне. Сколько квантов с различными энергиями могут излучать атомы? Найти их длины волн.

3.28. Определите длину волны, излучаемую при переходе электрона в ионе гелия из стационарного состояния с номером 4 в состояние с номером 2.

3.29. Электрон в невозбужденном атоме водорода получил энергию 13,0 эВ, На какой энергетический уровень он перешёл?

3.30. В атоме водорода электрон переходит с 5 уровня на 2 уровень. Излучение, возникающее при этом, падает нормально на дифракционную решетку с числом штрихов 5 · 105 м-1. Под какими наименьшими и наибольшими углами наблюдаются дифракционные линии, соответствующие такому переходу электронов в атоме водорода?

3.31. Электрон в атоме водорода находится на 4 уровне. Какие наименьшие и наибольшие частоты могут наблюдаться в спектре излучения атома?

3.32. Определить изменение энергии атома водорода в результате перехода электрона со 2 уровня на 5 уровень.

3.33. Определите длину волны света, испускаемого атомом натрия при переходе из первого возбуждённого состояния в основное состояние.

3.34. Определить длину волны коротковолновой границы сплошного рентгеновского спектра, если известно, что при увеличении ускоряющего напряжения на трубке в 2 раза она изменилась на 0,5.

3.35. Определить скорость электронов, падающих на антикатод рентгеновской трубки, если минимальная длина волны в сплошном спектре рентгеновских лучей равна 10.

3.36. При увеличении напряжения на рентгеновской трубке в 2 раза граница тормозного спектра сместилась на 10-10м. Каково было значение границы тормозного спектра? Найти смещение границы по частоте.

3.37. Найти значение экранирующей постоянной, если при переходе Кβ в атоме никеля (Z = 28) излучение имеет частоту 2,133 · 1018 Гц.

3.38. Граница тормозного спектра по частоте сместилась с сторону уменьшения на 20 %. Как изменилось напряжение в рентгеновской трубке?

3.39. Какое вещество использовано в качестве анода в рентгеновской трубке, если переход Кα сопровождается излучением длиною волны 1,667 · 10-10 м?

3.40. Определить тип перехода электронов в атоме кобальта (Z = 27), если экранирующая постоянная равна 1 и излучение имеет волновое число 0,556 · 1010 м-1.

3.41. Найти длину волны характеристического рентгеновского излучения, соответствующую Lβ-переходу в атоме висмута.

3.42. Волновое число Lβ-линий характеристического рентгеновского излучения равно 15,375 · I07 м-1.

3.43. При уменьшении напряжения на рентгеновской трубке в 3 раза коротковолновая граница сплошного рентгеновского спектра смес­тилась на 1 . Чему была равна длина волны границы спектра?

3.44. С какого уровня в атоме с Z = 41 переходит электрон на низший уровень, если этот переход сопровождается излучением с волновым числом 1,65 · 1010 м-1?

3.45. Найти величины коротковолновой границы непрерывного рентгеновского спектра, если при уменьшении напряжения, приложенного к рентгеновской трубке, на 18 кВ значение границы спектра по длине волны изменяется в 2 раза.

3.46. При переходе электрона в атоме с М-слоя на К-слой испускаются рентгеновские лучи с длиной волны 0,4315 . Какой это атом?

3.47. При переходе электрона в атоме с L-слоя на К-слой (σ = 1) испускаются рентгеновские лучи с длиной волны 0,788 . Какой это атом?

3.48. При напряжении на рентгеновской трубке в 28 кВ разность длин волн Ка-линии (σ = 1) и коротковолновой границы сплошного рентгеновского спектра составляет 1. Какой элемент является антикатодом данной трубки?

3.49. Определить, в результате какого перехода возникает одна из линий К-серий алюминия (7,97). Постоянная экранировки равно 1,65.

3.50. Длина волны Ка-линии для магния равна 9,87. Вычислить постоянную экранирования.

3.51. В рабочем теле лазера на длине кристаллу 1см интенсивность электромагнитного излучения увеличилась в 1000 раз. Найти коэффициент усиления рабочего тела лазера.

3.52. Коэффициент усиления рабочего тела лазера равен 114 м-1. Во сколько раз изменяется интенсивность электромагнитного излучения на пути 1,10 см?

3.53. Электромагнитное излучение лазера длиной волны 6943на длине кристалла рубина увеличивается в 104 раз. Каков путь излучения в кристалле, если коэффициент усиления рабочего тела равен 4,1 · 102 м-1?

3.54. Интенсивность света в веществе на пути 5 см уменьшилась в 2 раза. Найти коэффициент поглощения вещества.

3.55. Коэффициент поглощения вещества равен 2,3 м-1. Во сколько раз изменилась интенсивность света на пути 10 см?

3.56. Определить порядковый номер атома в таблице Менделеева, если в атоме К-, L,-слои заполнены полностью, а в М-слое для полного его заполнения недостает трех электронов.

3.57. Определить границы серии Пашеиа электромагнитного излучения атомов водорода.

3.58. На дифракционную решетку с периодом 3 · 10-3 мм падает свет от газоразрядной трубки с водородом, возникающим при переходе электрона с пятого уровня в серии Бальмера. Под какими углами наблюдаются линии этого излучения в дифракционных спектрах 1-го и 2-го порядков?

3.59. Определить длину волны излучения атома гелия при переходе электронов из состояния с номером 3 в состояние с номером 2.

3.60. Электроны в атомах водорода находятся на 3-м энергетическом уровне. Волны каких частот может излучать атом?

3.61. Определить, как изменится напряжение на рентгеновской трубке при смещении границы тормозного излучения на 30 % в сторону увеличения длины волны.

3.62. Определить длину волны и частоту видимого света, возникающего при переходе электрона в атоме водорода с 5-го уровня.

3.63. В результате перехода электрона в атоме водорода с 5-го уровня в серии Бальмера в дифракционном спектре четвертого порядка наблюдается спектральная линия под углом 23°. Определить период дифракционной решетки.

3.64. Дифракция света, полученного от газоразрядной трубки с водородом, наблюдается на решетке с периодом 1 мкм. Какому переходу в атоме соответствует линия в спектре 1-го порядка, расположенная под углом 29°20′?

3.65. В атоме вещества К-, L-, М-слои заполнены полностью, в N-слое находится три электрона. Какой это атом?

3.66. Найти коэффициент поглощения вещества, в котором интен­сивность излучения уменьшается в три раза на толщине 3 см.

3.67. Во сколько раз изменится интенсивность света в веществе толщиною 5 см с коэффициентом поглощения 2,5 м-1 ?

3.68. При уменьшении напряжения, приложенного к рентгеновской трубке на 20 кВ, коротковолновая граница тормозного спектра изменилась в 2,3 раза. Чему были равны частота и длина волны коротковолновой границы?

3.69. Определить длину полны рентгеновского излучения, воз­никающего при переходе электрона в атоме циркония с L-слоя на K-слой. Принять значение экранирующей постоянной, равным 1.

3.70. Электрон в атоме с Z = 41 переходит с четвертого уровня на низший. Чему равно волновое число этого излучения?

3.71. При каком напряжении на трубке, имеющей молибденовый анод, разность длин волн границы К-серии и коротковолновой границы сплошного рентгеновского спектра составляет 0,283 ?

3.72. Определить длину волны К-серии излучения атома алюминия при переходе с третьего энергетического уровня, приняв постоянную экранирования, равной 1,65.

4.1. В качестве примеси в кристалл германия взяли атомы фосфора. Каким типом проводимости обладает полученный примесный полупроводник?

4.2. Определить тип проводимости следующих соединений: 1 – германий – галлий; 2 – германий – мышьяк 3 – германий – индий.

4.3. Определить ширину валентной зоны для меди при абсолютном нуле температуры и максимальную скорость свободных электронов, полагая, что на каждый атом приходится по одному свободному электрону.

4.4. Определить число свободных электронов на атом алюминия, граничная энергия для которых равна 11,7 эВ.

4.5. Во сколько раз нужно повысить абсолютную температуру про­водника от 0 ºС, чтобы его сопротивление увеличилось в 3 раза?

4.6. Найти вероятность заполнения электронами уровня с энергией 0,6 эВ в металле, имеющем энергию уровня Ферми, равную 0,5 эВ, при температуре 580 К.

4.7. Металл имеет энергию Ферми, равную 1,2 эВ при температуре 307 ºС. Найти вероятности заполнения электронами уровней с энергиями 1,3 и 1,1 эВ.

4.8. До какой температуры был нагрет проводник от 0 ºС, если его сопротивление возросло в два раза?

4.9. Металл имеет энергию Ферми, равную 0,7 эВ. Найти вероятность заполнения электронами уровня Ферми при температуре 473 К.

4.10. Вероятность заполнения электронами уровня с энергией 0,7 эВ при температуре 307 ºС равна 0,12. Найти энергию Ферми металла.

4.11. При температуре 580 К вероятность заполнения электронами некоторого уровня в металле равна 0,88. Найти энергию этого уровня, если энергия Ферми равна 1 эВ.

4.12. Определить вероятность заполнения электронами уровня металла с энергией 0,15 эВ при температуре 887 ºС. Энергия уровня Ферми металла при этой температуре равна 0,1 эВ.

4.13. Определить концентрацию свободных электронов натрия при Т= 0 К, если энергия Ферми равна 3,07 эВ.

4.14. Вычислить суммарную кинетическую энергию свободных электронов в 1 см серебра при абсолютном нуле температуры, считая, что на каждый атом приходится один свободный электрон.

4.15. При 0 °С удельное сопротивление полупроводника 0,1 Ом · м, а проводника в 10000 раз меньше. Оценить, при какой температуре сопротивление полупроводника станет меньше сопротивления проводника. Нагрев веществ проводится в равных условиях. Принять, что температурный коэффициент сопротивления проводника равен 1/273 град-1, ширина запрещенной зоны полупроводника равна 0,8 эВ и не зависит от температуры.

4.16. Вычислить плотность свободных электронов и дырок для кремния с собственной проводимостью при 27 ºС, имеющего при этой температуре ширину запрещенной зоны 1,08 эВ. Эффективные массы электронов и дырок принять равными массе покоя электрона те.

4.17. Удельное сопротивление собственного германия при комнатной температуре равно 0,47 Ом · м. Полагая, что подвижности электронов и дырок соответственно равны 0,38 и 0,18 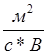, вычислить плотность носителей тока собственного Ge.

4.18. Во сколько раз отличаются изменения сопротивлений полупроводника и проводника при изменении температуры от 0 до 100 ºС? Принять ширину запрещенной зоны полупроводника 1,0 эВ и температурный коэффициент сопротивления проводника 1/273 град-1 не зависящими от температуры.

4.19. Удельное сопротивление полупроводника при 0 ºС равно 0,1 Ом · м, что в 100000 раз больше, чем у проводника при той же температуре. Как изменится отношение сопротивлений веществ при их нагревании до 800 ºС? Считать, что ширина запрещенной зоны полупроводника равна 0,9 эВ и температурный коэффициент сопротивления проводника 1/273 град-1 в этом интервале температур остаются постоянными.

4.20. В чистом Ge при температуре 300 К подвижность электронов равна 0,38 . Найти удельное сопротивление полупроводника про этой температуре и подвижность носителей заряда при 30 К, считая, что подвижность меняется с температурой по закону и = аТ-3/2 , где а — постоянная, отношение подвижностей электронов и дырок принять равным 3,3. Эффективная масса электрона равна 0,56 те, эффективная масса дырки 0,37 те. Считая, что ширина запрещенной зоны линейно изменяется с температурой ΔЕ = (0,785 – 4 · 10-4 Т) эВ, определить энергию Ферми при 30 и 300 К.

4.21. Найти ширину запрещенной зоны и энергию Ферми в собственном Ge при температурах 0 и 300 К. Считать, что ширина запрещенной зоны меняется с температурой по закону ΔЕ = (0,785 — 4 · 10-4 Т) эВ, а эффективные массы электронов и дырок равны соответственно 0,56 mе и 0,37 тe. Определить концентрацию электронов и дырок при 300 К.

4.22. Предполагая, что эффективные массы электронов и дырок одинаковы, вычислить положение уровня Ферми относительно дна зоны проводимости для кристалла GaAs с шириной запрещенной зоны 1,428 эВ, используемой в полупроводниковых лазерах.

4.23. Определить вероятность заполнения электронами энергетического уровня кристалла проводника с энергией 12,12 эВ при температуре 500 К. Энергия Ферми проводника равна 12,18 эВ.

4.24. При температуре 300 К вероятность заполнения уровня Ферми в кристалле проводника равна 1/2. Электрон находится на уровне, вероятность заполнения которого равна 1/3. Определить разность энергии данного уровня и уровня Ферми.

4.25. Энергия Ферми кристалла равна 11,85 эВ. Определить вероятность заполнения электронами энергетического уровня с энергией 11,93 эВ при температуре 700 К.

4.26. Как изменится вероятность заполнения электронами энергетического уровня, лежащего выше уровня Ферми на 10-2 эВ, при повышении температуры 300 К в 2 раза?

4.27. Определить максимальную скорость и концентрацию свободных электронов кристалла при 0 К, имеющего энергию Ферми 12,8 эВ.

4.28. Концентрация свободных электронов 5,3 · 1028 м-3. Определить энергию Ферми металла при 0 К.

4.29. Определить энергию Ферми металла при температуре 327 ºС, если при абсолютном нуле концентрация свободных электронов равна 1,44 · 1029 м-3.

4.30. Определить, на сколько изменяется энергия Ферми серебра при нагревании его от абсолютного нуля до 800 К, если при 0 К концентрация свободных электронов равна 6 · 1028 м-3.

4.31. Концентрация свободных электронов алюминия при абсолютном нуле температуры равна 1,5 · 109 м-3. Как изменится энергия Ферми при нагревании вещества до 500 ºС?

4.32. Найти отношение энергии Ферми меди при абсолютном нуле температур и 800 К, если концентрация свободных электронов кристалла при 0 К равна 8,2 · 1028 м-3 .

4.33. При некоторой температуре в электрическом поле напряженностью 0,1 кВ/м вектор плотности тока в меди равен 6,8 · 109 А/м2. Определить удельное сопротивление меди при этих условиях.

4.34. В электрическом поле напряженностью 50 В/м при некоторой температуре плотность тока в кристалле серебра равна 3,2 · 109 А / м2. Найти длину свободного пробега электронов серебра. Принять равными значения энергии Ферми 5,5 эВ и концентрации свободных электронов 6,25 · 1028м3.

4.35. Найти длину свободного пробега электронов на уровне Ферми в кристалле алюминия (энергия Ферми 11,9 эВ, концентрация свободных электронов 1,5 · 1029 м-3, удельное сопротивление 2,45· 10-8 Ом · м).

4.36. При абсолютном нуле температуры концентрация свободных электронов в металле равна 1028 м-3. Как изменится энергия Ферми вещества при нагревании его от 0 до 1000 К?

4.37. Определить изменение энергии Ферми проводника при повышении его температуры от 100 до 500 ºС, если при абсолютном нуле температуры металл имеет концентрацию свободных электронов 1027 м-3.

4.38. Длина свободного пробега электронов серебра при некоторой температуре равна 2 · 10-8м. Определить скорость электронов, находящихся на уровне Ферми, и значение энергии Ферми, приняв концентрацию свободных электронов, равной 1,1 · 1029 м-3, если при напряженности электрического поля 10 В/м плотность тока равна 6 · 108 А/м2.

4.39. Определить подвижность электронов и дырок в собственном проводнике, имеющих концентрацию пар носителей заряда 2 · 1026 м-3 и удельное сопротивление 3 · 10-4 Ом · м, если принять, что подвижность электронов в 4 раза превышает подвижность дырок.

4.40. Скорость движения электронов собственного полупроводника в 5 раз больше, чем дырок, и в электрическом поле с напря­женностью 0,2 кВ / м составляет 7,2 · 103 м/с. Определить кон­центрацию пар электрон-дырка, если при некоторой темпера­туре удельное сопротивление полупроводника 8,76 · 10-4 Ом · м.

4.41. Определить концентрацию пар носителей заряда в кристалле кремния при температуре 327 ºС энергией Ферми, равной 0,9 эВ, приняв эффективные массы электрона и дырки равными массе покоя электрона.

4.42. Концентрация пар носителей заряда в собственном полупроводнике 7 · 1025 м-3. Найти энергию Ферми и ширину запрещенной зоны полупроводника при температуре 500 К (принять эффективные массы электрона и дырки равными массе покоя электрона).

4.43. Концентрация электронов в собственном полупроводнике равна 2 · 1025 м-3 при температуре 320 К. Какую дополнительную энергию должны получить электроны, чтобы стать свободными?

4.44. Полупроводниковый терморезистор при температуре 0 ºС имеет энергию Ферми, равную 0,8 эВ. Чему равен при данных условиях температурный коэффициент сопротивления терморезистора?

4.45. Найти ширину запрещенной зоны полупроводникового терморезистора, имеющего при температуре 0 ºС сопротивление 300 Ом, если при повышении температуры на 50 ºС сопротивление изменилось на 80 Ом.

4.46. При изменении температуры полупроводникового терморезистора от 20 до 100 ºС сопротивление изменилось в 3 раза. Чему равна энергия Ферми собственного полупроводника?

4.47. Ширина запрещенной зоны собственного полупроводника 0,7 эВ. Как изменится сопротивление полупроводника при понижении его температуры от 200 до 150 ºС?

4.48. Температурный коэффициент сопротивления собственного полупроводника при некоторой температуре равен -6,44 · 10-2 К-1. Найти температуру полупроводника, если ширина запрещенной зоны равна 1 эВ.

4.49. Как изменится температурный коэффициент сопротивления собственного полупроводника, если при повышении его температуры от 0 до 100 ºС ширина запрещенной зоны уменьшилась вдвое?

4.50. При некоторой температуре энергия Ферми собственного полупроводника равна 0,3 эВ и температурный коэффициент сопротивления равен -0,02 К-1. Чему равна температура полупроводника?

4.51. Найти энергию Ферми собственного полупроводника, если при температуре 600 К его температурный коэффициент сопротивления равен -0,05 К-1.

4.52. При температуре 300 К температурный коэффициент сопротивления терморезистора равен -3,22 · 10-2 К-1 . Чему равна ширина запрещенной зоны и энергия Ферми этого терморезистора?

4.53. При повышении температуры собственного полупроводника от 20 до 100 ºС температурный коэффициент сопротивления изменился в 2,5 раза. Как изменилось значение энергии Ферми полупроводника?

4.54. При охлаждении собственного полупроводника от 400 до 250 К энергия Ферми изменилась в 1,7 раза. Изменился ли температурный коэффициент сопротивления полупроводника? И если изменился, то как?

4.55. Удельная электропроводимость собственного полупроводника при температуре 0 ºС меньше, чем при температуре 150 ºС в 2 раза. Чему равны энергия Ферми и ширина запрещенной зоны полупроводника?

4.56. Собственный полупроводник имеет энергию Ферми 0,9 эВ. Как изменится его удельное сопротивление при охлаждении от 330 К до 0 ºС?

4.57. Чему равна энергия Ферми собственного полупроводника, если фотоэлектроны в нем возникают под действием света длиной волны 2,0- 10-6м?

4.58. Найти ширину запрещенной зоны собственного полупроводника, если внутренний фотоэффект в нем возможен под действием света частотой 0,15 · 1015 с-1.

4.59. На каком расстоянии отстоит акцепторный уровень от валентной зоны, если дырки фотопроводимости появляются на этом уровне под действием квантов света частотой 0,2 · 1014 Гц?

4.60. В примесном полупроводнике р-типа фотодырки возникают под действием света частотой 0,65 · 1012 Гц и фотоэлектроны под действием света длиною волны 0,46 мкм. Во сколько раз расстояние акцепторного уровня до валентной зоны меньше ширины запрещенной зоны?

4.61. Определить длину свободного пробега электронов алюминия с энергией Ферми 11,5 эВ, если в электрическом поле напряженностью 40 В / м плотность тока равна 2,5 · 109 А / м2 при концентрации свободных электронов 1,4 · 1029 м-3.

4.62. Чему равны температурный коэффициент сопротивления и энергия активации полупроводникового материала терморезистора, если его сопротивление уменьшается в 1,47 раза при увеличении температуры с 300 до 400 К?

4.63. Подвижность свободных электронов в чистом германии при температуре 300 К равна 0,38 . С ростом температуры подвижность электронов увеличивается по закону u = aT-3/2 (где a — постоянная), а концентрация свободных электронов растет по закону 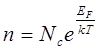. При какой температуре подвижность электронов уменьшится вдвое, а концентрация увеличится вдвое? Температурными зависимостями эффективной плотности состояний в зоне проводимости Nc и положения уровня Ферми ЕF пренебречь. Ширину запрещенной зоны принять постоянной и равной 0,785 эВ.

4.64. Найти минимальную энергию, необходимую для образования пары электрон — дырка в чистом теллуре, если известно, что его электропроводность возрастет в 5,2 раза при увеличении температуры от 300 до 400 К.

4.65. Для зондирования атмосферы используются радиозонды, датчиком температуры в которых является полупроводниковый термистор с шириной запрещенной зоны 0,42 эВ. Радиозонд запущен с поверхности Земли при температуре 27 ºС. Чему равна температура атмосферы на высоте подъема зонда, если сопротивление термистора возросло в 5 раз?

4.66. В лазерном дальномере-бинокле приемником излучения является кремниевый лавинный фотодетектор с шириной запрещенной зоны 1,1 эВ при 20 ºС. Найти максимальную длину волны, которую будет фиксировать бинокль.

4.67. Определить длинноволновую границу чувствительности фоторезистора на основе CdS с энергией Ферми 0,69 эВ.

4.68. Определить ширину запрещенной зоны кремния, если известно, что длинноволновой край полосы поглощения лежит вблизи длины волны 1,11 мкм.

4.69. Определить отношение концентраций свободных электронов в кристаллах алюминия и серебра при 0 К. Энергия Ферми серебра равна 5,5 эВ, алюминия в 2,16 раза больше. Найти концентрацию свободных электронов в кристалле алюминия и найти концентрацию атомов веществ, приняв валентности серебра и алюминия равными 1 и 3 соответственно.

4.70. Вычислить глубину потенциальной ямы для электронов, находящихся в алюминии, полагая, что на каждый атом приходится три свободных электрона.

4.71. Определить концентрацию свободных электронов в кристалле проводника, если энергия Ферми вещества равна 0,9 эВ.

4.72. При нагревании собственного полупроводника с энергией Ферми 0,7 эВ от комнатной температуры его сопротивление изменилось в 5 раз. До какой температуры нагрели полупроводник?

5.1. Определить зарядовое и массовое числа частицы, обозначенной буквой X в символической записи ядерной реакции: а) 6C14 + 2He4 → 8O17 + X, б) 13Al27 + X → 1H1 +12Mg36

5.2. В результате серии радиоактивных распадов ядро урана 92U238 превратилось в изотоп свинца 82РЬ206. Определить сколько α- и β-распадов произошло в результате такого превращения.

5.3. Искусственно полученное радиоактивное семейство, начинающееся трансурановым элементом нептунием 93Np237 , заканчивается висмутом 83Bi209. Сколько α- и β-распадов при этом происходит?

5.4. Какой изотоп образуется из радиоактивного Th232 четырех α- и двух β—распадов?

5.5 Напишите недостающие обозначения в следующих ядерных реакциях: а)18Al27 + 0n1 → ? + 2He‑, б)6C12 + 1H1 →6C13 + ?

5.6. При бомбардировке изотопа азота N14 нейтронами получается изотоп углерода С14, который оказывается β-радиоактивным. Написать уравнение обеих реакций.

5.7. Начальная радиоактивность полония 84Р0210 равна 1010 расп/с. Определить активность и массу полония через 2 месяца.

5.8. Ядро урана U236, захватив один нейтрон, разделилось на два осколка, причем освободилось два нейтрона. Одним из осколков оказалось ядро ксенона Хе140. Определить порядковый номер и массовое число второго ядра. Написать уравнение ядерной реакции.

5.9. При соударении γ-фотона с ядром дейтерия последнее может расщепиться на два нуклона. Написать уравнение ядерной реакции и определить минимальную энергию γ-фотона, способного вызвать такое расщепление.

5.10. Найти энергии ядерных реакций: а) Н3(p,γ) Не4; 7, б) Н2(d,γ) Не4.

5.11. Вычислить дефект масс и энергии связи ядра кислорода, если известно, что тр = 1,00728 а. е.м., тn = 1,00866 а. е.м., Мя = 16,99913 а. е.м.

5.12. Найти суммарную энергию γ-квантов, образующихся при аннигиляции электрона и позитрона.

5.13. Какое количество энергии освободится при соединении одного протона и двух нейтронов в атомное ядро?

5.14. Какое ядро из двух изобаров Li7 и Be7 более прочно?

5.15. Атомное ядро, поглотившее γ-квант(λ = 4,7 · 10-2 ), пришло в возбужденное состояние и распалось на отдельные нуклоны, разлетевшиеся в разные стороны. Суммарная кинетическая энергия нуклонов равна 0,4 МэВ. Определить энергию связи ядра.

5.16. Какова электрическая мощность атомной электростанции, расходующей в сутки 220 г изотопа 92U235 и имеющей КПД 25 %?

5.17. Найти минимальную энергию, необходимую для удаления из ядра 7N14: а) одного нейрона, б) одного протона

5.18. Какую наименьшую энергию нужно затратить, чтобы разделить ядро 2He4 на две одинаковые части?

5.19. Вычислить удельную энергию связи ядра урана 92U238, если Мя = 238,03 а. е.м.

5.20. Вычислить дефект масс и энергию связи ядра 7N14.

5.21. Какая энергия выделится при ядерной реакции 3Li7 + 1H2 → 4Ве8 + 0n1? Известно, что массы ядер равны соответственно: Мn = 2,01355 а. е.м., MLi = 7,01436 а. е.м., МВе = 8,00311 а. е.м.

5.22. Определить энергию, выделяющуюся (поглощаемую) в ядерной реакции 3Li7+ 1p1 → 2 2α4.

5.23. Какая энергия выделяется в термоядерной реакции 1D2 + 1H3 → 2He4 + 0n1?

5.24. Рассчитать энергию, выделившуюся в результате распада одного ядра урана-235 при попадании в него медленного нейтрона. Считать, что реакция идет по такой схеме: 92U253 + 0n1 → 38Sr95 + 54Xe138 +20n1.

5.25. Определить энергию, которая выделилась бы при распаде 1 кг урана-235.

5.26. При взрыве боеприпаса типа "деление-синтез" основной реакцией является реакция на дейтерии и литии: 1D2 + 3Li6 →22He4. Рассчитать энергетический баланс этой реакции. Определить энергию, которая выделилась бы при взрыве 1 кг ядер 1D2 и 3Li6.

5.27. Сравнить энергию, выделившуюся при синтезе 1 г смеси дейтерия и трития, с энергией, которая освобождается при делении 1 г урана. Считать, что при делении каждого ядра урана выделяется энергия порядка 200 МэВ.

5.28. Определить суточный расход U235 на атомной станции мощностью 25 МВт, полагая КПД электростанции равным 20 %. Энергию, выделяющуюся при одном акте деления, принять равной 200 МэВ.

5.29. Рассчитать суточный расход топлива ядерным реактором тепловой мощностью в 260 МВт. Топливом считать обогащенный уран с содержанием U235 20 кг/т, причем вследствие захвата нейтронов делению подвергается 85 % всех ядер.

5.30. Подводная лодка имеет мощность атомных установок 14,7 МВт, топливом служит обогащенный уран (25 % U235). Определить запас горючего, необходимого для 6-месячного плавания лодки.

5.31. Вычислить массу изотопа U235, подвергающегося делению при взрыве атомной бомбы, тротиловый эквивалент которой 30000 т. Тепловой эквивалент тротила считать равным 4,18 ·103кДж · кг-1.

5.32. Вычислить суммарную кинетическую энергию, с которой разлетаются продукты ядерной реакции Li7 (p, 2а), если энергия бомбардирующих протонов равна 5 МэВ. Определить также скорость α-частиц.

5.33. Найти массу полония 84Po210, активность которого равна 17,4 · 1010 расп/с.

5.34. Постоянная распада радиоактивного изотопа 1,44 · 10-3 ч-1. Через сколько времени распадётся 40 % первоначального количества атомов?

5.35. Период полураспада изотопа стронция 38Sr90 равен 28 годам. Через сколько лет активность изотопа уменьшится в 5 раз? Какая часть ядер распадётся за это время?

5.36. Для определения объёма крови человека ему вводят небольшое количество раствора, содержащего изотоп 11Na24 с активностью 2000 Бк. Период полураспада 11Na24 равен 15 часам. Каков объём крови человека, если через 3 часа удельная активность крови оказалась 0,445 Бк/см3.

5.37. При взрыве ядерного боеприпаса типа „деление" определенная доля ядер Pu239 не распадается. Она в дальнейшем дает α-распад и обуславливает основной фактор радиоактивного заражения местности. Подсчитать период полураспада изотопа Pu239, если постоянная распада равна 9,2 · 10-13 с-1. Сделать вывод об опасности подобного заражения.

5.38. При взрыве ядерного боеприпаса типа "деление", в основе которого лежит реакция распада изотопа U235, в почве под действием нейтронов образуется радиоактивный изотоп Na24, дающий электронный β-распад. Этот же изотоп образуется также и при взрыве нейтронного боеприпаса. Определить период полураспада Na24, если за 11 часов распалось 40 % от общего количества ядер. Сделать вывод об опасности заражения местности радиоактивным натрием.

5.39. За восемь суток распалось 75 % начального количества радиоактивного нуклида. Определить период полураспада.

5.40. Счетчик Гейгера, установленный вблизи препарата радиоактивного изотопа серебра, при первом измерении регистрировал 5200 β-частиц в минуту, а через сутки — только 1300. Определить период полураспада изотопа.

5.41. Образец радиоактивного радона Rn222 содержит 1010 радио­активных атомов. Сколько атомов распадается за сутки?

5.42. Подсчет сцинтилляции показывает, что в результате распада 1 г урана-235 выделяется примерно 1,23 · 104 а-частиц в секунду. Найти постоянную распада урана.

5.43. Сколько ядер распадается в 1 с в препарате радиоактивного иридия Ir192, если масса препарата равна 5 г? Какая часть начального количества иридия останется не распавшейся через один месяц? Период полураспада иридия 11,8 суток.

5.44. Определить среднее время жизни атомов радиоактивного изотопа, если известно, что число атомов данного изотопа уменьшается за 10 суток на 12,2 %.

5.45. Период полураспада изотопа Bi210 равен 4,97 дня. Какой активностью будет обладать 1 мг этого препарата, выдержанного в течение 10 дней?

5.46. В кровь человека ввели 1 см3 раствора, содержащего искусственный радиоизотоп натрия Na24 активностью 2 · 103 Бк. Активность 1 см3 крови, взятой через 5 часов, оказалось равной 16 распадам в минуту. Определить объем крови человека.

5.47. Определить величину слоя половинного ослабления радиоактивного излучения для следующих сред: дерево, грунт, бетон, танковая броня, свинец. Линейные коэффициенты ослабления излучения принять равными 2,8; 5,6; 7; 25; 75 м-1. Сделать выводы о применении указанных веществ для защиты от радиации.

5.48. Ядра ртути 80Hg190 имеют Т= 20 мин. Через сколько времени распадётся 90 % изотопа?

5.49. Через пять лет осталось 20 % ядер изотопа 11Na22. Чему равна постоянная радиоактивного распада? Каков период полураспада изотопа радиоактивного атома?

5.50. Из 2 · 106 ядер изотопа франция 87Fr207 через 50 с распалось 1,8 · 106 ядер. Найти среднее время жизни радиоактивного атома и период полураспада. Какая часть радиоактивных ядер останется через сутки?

5.51. Период полураспада ядер платины 78Pt200 равен 750 минут. Какая часть ядер распадется через час, через сутки? Чему равна будет при этом радиоактивность вещества?

5.52. При прохождении через слой вещества толщиной 1 см интенсивность моноэнергетического γ-излучения уменьшилась в 10 раз. Определить толщину слоя половинного поглощения и коэффициент ослабления этого вещества?

5.53. В качестве экрана от рентгеновского излучения используется пластина свинца толщиной 0,5 см. Его коэффициент поглощения равен 52,5 см-1. Какой толщины нужно взять пластину из алюминия, коэффициент поглощения которого 0,765 см-1, чтобы она экранировала в такой же степени?

5.54. Для защиты от у-лучей, энергия которых равна 4 МэВ, используется свинцовый экран толщиной 6 см. Какова должна быть толщина бетонного экрана, обеспечивающего ту же эффективность защиты?

5.55. Какова толщина слоя воды, который ослабляет поток γ-лучей с энергией 3,4 МэВ так же, как слой свинца толщиной 1 см?

5.56. Натрий 11Na23, облучаемый дейтронами, превращается в радиоактивный изотоп натрия 11Na24 с периодом полураспада Т = 15,5 ч. Какая доля первоначального количества радиоактивного натрия остаётся через сутки, если прекратить облучение дейтронами?

5.57. Радиоактивный изотоп углерода 6С14 в куске старого дерева составил 0,312 массы этого изотопа в живых растениях. Определить возраст куска дерева, если период полураспада изотопа углерода 6С14 равен 5570 годам.

5.58. Активность радиоактивного элемента уменьшилась за 100 суток в 16 раз. Каков период полураспада этого элемента?

5.59. Как изменится активность препарата кобальта в течение трех лет, если период его полураспада 5,2 года?

5.60. Вычислить удельную энергию связи ядра 7N14.

5.61. Определить мощность атомной электростанции, суточный расход U235 составляет 79 г, при КПД электростанции, равным 20 %, Энергию, выделяющуюся при одном акте деления, принять равной 200 МэВ.

5.62. Через пять лет осталось 20 % ядер изотопа 11Na22. Каковы период полураспада изотопа и среднее время жизни радиоактивного атома?

5.63. Рассчитать мощность атомной электростанции, работающей на обогащенном уране-235 с содержанием урана 25 кг/т, если за сутки расходуется 17 кг урановой руды при КПД 25 %. Принять, что при одном делении ядра урана выделяется 200 МэВ.

5.64. Мощность атомных установок подводной лодки, работающей на обогащенном уране-235 с 25%-ным содержанием радиоактивных ядер, равна 12 МВт. Определить максимально возможный срок плавания лодки при запасе горючего 18,6 кг.

5.65. Определить массу и радиоактивность полония 84Ро210 через один месяц, если его начальная радиоактивность равна 7 · 108 расп/с.

5.66. Каков объем крови человека, если при введении раствора с изотопом 11Na24 с активностью 2500 Бк и периодом полураспада 15 часов через два часа удельная активность крови стала равной 0,4 Бк/см3?

5.67. Для гашения γ-излучения используется вещество, уменьшающее интенсивность излучения в 20 раз на толщине 5 см. Каковы коэффициент ослабления вещества и толщина слоя половинного поглощения?

5.68. Определить объем крови человека, если введенная человеку жидкость объемом 1 см3 с; изотопом 11Na24 радиоактивностью 2 · 103 Бк, через 4 часа давала на 1 см3 крови 22 распада в минуту.

5.69. Коэффициент поглощения рентгеновского излучения свинца 52,3 см-1. Во сколько раз пластинка толщиною 0,2 см сильнее ослабляет интенсивность рентгеновских лучей, чем пластинка в десять раз тоньше? Чему равна толщина слоя половинного поглощения свинца для рентгеновского излучения?

5.70. Сравнить энергетический выход ядерных реакций синтеза ядер дейтерия и трития и реакций деления ядер урана-235 в расчете на один нуклон.

5.71. Период полураспада изотопа ртути 80Hg190 равен 20 минутам. Какая часть радиоактивных ядер ртути останется через один час?

5.72. Счетчик Гейгера при первом измерении радиоактивности изотопа зафиксировал 104 β-частиц в минуту. Через сутки число распадов уменьшилось на 7000. Определить период полураспада изотопа и постоянную его распада.