Закон электромагнитной индукции фарадея
2. Шар радиуса ![]() , равномерно заряженный с объемной плотностью заряда
, равномерно заряженный с объемной плотностью заряда ![]() , вращается вокруг своей оси симметрии с угловой скоростью
, вращается вокруг своей оси симметрии с угловой скоростью ![]() . Найдите векторный потенциал и напряженность магнитного поля внутри и снаружи шара.
. Найдите векторный потенциал и напряженность магнитного поля внутри и снаружи шара.
Дополнительный блок задач
3. Объемная плотность тока в пространстве меняется от точки к точке по периодическому закону 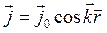 , где векторы
, где векторы ![]() и
и ![]() удовлетворяют соотношению
удовлетворяют соотношению 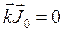 . Найдите векторный потенциал и напряженность магнитного поля, которые созданы этим током в неограниченном пространстве.
. Найдите векторный потенциал и напряженность магнитного поля, которые созданы этим током в неограниченном пространстве.
4. Объемная плотность тока в цилиндрических координатах имеет вид 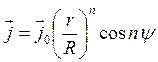 при
при ![]() и
и 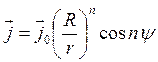 при
при ![]() , где постоянный вектор
, где постоянный вектор ![]() параллелен оси Z,
параллелен оси Z, ![]() – постоянная, а целое положительное число
– постоянная, а целое положительное число ![]() больше единицы. Найдите векторный потенциал
больше единицы. Найдите векторный потенциал ![]() магнитного поля в каждой точке пространства.
магнитного поля в каждой точке пространства.
Практическое занятие №10
Закон электромагнитной индукции Фарадея
Краткие теоретические сведения
М. Фарадей экспериментально открыл явление электромагнитной индукции, состоящее в возникновении электрического тока в замкнутом проводнике при изменении потока вектора магнитной индукции, охватываемого контуром. Позднее Э. Х. Ленц сформулировал правило, определяющее направление индукционного тока, математическую запись закона электромагнитной индукции с учетом правила Ленца предложил Ф. Э. Нейман –
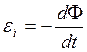 , ()
, ()
где ![]() – поток вектора магнитной индукции через площадь контура,
– поток вектора магнитной индукции через площадь контура,
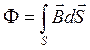 . ()
. ()
В дифференциальной форме математическая запись закона электромагнитной индукции представляет собой одно из уравнений Максвелла –
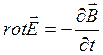 . ()
. ()
Замкнутый контур может создавать поток вектора магнитной индукции и за счет собственного тока. Соответственно, при изменении тока изменяется и поток, возникает индукционный ток. Это явление называется самоиндукцией. Учитывая связь магнитного потока с силой тока
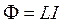 , ()
, ()
где ![]() – индуктивность контура, для явления самоиндукции получаем
– индуктивность контура, для явления самоиндукции получаем
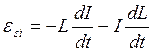 . ()
. ()
Темы для развернутых ответов
1. Закон электромагнитной индукции Фарадея.
2. Явление самоиндукции и его применение.
Литература: [1], глава 8, §45; [3], глава 6, §77.
Основной блок задач
1. По длинному проводнику течет ток ![]() . В магнитном поле этого тока находится квадратная проволочная рамка сопротивлением
. В магнитном поле этого тока находится квадратная проволочная рамка сопротивлением ![]() и стороной
и стороной ![]() . Центр рамки находится на расстоянии
. Центр рамки находится на расстоянии ![]() от проводника с током. Нормаль к плоскости рамки и вектор магнитной индукции составляют угол
от проводника с током. Нормаль к плоскости рамки и вектор магнитной индукции составляют угол ![]() . Какой заряд протечет в рамке за время изменения тока в проводнике от первоначального значения до 0? (Магнитным полем индукционного тока в рамке пренебречь.)
. Какой заряд протечет в рамке за время изменения тока в проводнике от первоначального значения до 0? (Магнитным полем индукционного тока в рамке пренебречь.)
2. В магнитном поле бесконечно длинного прямого проводника с током находится прямоугольная рамка, сделанная из металлической проволоки, со сторонами ![]() и
и ![]() , причем сторона
, причем сторона ![]() параллельна проводу с током. Ближайшая к проводу сторона рамки находится от него на расстоянии
параллельна проводу с током. Ближайшая к проводу сторона рамки находится от него на расстоянии ![]() . Определите среднее значение ЭДС индукции, возникающей в рамке, если ее удалять от проводника с током параллельно самой себе на расстояние
. Определите среднее значение ЭДС индукции, возникающей в рамке, если ее удалять от проводника с током параллельно самой себе на расстояние ![]() относительно первоначального положения со скоростью
относительно первоначального положения со скоростью ![]() .
.
3. В магнитном поле бесконечно длинного проводника с током ![]() со скоростью
со скоростью ![]() движется проводник длиной
движется проводник длиной ![]() по направлению, перпендикулярному току. Проводник во время движения остается параллельным току. Найдите ЭДС индукции в проводнике при любом законе движения? Каким должен быть закон движения проводника, чтобы ЭДС индукции оставалась постоянной?
по направлению, перпендикулярному току. Проводник во время движения остается параллельным току. Найдите ЭДС индукции в проводнике при любом законе движения? Каким должен быть закон движения проводника, чтобы ЭДС индукции оставалась постоянной?
Дополнительный блок задач
4. Индукция магнитного поля изменяется по закону 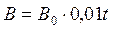 . Вектор магнитной индукции перпендикулярен площадке
. Вектор магнитной индукции перпендикулярен площадке ![]() , ограничивающей его магнитный поток. На расстоянии
, ограничивающей его магнитный поток. На расстоянии ![]() от центра площадки находится заряженная частица с зарядом
от центра площадки находится заряженная частица с зарядом ![]() и массой
и массой ![]() . Определите тангенциальное ускорение этой частицы.
. Определите тангенциальное ускорение этой частицы.


