Закон сохранения плотности энергии-импульса в дифференциальной форме

где – единичный вектор. Запишем выражение (3.12.1) в двухвекторном виде

Здесь 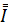– единичный вектор, а .

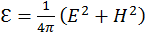Воспользуемся законом сохранения плотности энергии-импульса в дифференциальной форме, где µ=i ( = 1, 2, 3).

Т. к. ρ= 0, 1, 2, 3, то получим следующее выражение

Подставим выражения для плотности энергии-импульса в явном виде:

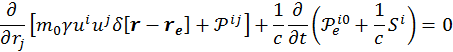
и возьмем интеграл по объему dV. С учетом того, что 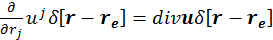, будем иметь

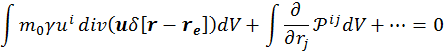
Используя теорему Остроградского – Гаусса, получим

Выберем замкнутую поверхность на большом удалении от системы (заряда), где δ-функция равна нулю. Применим теорему Остроградского – Гаусса:

Запишем импульс электромагнитного поля, создаваемого зарядами данной системы:

Полное изменение импульса в системе в единицу времени равно потоку импульса через замкнутую поверхность с обратным знаком:

где – это вектор, направленный по нормали к поверхности наружу; 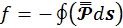— пондеромоторная сила, действующая на замкнутую систему. При этом в зависимости от ситуации эта сила может быть направлена либо внутрь системы, либо наружу.

В качестве самостоятельной работы, предлагается два упражнения.

Упражнение 1. Найти силу давления магнитного поля на поверхность цилиндрического проводника с током.

Упражнение 2. Найти силу давления света в фокусе лазера терраватной мощности 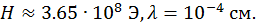Ответ выразить в килограммах.

Таблица напряженностей магнитного поля.

*СКВИД-SQID-Superconductive Quantum Interference Device.

§ 3.13. Закон сохранения плотности энергии-импульса в дифференциальной форме. Сила Лоренца.

Мы уже знаем, что плотность силы в теории поля определяется следующим образом:

Но эту же величину можно записать как

Следовательно, получаем закон:

Эта формула является законом сохранения энергии-импульса в дифференциальной форме.

Покажем теперь, что из этого закона можно получить силу, которая действует на заряд в электромагнитном поле – силу Лоренца. Распишем плотность силы для частицы согласно (3.9.5) на номера:

и согласно (3.10.6)

Подставим сюда четырехмерный вектор плотности тока в интегральной форме (3.7.8) в выражение для плотности силы для поля:

Теперь можно записать закон сохранения в виде

Нулю равно выражение в фигурных скобках, так как дельта-функция не является тождественно равной нулю. Таким образом, можно записать, что

Правая часть уравнения (3.13.7) и есть сила Лоренца.

Глава IV

ТЕОРИЯ ЧАСТИЦ И ПОЛЕЙ

§ 4.1. Об устойчивости статической системы электрических зарядов. Теорема Ирншоу

Устойчивости статической системы зарядов в принципе в природе не существует, поэтому наш параграф называется об устойчивости. Возникает вопрос: можно ли, подбирая знаки и величины зарядов, создать устойчивую систему? Ответ: можно. Придумаем такую систему.

Такая система может быть устойчивой. Здесь положительные заряды отталкиваются друг от друга, но будет существовать и сила притяжения между положительными и отрицательными зарядами, которая будет равна по величине силе отталкивания.