Законы ома и джоуля — ленца

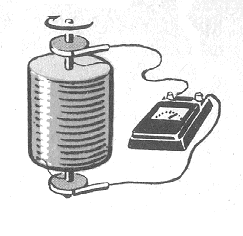
Схема этих опытов такова. На катушку наматывают проволоку, концы которой припаивают к двум металлическим дискам, изолированным друг от друга (рис. 8.4). К концам дисков при помощи скользящих контактов присоединяют гальванометр.

Катушку приводят в быстрое вращение, а затем резко останавливают. После резкой остановки катушки свободные заряженные частицы будут некоторое время двигаться относительно проводника по инерции, и, следовательно, в катушке возникнет электрический ток. Ток будет существовать незначительное время, так как из-за сопротивления проводника заряженные частицы тормозятся и упорядоченное движение частиц, образующее ток, прекращается.

Наблюдения показали, что в цепи после остановки катушки некоторое время существует ток. Направление его говорит о том, что он создается движением отрицательно заряженных частиц. Переносимый при этом заряд пропорционален отношению заряда частиц, создающих ток, к их массе, т. е. 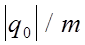. Поэтому, измеряя заряд, проходящий через гальванометр за все время существования тока в цепи, удалось определить отношение 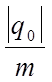. Оно оказалось равным 1,8 × 1011 Кл/кг. Эта величина совпадает с отношением заряда электрона к его массе e/m, найденным ранее из других опытов.

8.4. Законы Ома и Джоуля — Ленца в дифференциальной форме

При прохождении электрического тока по проводнику совершается работа A=qU, которая по закону сохранения и превращения энергии идет на нагревание проводника. Если ток постоянный, то q=It, тогда

A=UIt (8.7)

Это математическое представление закона Джоуля — Ленца.

Мощность, выделяемая в цепи, равна:

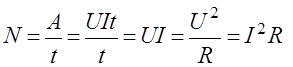. (8.8)

Выделим в веществе элементарный отрезок и применим к нему закон Ома для участка цепи:

.

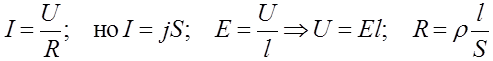Подставив данные выражения в формулу закона Ома, получим:

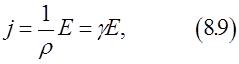
где 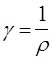– удельная проводимость проводника.

В векторной форме

Это и есть запись закона Ома в дифференциальной форме. Итак, плотность тока прямо пропорциональна напряженности электрического поля.

Получим закон Джоуля — Ленца в дифференциальной форме:

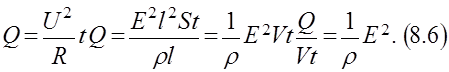
По определению, мощность тока:

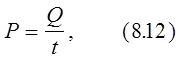
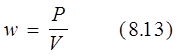
– объемная плотность мощности. Тогда закон Джоуля — Ленца в дифференциальной форме запишется :

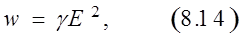
т. е. объемная плотность мощности тока прямо пропорциональна квадрату напряженности электрического поля.

Сверхпроводники 1-го и 2-го рода.

По своему поведению в магнитных полях сверхпроводники разделяются на сверхпроводники 1-го и 2-го рода. Сверхпроводники 1-го рода обнаруживают те идеальные свойства, о которых уже говорилось. В присутствии магнитного поля в поверхностном слое сверхпроводника возникают токи, которые полностью компенсируют внешнее поле в толще образца. Если сверхпроводник имеет форму длинного цилиндра и находится в поле, параллельном его оси, то глубина проникновения может быть порядка 3*10–6 см. При достижении критического поля сверхпроводимость исчезает, и поле полностью проникает внутрь материала. Критические поля для сверхпроводников 1-го рода лежат обычно в пределах от 100 до 800 Тл. Хотя у сверхпроводников 1-го рода малая глубина прони