Автоколебательные системы томпсоновского типа
Рис. 40. Вид фазовых траекторий для систем промежуточного типа.
Рис. 41. Вид фазовых траекторий для систем релаксационного типа.
Если мы построим на фазовой плоскости фазовые траектории для системы, у которой функция f(y) меняется в больших пределах (|f(y)| >> 1), то получим для данного вида f(y) фазовый портрет, показанный на рис. 41. Нелинейная функция f(y) такого вида соответствует автоколебательной системе релаксационного типа. Установление стационарных колебаний в подобных системах происходит практически за доли периода колебаний.
В общем случае для всех трёх систем процесс можно описать с помощью уравнения Ван дер Поля
|
|
(6.6) |
Здесь, естественно, f(x, y) = — e(1 — x2)y. В томпсоновской системе e ~ 0.1, в промежуточной e ~ 1, в релаксационной e ~ 10.
6.2. Автоколебательные системы томпсоновского типа
Уже было отмечено, что для автоколебательных систем томпсоновского типа характерны малая нелинейность и малое затухание за период колебаний. Это системы осцилляторного типа, и колебания в таких системах почти гармонические.
|
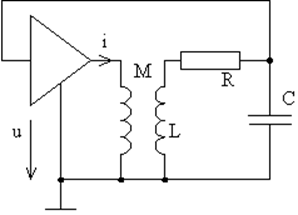
Рис. 42. Схема генератора с контуром в цепи управляющего напряжения. |
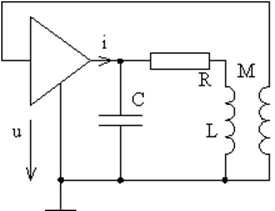
Рис. 43. Схема генератора с контуром в цепи управляемого тока. |
Рассмотрим автоколебательные системы с цепью обратной связи. В подобных системах накопителем энергии служит достаточно добротный колебательный контур, а вложение энергии, компенсирующее потери и полезный отбор энергии, осуществляется с помощью активного элемента и цепи обратной связи. В качестве активного элемента в электрических автоколебательных системах чаще всего используют полевые транзисторы, большое входное сопротивление которых не ухудшает добротность колебательного контура. При этом возможны два варианта автогенераторов: с колебательным контуром в цепи управляющего напряжения (рис. 42) и с колебательным контуром в цепи управляемого тока (рис. 43). Активный элемент на этих схемах показан треугольником.
Для генератора с колебательным контуром в цепи управляемого тока (рис. 43) можно записать закон Кирхгофа
|
|
(6.7) |
Пусть в качестве нелинейного элемента используется полевой транзистор, линейная характеристика которого описывается уравнением i = iС0 + Su, где iС0 — начальный ток стока, S — крутизна характеристики. Очевидно, что u = q/C = q0x/C, где q0 — амплитуда заряда на конденсаторе, тогда уравнение (6.7) запишется следующим образом:
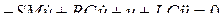 .
.
В нормированных координатах:
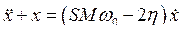 ,
,
где 2h = R/(w0L), t = w0t, 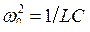 . Если SMw0 > 2h, то в системе будет нарастающий колебательный процесс; если SMw0 < 2h, то амплитуда колебаний будет уменьшаться, т. е. режим стабильной амплитуды практически недостижим.
. Если SMw0 > 2h, то в системе будет нарастающий колебательный процесс; если SMw0 < 2h, то амплитуда колебаний будет уменьшаться, т. е. режим стабильной амплитуды практически недостижим.
Нужно отметить, что при сделанных предположениях самовозбуждающиеся колебания в исследуемых системах нарастают неограниченно, чего не происходит в реальных системах. Это связано с тем, что принятая нами линейная аппроксимация ВАХ активного элемента пригодна лишь для небольших пределов изменения x. Это означает также, что при линейной характеристике невозможно получение стационарных автоколебаний и при их описании с помощью фазовой плоскости мы не будем иметь замкнутой фазовой траектории — предельного цикла.
В реальных генераторах выход на стабильную амплитуду достигается за счёт нелинейности усилителя или цепи обратной связи. В рассмотрении автоколебательных систем при нелинейных ВАХ метод комплексных амплитуд не работает, но работает метод гармонического баланса. Воспользуемся разновидностью МГБ — методом колебательных характеристик (МКХ). В этом методе вводится усреднённая крутизна нелинейной характеристики, которая является переменной величиной, зависящей от амплитуды колебаний управляющего напряжения. Будем считать, что цепь обратной связи — высокодобротный колебательный контур. Для такого колебательного контура можно считать напряжение на усилителе синусоидальным, тогда u(t) = Ucos(w0t), где w0 — собственная частота колебательного контура. Ток на выходе нелинейного усилителя будет периодической функцией времени, и эту функцию можно разложить в ряд Фурье
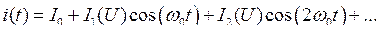
В рамках гармонического баланса, благодаря высокой добротности колебательного контура, можно ограничиться только основной гармоникой ряда. Введём колебательную характеристику элемента
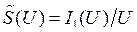 .
.
Тогда зависимость выходного тока усилителя от амплитуды напряжения на его входе принимает вид, аналогичный характеристике полевого транзистора:
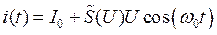 .
.
Это уравнение подставим в (6.7), откуда для стационарного режима получаем:
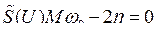 ,
,
а отсюда находим ![]() :
:
|
|
(6.8) |
В зависимости от выбора рабочей точки колебательная характеристика может быть как монотонной, так и не монотонной.
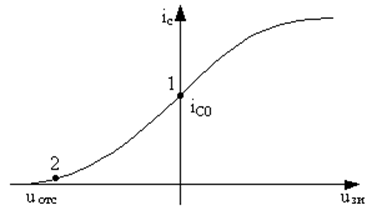
В качестве примера рассмотрим случай, когда активным элементом является МОП-транзистор с встроенным каналом. На рис. 44 показана нелинейная характеристика такого транзистора: iс = j(uзи).
|
Рис. 44. Характеристика зависимости тока стока iс от напряжения uзи на затворе МОП-транзистора. |
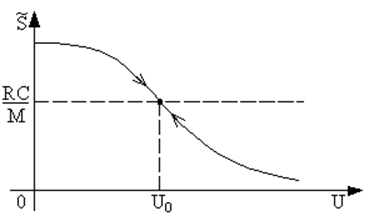
Рис. 45. Кривая средней крутизны для случая, когда рабочая точка соответствует максимальной крутизне. |
Для рабочей точки 1 вблизи начального тока стока колебательная характеристика является монотонной (рис. 45). В этом случае находим единственное решение — стационарную амплитуду колебаний U0, при которой в системе обеспечивается баланс вкладываемой и рассеиваемой энергии за период колебаний. Из того же рисунка следует, что полученное решение U0 не только единственно возможно, но и устойчиво. Действительно, если амплитуда колебаний U станет больше U0, то потери в системе, пропорциональные RC/M, будут превышать вложение энергии, пропорциональное ![]() , и амплитуда U вернётся в точку U0. И наоборот, если U станет меньше U0, то вложение энергии будет превосходить потери и, как следствие, амплитуда колебаний снова увеличится до значения U0.
, и амплитуда U вернётся в точку U0. И наоборот, если U станет меньше U0, то вложение энергии будет превосходить потери и, как следствие, амплитуда колебаний снова увеличится до значения U0.
Таким образом, фазовые траектории для такого случая будут выглядеть как показано на рис. 46 (когда 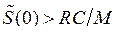 ) и рис. 47 (когда
) и рис. 47 (когда 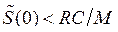 ). Такой режим возбуждения с выходом на предельный цикл называется мягким.
). Такой режим возбуждения с выходом на предельный цикл называется мягким.
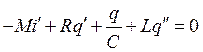 .
.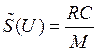 .
.