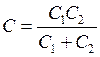Автономные системы, символические уравнения
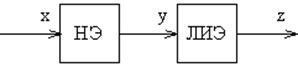
Введём проходное сопротивление:
|
|
(1.12) |
Высший порядок уравнения равен удвоенному числу обобщённых переменных, т. е. удвоенному числу степеней свободы. Этот пример мы рассматривали операторным методом, который применим только к линейным системам.
1.3. Автономные системы, символические уравнения Вопрос 2
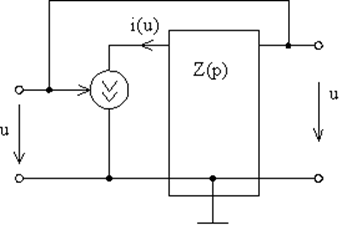
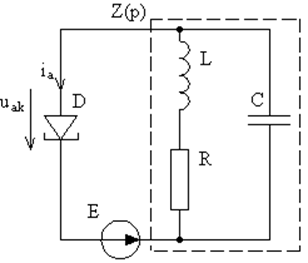
Общей теории нелинейных систем нет, поэтому рассматривают частные случаи, например, если система содержит безынерциальный нелинейный элемент и линейную инерциальную подсистему. На рис. 7 показана такая система, для которой
|
Рис. 7. |
где f — некоторая функция, |
Для анализа этой системы (для составления описывающего её уравнения) можно воспользоваться методом символических уравнений. Для этого формально записываются законы Кирхгофа в операторной форме, но вместо изображений токов и напряжений по Лапласу записываются их линейные значения, причём линейные элементы описываются операторным сопротивлением, а нелинейные — своей ВАХ. Полученные уравнения рассматриваются как алгебраические относительно p и преобразовываются так, чтобы p не было в знаменателе; после p заменяется оператором дифференцирования, т. е. ![]() .
.
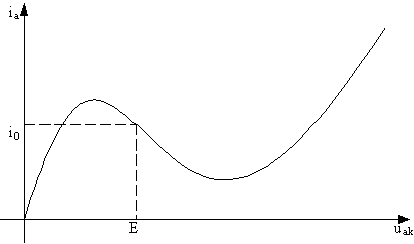
Применим это правило к генератору на туннельном диоде (рис. 8). Чтобы пошла генерация, необходимо рабочую точку вынести в область отрицательного дифференциального сопротивления (как показано на рис. 9).
|
Рис. 8. Генератор на туннельном диоде. |
Рис. 9. ВАХ туннельного диода. |
Будем действовать по правилу, составим формальное уравнение:
![]() .
.
Найдём операторное сопротивление контура (линейной инерциальной подсистемы), обведённого штриховой линией на рис. 8: здесь последовательное соединение индуктивности и сопротивления в параллель с конденсатором, т. е.
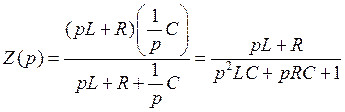 .
.
Введём другие обобщённые координаты (относительно рабочей точки):
![]() ,
,
тогда можно записать:
|
|
(1.13) |
Символическое уравнение цепи в общем случае имеет вид:
|
|
(1.14) |
т. е. полученное уравнение (1.13) удовлетворяет условию (1.14). Дальше получаем ДУ:
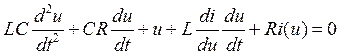 ;
;
причём, так как генератор будет работать в области выбранной нами рабочей точки, то можно приблизительно заменить i(u) на i0, тогда
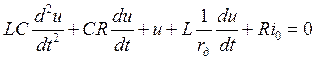 .
.
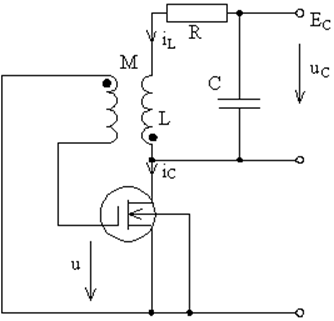
Рассмотрим генератор на транзисторе, представленный на рис. 10. Линейной подсистемой в
|
Рис. 10. Генератор на транзисторе. |
этом генераторе является резонансный контур. Запишем несколько соотношений, которые легко получаются, если немного приглядеться к схеме:
и сведём их к одному уравнению:
Из последнего уравнения следует равенство: |
|
|
(1.15) |
|
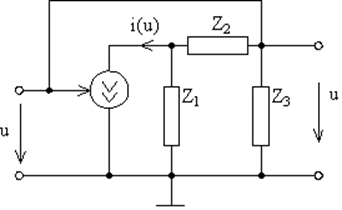
Как видно, уравнения (1.15) и (1.13) похожи — это один из примеров изоморфизма колебательных систем, поэтому можно зарисовать обобщённую структуру генератора (рис. 11). Часто вместо Z(p) используют так |
называемую трёхточечную схему (рис. 12). В этом случае общее уравнение генератора на управляемом источнике, охваченного обратной связью через линейный четырёхполюсник (рис. 11) имеет вид:
|
|
(1.16) |
где (для трёхточечной схемы) операторное сопротивление:
|
|
(1.17) |
В качестве примеров рассмотрим генератор с автотрансформаторной связью (рис. 13) и схему Колпитца (рис. 14). Подставив соответствующие Z1(p), Z2(p) и Z3(p) в уравнение (1.17) получим следующие операторные сопротивления:
|
|
(1.18) |
для генератора с автотрансформаторной связью (индуктивной трёхточки);
|
|
(1.19) |
для схемы Колпитца (емкостной трёхточки).
|
Рис. 11. Общая структура генератора. |
Рис. 12. Трёхточечная схема. |
Подставляя (1.18) и (1.19) в уравнение (1.16), получим ДУ, описывающие колебательные процессы в индуктивной трёхточке:
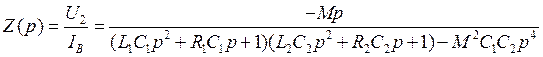 .
.
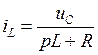 ,
, 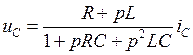 ;
;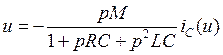 .
.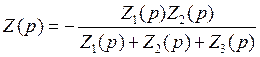 .
.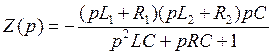 , где
, где 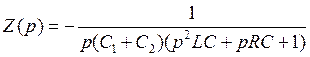 , где
, где