Четырехмерное пространство и четырехмерная символика

3)  Скорость любой материальной частицы не может превышать скорость света.

Этот факт находит убедительное подтверждение. Предположим противное. Тогда мы можем передавать взаимодействия между такими частицами со скоростями большими скорости света. А это противоречит постулату Эйнштейна.

СТО является основой новой механики, отличной от механики Ньютона. Она называется релятивистской механикой, а частицы, которые летят со скоростью, близкой к скорости света, называются релятивистскими частицами.

Как сопоставить законы релятивистской механики с законами механики Ньютона?!

Релятивистская механика является обобщением механики Ньютона на случай движения частиц с релятивистскими скоростями. Поэтому, если скорость частицы U<<c, то можно пользоваться механикой Ньютона.

В макроскопической физике действует механика Ньютона, а в микрофизике – релятивистская механика. Эта ситуация отражает принцип соответствия в физике (всякая новая теория в каких-то областях должна совпадать с хорошо известной и проверенной теорией).

§ 1.2. Четырехмерное пространство и четырехмерная символика

Поскольку время в специальной теории относительности не является абсолютным, то его можно рассматривать как четвертую координату, наравне с другими пространственными координатами. Образованное таким образом четырехмерное пространство будем считать однородным и изотропным, также как и обычное пространство в ньютоновской физике. Все оси четырехмерного пространства будем считать взаимно перпендикулярными. Координаты точки в четырехмерном пространстве образуют совокупность четырех величин:

rµ=(x, y, z, kt) (µ=1, 2, 3, 4), (1.2.1)

где k-некоторый произвольный размерный множитель. Размерность этого множителя должна равняться [см/с], чтобы все компоненты rµ имели размерность длины.

Определяемая таким образом величина rµ является по существу четырехмерным вектором, у которого начало совпадает с началом координат, а конец попадает в точку с координатами (x, y, z. kt). Эта точка называется мировой точкой. Если частица движется, то ее мировая точка тоже будет перемещаться, но в четырехмерном пространстве. Такая кривая называется мировой линией. Расстояние между двумя мировыми точками в четырехмерном пространстве называется интервалом и аналогично трехмерному

пространству определяется выражением: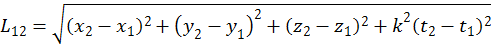
(1.2.2)

Эта формула является аналогом расстояния между двумя точками в трехмерном пространстве. Ее можно переписать короче:

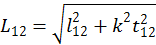(1.2.3)

В частном случае, когда одна мировая точка находится в начале координат, то можно принять, что r1=0, а r2=r:

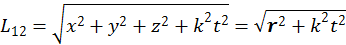(1.2.4)

Расстояние между двумя точками в четырехмерном пространстве не должно зависеть от выбора той или иной инерциальной системы координат. Это означает, что интервал является инвариантной величиной.

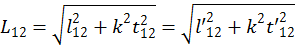(1.2.5)

В таком случае отсюда вытекает, что

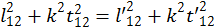(1.2.6)

Здесь могут реализоваться две ситуации.

1.  Если время является абсолютным, то

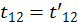(1.2.7)

Тогда и 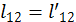, т. к. k=сonst.

Как и должно быть, в трехмерном пространстве расстояние между точками является инвариантом, т. е. мы находимся в рамках ньютоновской физики.

2.  Если время не является абсолютным, то

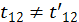(1.2.8)

Чтобы интервал оставался инвариантом надо потребовать, чтобы 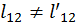, но тогда в трехмерном пространстве расстояние между точками может изменяться при переходе от одной инерциальной системы отсчета к другой.

Определим коэффициент k из условия инвариантности интервала в четырехмерном пространстве.

Рассмотрим две инерциальные системы отсчета.

Из точки 1 с координатами (x1,y1,z1,kt1) испускается луч света, который попадает в точку 2 с координатами (x2, y2, z2, kt2)(рис.4). Можно сказать, что

Условие инвариантности интервала для этого эксперимента:

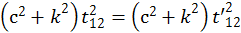, (1.2.9)

причем 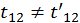. Тогда левая часть будет равна правой только в том случае, когда 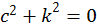. Отсюда следует, что 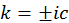, где 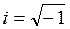— мнимая единица.

Таким образом, мы получили компоненты четырехмерного вектора

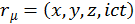(1.2.10)

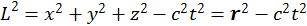(1.2.11)

Так как все координаты равноправны, то

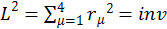(1.2.12)

Обычно принято считать время действительной величиной, но для того, чтобы интервал имел тот же самый вид, удаление мнимой единицы производится путем введения двух типов координат: ковариантных координат(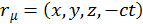) и контравариантных().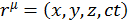