Четырехмерный вектор плотности силы
![]()
Здесь
![]()
— скорость заряда в данной точке пространства, т. е. скорость данного точечного заряда с радиус-вектором ![]() ;
; ![]() — плотность заряда, которая зависит от произвольной точки.
— плотность заряда, которая зависит от произвольной точки.
Мы вводим понятие плотности тока в теории поля, чтобы исключить из рассмотрения точечные заряды (т. к. в теории поля заряд непрерывный, “размазанный”). Плотность точечного заряда в теории поля равна
![]()
где 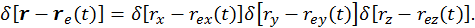
Мы знаем, что δ-функция нормирована на единицу:

Следовательно, плотность заряда, проинтегрированная по всему пространству, даст нам сам заряд.
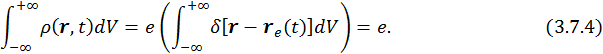
Трехмерный вектор плотности тока записывается следующим образом:
![]()
![]()
Скорость заряда ![]() – не зависит от координат, следовательно, ее можно вынести за знак интеграла. Объединяя полученные формулы, получим:
– не зависит от координат, следовательно, ее можно вынести за знак интеграла. Объединяя полученные формулы, получим:
![]()
Здесь 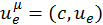 – не четырехмерный вектор скорости, но нековариантность
– не четырехмерный вектор скорости, но нековариантность ![]() компенсируется нековариантностью плотности заряда, так что в целом
компенсируется нековариантностью плотности заряда, так что в целом 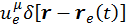 — это четырехмерный вектор, поэтому
— это четырехмерный вектор, поэтому 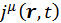 также является четырехмерным вектором.
также является четырехмерным вектором.
Проверим размерность:
![]()
Можно ввести четырехмерный вектор плотности тока в явно ковариантной форме.
![]()
где ![]() — четырехмерный вектор скорости точечного заряда в точке с четырехмерным радиус-вектором
— четырехмерный вектор скорости точечного заряда в точке с четырехмерным радиус-вектором ![]() ;
; ![]() — инвариантный параметр, имеет размерность времени, после интегрирования перейдет в собственное время.
— инвариантный параметр, имеет размерность времени, после интегрирования перейдет в собственное время.
![]()
По свойству δ-функции имеем:
![]()
Надо проверить, что плотность тока в явной ковариантной форме дает те же компоненты, что были записаны ранее.
![]()
Используя формулу

снимем интегрирование по ![]() . Здесь
. Здесь ![]() – корень уравнения
– корень уравнения 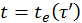 ;
; ![]() – время наблюдателя, но при
– время наблюдателя, но при 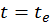 оно совпадает с собственным временем точечной частицы.
оно совпадает с собственным временем точечной частицы.
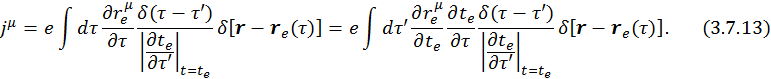
Введем гамма-фактор
![]()
При подстановке в (3.7.13) получим
![]()
Четырехмерный вектор плотности тока должен удовлетворять уравнению непрерывности плотности тока:
![]()
Убедимся в его выполнении для данного вектора плотности тока ![]() :
:
![]()
Внесем производную под интеграл, тогда она будет действовать на δ-функцию.
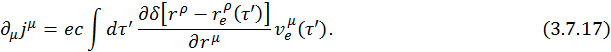
Воспользуемся правилом переброса производной от δ-функции. Перебросим производную от ![]() к
к ![]() , тогда получим
, тогда получим
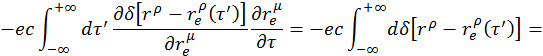
![]()
так как δ-функция на бесконечности равна нулю, следовательно, уравнение непрерывности выполняется.
§ 3.8. Четырехмерный вектор плотности силы
В теории поля вместо четырехмерного вектора силы ![]() вводится четырехмерный вектор плотности силы
вводится четырехмерный вектор плотности силы ![]() .
.
Рассмотрим, как вводится этот вектор на примере силы Лоренца, действующей на заряд во внешнем поле:
![]()
Если теперь поделить обе части на гамма-фактор, то будем иметь
![]()
где согласно (3.7.6) и (3.7.7) 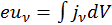 , а значит
, а значит
![]()


