Закон полного тока в вакууме
При конечном перемещении проводника с током, имеющего конечные размеры, выражения работы силы Ампера через заметённый магнитный поток и, соответственно, через изменение потокосцепления имеют вид:
![]()
§20.3. Закон полного тока (теорема Стокса) в вакууме
Как известно, электростатическое поле потенциально, поскольку циркуляция напряжённости электростатического поля по произвольному замкнутому контуру L
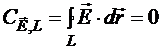 .
.
Вопрос с циркуляцией ![]() в вакууме будем решать на примере поля, созданного бесконечным прямым проводником с током, а потом бездоказательно обобщим на произвольное магнитное поле.
в вакууме будем решать на примере поля, созданного бесконечным прямым проводником с током, а потом бездоказательно обобщим на произвольное магнитное поле.
Сначала в качестве замкнутого контура L возьмём силовую линию, отстоящую от тока на расстояние r.
 Рис.20.4
Рис.20.4
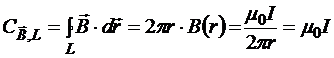
Теперь рассмотрим произвольный контур, охватывающий ток.
 Рис.20.5
Рис.20.5
Поскольку вектор ![]() в любой точке контура направлен по касательной к концентричной току окружности, то составляющая элемента контура
в любой точке контура направлен по касательной к концентричной току окружности, то составляющая элемента контура ![]() , сонаправленная с
, сонаправленная с ![]() ,
, ![]() . Тогда
. Тогда
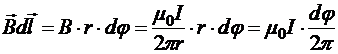 .
.
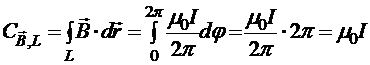 .
.
Договоримся, что если направление тока в проводнике согласуется с направлением обхода контура по правилу правого винта, то для данного контура ток положителен, а если нет, то отрицателен.
Предположим, что замкнутый контур не охватывает проводник с током.
 Рис.20.6
Рис.20.6
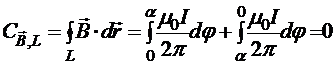
Обобщим полученные результаты на произвольную конфигурацию тока и запишем общее правило: циркуляция вектора ![]() по любому контуру, охватывающему проводник с током, равна произведению магнитной постоянной вакуума на силу тока, снабжённому знаком в соответствие с правилом правого винта.
по любому контуру, охватывающему проводник с током, равна произведению магнитной постоянной вакуума на силу тока, снабжённому знаком в соответствие с правилом правого винта.
В случае, если магнитное поле создаётся несколькими проводниками с током, то общее поле находится в соответствие с принципом суперпозиции, следовательно,
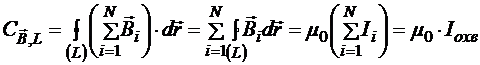
Таким образом, мы получаем закон полного тока:
![]() ,
,
где охваченный контуром полный ток ![]() равен алгебраической сумме токов, пронизывающих поверхность, натянутую на этот контур.
равен алгебраической сумме токов, пронизывающих поверхность, натянутую на этот контур.
В случае непрерывного распределения вектора плотности тока по плоскости контура закон полного тока называется теоремой Стокса:
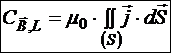
Циркуляция вектора магнитной индукции по данному контуру равна потоку вектора плотности тока через поверхность, натянутую на контур и ориентированную по направлению обхода контура в соответствие с правилом правого винта.
§20.4. Поле тороида
На основании закона полного тока выведем формулы, магнитного поля тороида и длинного соленоида.
Тороид — это кольцевая катушка с током, витки которой равномерно намотаны на сердечник, имеющий форму тора.
Если витки катушки расположены вплотную, то тороид можно приближённо рассматривать как систему большого числа плотно уложенных одинаковых витков с токами, идущими в одном направлении.
 Рис.20.7
Рис.20.7
Центры витков лежат на центральной линии тора (на рисунке 20.7 показана пунктиром) и имеют радиус (R2-R1)/2.
Из соображений цилиндрической симметрии относительно оси тора понятно, что магнитные силовые линии представляют собой концентрические окружности, центры которых лежат на оси тора. Тогда для контура, совпадающего с силовой линией радиуса r, циркуляция ![]() . При r<R1 поверхность, натянутую на контур, не пересекает ни один проводник с током, следовательно
. При r<R1 поверхность, натянутую на контур, не пересекает ни один проводник с током, следовательно ![]() =0 и В=0. При r>R2 поверхность, натянутую на контур, каждый виток пересекает дважды: один раз в положительном, другой раз в отрицательном направлениях, следовательно,
=0 и В=0. При r>R2 поверхность, натянутую на контур, каждый виток пересекает дважды: один раз в положительном, другой раз в отрицательном направлениях, следовательно, ![]() и В тоже равны 0. Поэтому поле тороида локализовано внутри него. Для R1<r< R2
и В тоже равны 0. Поэтому поле тороида локализовано внутри него. Для R1<r< R2 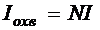 , где N — число витков тороида. Тогда
, где N — число витков тороида. Тогда 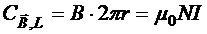 , следовательно,
, следовательно,
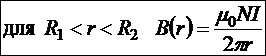
Тонким называется тороид, радиус витков которого значительно меньше радиуса средней линии 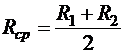 . Тогда любой радиус R1<r< R2 будет примерно равен Rcp. И в этом случае поле внутри тороида можно считать однородным по поперечному сечению тора. Тогда
. Тогда любой радиус R1<r< R2 будет примерно равен Rcp. И в этом случае поле внутри тороида можно считать однородным по поперечному сечению тора. Тогда
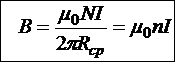 ,
,
где плотность витков намотки .
Бесконечный соленоид — бесконечная стопа из витков с одинаковым током одинаковой формы (окружность) и размера. Технически реализуется как плотно намотанная спираль из изолированного провода, поперечное сечение которой значительно меньше её длины. Очевидно, что бесконечный соленоид можно рассматривать как тороид с бесконечными R2 и R1. Тогда — это тонкий тороид. Следовательно, за пределами длинного соленоида поля нет, а внутри него оно однородно и описывается приведёнными выше формулами (l – длина соленоида):
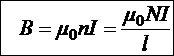 .
.
Контрольные вопросы к главе 20
1. К источнику тока с ЭДС, равной 0,5 В и ничтожно малым внутренним сопротивлением присоединены два металлических стержня, расположенные горизонтально и параллельные друг другую Расстояние между стержнями равно 20 см. Стержни находятся в однородном магнитном поле, направленном вертикально. Магнитная индукция равна 1,5 Тл. По стержням под действием сил поля скользит со скоростью 1 м/с прямолинейный проводник, сопротивление которого равно 0,02 Ом. Сопротивление стержней пренебрежимо мало. Чему равна ЭДС, действующая в проводнике? (Ответ: 0,3 В) (§ 20.2)
2. Чему равна сила, действующая на скользящий проводник из первой задачи? (Ответ: 3 Н) (§ 20.2)
3.Чему равна сила тока в цепи, замкнутой сколзящим проводником из первой задачи? (Ответ: 10 А) (§ 20.2)
4. Чему равна механическая мощность, расходуемая на движение проводник из первой задачи? (Ответ:3 Вт ) (§ 20.2)
5. Чему равна мощность источника тока из первой задачи? (Ответ: 5 Вт) (§ 20.2)
6. Чему равна тепловая мощность, выделяемая в скользящем проводнике из первой задачи? (Ответ: 2 Вт) (§ 20.2)
7. Два одинаковых пропеллера с узкими металлическими лопастями вращаются с частотой 50 Гц в магнитном поле, перпендикулярном плоскостям вращения, в противоположных направлениях. Магнитная индукция равна 10 Тл, каждый пропеллер имеет две лопасти длиной 0,5 м. Чему равна разность потенциалов между центрами пропеллеров? (Ответ: 250 В) (§ 20.2)
8. По кольцу, сделанному из гибкого провода радиусом 10 см, течёт ток, сила которого равна 100 А. Перпендикулярно плоскости кольца возбуждено магнитное поле с индукцией 0,1 Тл по направлению, противоположному магнитному моменту кольца. Чему равна работа внешних сил, которые, действуя на провод, деформировали его и придали форму квадрата? Сила тока и ориентация плоскости контура поддерживались неизменными (Ответ: -67,5 мДж) (§ 20.2)


