Понятие потенциала
то есть мы видим, что в рассматриваемом случае это действительно так (вектор ![]() отсчитывается от источника).
отсчитывается от источника).
Мы так подробно обсуждаю центральность поля точечного заряда, потому что центральное поле обладает замечательным свойством: оно потенциально. Определение потенциальности в отношении силового поля давалось в механике, там где шла речь о потенциальной энергии. Сейчас, опираясь на уже полученные знания, нам будет легко обобщить понятие потенциальности на любые (не обязательно силовые) векторные поля.
Определение: контурный интеграл векторного поля по замкнутому контуру L:
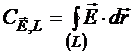
называется циркуляцией. Форма контура значения не имеет.
Потенциальным называется векторное поле, циркуляция которого по любому замкнутому контуру равна 0.
Легко доказать (уже доказывалось в лекциях по механике), что центральное поле обладает этим свойством.
следовательно,
Для дальнейшего важно понимать, что циркуляция не зависит от начала отсчёта. То есть если начало отсчёта векторов положения сместить из центра поля, циркуляция по данному замкнутому контуру по-прежнему будет равна 0. Это обстоятельство позволяет доказать, что электростатическое поле произвольной системы зарядов потенциально. Если поле создано не одним точечным зарядом, то согласно принципу суперпозиции
,
поскольку мы получили сумму циркуляций, каждая из которых равна 0. Начало отсчёта векторов положения произвольно (может находиться за пределами расположения системы зарядов).
§14.2. Понятие потенциала
Если векторное поле — силовое, то физический смысл скалярного произведения ![]() — элементарная работа dА силового поля на перемещении
— элементарная работа dА силового поля на перемещении ![]() материальной точки, чьё силовое поле мы рассматриваем. В механике доказывалось, то работа потенциального силового поля на перемещении
материальной точки, чьё силовое поле мы рассматриваем. В механике доказывалось, то работа потенциального силового поля на перемещении ![]() (рис.14.2)
(рис.14.2)
 Рис.14.2
Рис.14.2
выражается через сброс энергии положения или потенциальной энергии материальной точки в её силовом поле:
![]() .
.
Как Вы помните, потенциальная энергия определялась через отрицательную работу сил поля от некой точки пространства O, произвольно избранной в качестве начала отсчёта потенциальной энергии (W(О)=0).
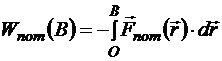 ,
,
где В — произвольная точка пространства, заполненного полем. При этом контур L, по которому материальная точка движется в потенциальном поле от точки О до точки В (то есть по которому производится интегрирование), может быть любым. В механике потенциальную энергию, как и любую другую энергию, принято обозначать буквой Е. В электромагнетизме энергия обозначается буквой W, поскольку Е «занята» на обозначении электрической напряжённости.
В случае поля электростатических сил, то есть сил, действующих со стороны зарядов-источников на пробный заряд q, его потенциальная энергия в этом поле
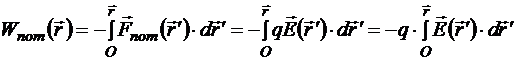
Дадим определение: потенциал ![]() в данной точке пространства
в данной точке пространства ![]() , заполненного электростатическим полем, совпадает с потенциальной энергией
, заполненного электростатическим полем, совпадает с потенциальной энергией ![]() , которую имел бы в этом поле точечный единичный положительный пробный заряд, если его поместить в данную точку. «Идеология» этого определения та же, что и в определении напряжённости. То есть слово «совпадает» связано с тем, что потенциал − это характеристика поля самого по себе, а потенциальная энергия пробного заряда в поле характеризует и поле, и пробный заряд. Иными словами,
, которую имел бы в этом поле точечный единичный положительный пробный заряд, если его поместить в данную точку. «Идеология» этого определения та же, что и в определении напряжённости. То есть слово «совпадает» связано с тем, что потенциал − это характеристика поля самого по себе, а потенциальная энергия пробного заряда в поле характеризует и поле, и пробный заряд. Иными словами,
![]()
Потенциальная энергия единичного положительного пробного заряда
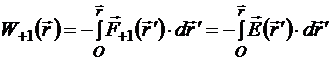 .
.
Тогда по определению потенциала
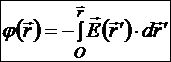 .
.
Эта формула позволяет определить потенциал поля в любой точке пространства по известному полю напряжённости. Здесь точка О выбрана началом отсчёта потенциала (j(О)=0). Значит, потенциальная энергия пробного заряда в поле источников имеет вид:
![]()
Отсюда можно получить физическую размерность потенциала: 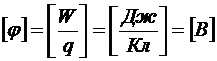 . Потенциал в СИ измеряется в вольтах.
. Потенциал в СИ измеряется в вольтах.
Работа сил поля на перемещении пробного заряда определяется по закону изменения его потенциальной энергии:
![]() Þ
Þ 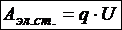 ,
,
где 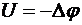 − сброс потенциала или напряжение.
− сброс потенциала или напряжение.
Из формулы связи потенциала и напряжённости 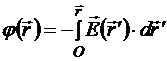 следует формула разности потенциалов:
следует формула разности потенциалов:
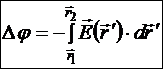
и выражение элементарного изменения или дифференциала потенциала:
![]() .
.
§14.3. Связь между векторным полем напряжённости и скалярным полем потенциала
Очевидно, что распределение в пространстве потенциала данного электростатического поля с точки зрения математики представляет скалярное поле ![]() . Оказывается, последняя формула предыдущего параграфа указывает на то, что векторное поле напряжённости
. Оказывается, последняя формула предыдущего параграфа указывает на то, что векторное поле напряжённости ![]() однозначно определяется заданием скалярного поля потенциала
однозначно определяется заданием скалярного поля потенциала ![]() . Значит, данное электростатическое поле одинаково успешно может быть представлено как векторным полем , так и скалярным полем
. Значит, данное электростатическое поле одинаково успешно может быть представлено как векторным полем , так и скалярным полем ![]() . Покажем это.
. Покажем это.
Используя координатное представление скалярного произведения в декартовых координатах, перепишем выражение элементарного изменения потенциала:
![]() .
.
С другой стороны, поскольку , то дифференциал j в соответствие с правилами дифференцирования функции многих переменных
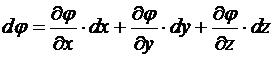 .
.
Сравнивая эти два равенства, приходим к выводу, что
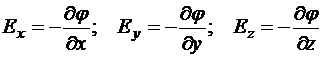
Значит, действительно, задание скалярного поля определяет все его частные производные, а это, оказывается, определяет проекции вектора на координатные оси, что, очевидно, однозначно определяет вектор . Таким образом, поле напряжённости получается в результате процедуры трехмерного дифференцирования поля потенциала. Эта математическая процедура называется градиентом.
В математике процедуру или совокупность действий по преобразованию функции называют оператором. Градиент является многомерным дифференциальным оператором. В трёхмерном случае (случай функции 3-х переменных) градиент обозначается и выражается так:
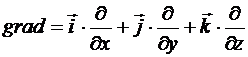 .
.


