Дифракция света
Этот интерферометр сыграл фундаментальную роль в развитии науки и техники. С его помощью впервые была измерена длина световой волны, проведено изучение тонкой структуры спектральных линий, выполнено первое прямое сравнение эталонного метра с определенной длиной волны света. С помощью этого интерферометра был осуществлен знаменитый опыт Майкельсона-Морли, доказавший независимость скорости света от движения Земли.
2.3.5. Рассмотрим теперь прибор, существенная часть которого состоит из двух идентичных плоскопараллельных пластинок толщины h к с показателем преломления n — интерферометр Жамена (рис. 2.9).
При падении пучка света на первую пластинку (на рисунке показан только один луч) часть лучей отразится от передней грани пластинки, а часть, преломившись, отразится от задней грани; таким образом, из пластинки выйдут два выходят два когерентных параллельных луча.
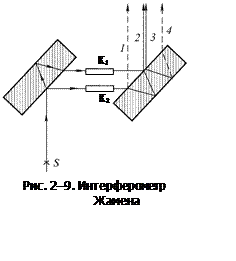 Пройдя сквозь совершенно одинаковые закрытые стеклянные кюветы К1 и К2 (длина кювет l), каждый из лучей, попадая на вторую пластинку, опять раздвоится, и из второй пластинки выйдут уже четыре пучка. Лучи 1 и 4 не попадают в оправу объектива, а лучи 2 и 3 собираются линзой и интерферируют.
Пройдя сквозь совершенно одинаковые закрытые стеклянные кюветы К1 и К2 (длина кювет l), каждый из лучей, попадая на вторую пластинку, опять раздвоится, и из второй пластинки выйдут уже четыре пучка. Лучи 1 и 4 не попадают в оправу объектива, а лучи 2 и 3 собираются линзой и интерферируют.
Полосы интерференции рассматриваются с помощью окуляра, который на рисунке не показан. Если одну из кювет заполнить газом, имеющим известный абсолютный показатель преломления n1, а вторую — газом, показатель преломления n2 которого измеряется, то между интерферирующими лучами возникнет оптическая разность хода, равная ![]() . Соответственно произойдет смещение интерференционной картины на
. Соответственно произойдет смещение интерференционной картины на ![]() полос, причем
полос, причем
![]()
Например, при l=5 см и l=0,5 мкм смещению полос на 0,1 их ширины, которое еще можно зарегистрировать, соответствует очень малое изменение разности (n2— n1):
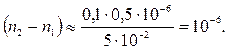
Таким образом, интерферометр Жамена можно использовать для определения ничтожного изменения показателя преломления, например при изменении температуры газа или прибавлении посторонних примесей. В соответствии с этим его нередко называют интерференционным рефрактометром. Как показано выше, он крайне чувствителен к незначительным изменениям показателя преломления. Однако определение абсолютного значения самого показателя преломления при помощи этого прибора довольно затруднительно. Обычно его применяют таким образом, что сравнивают интересующий нас газ с каким-либо хорошо изученным газом, например, воздухом.
3. Дифракция света
3.1. Принцип Гюйгенса — Френеля
Дифракцией называется огибание волнами препятствий, встречающихся на их пути, или в более широком смысле — любое отклонение распространения волн вблизи любых неоднородностей (препятствий) от законов геометрической оптики. Благодаря дифракции волны могут попадать в область геометрической тени, огибать препятствия, проникать через небольшие отверстия в экранах и т. д.
Различают два вида дифракции:
1. Дифракция в непараллельных лучах (дифракция Френеля), когда на препятствие падает сферическая (или плоская) волна, а дифракционная картина наблюдается на экране, находящемся за ним на конечном расстоянии от препятствия.
2. Дифракция в параллельных лучах (дифракция Фраунгофера), когда на препятствие падает плоская волна, а дифракционное изображение источника света наблюдается на экране, расположенном в фокальной плоскости собирающей линзы, установленной на пути прошедшего за препятствие света.
Явление дифракции объясняется с помощью принципа Гюйгенса, согласно которому каждая точка, до которой доходит волна, служит центром вторичных волн, а огибающая этих волн дает положение волнового фронта в следующий момент времени.
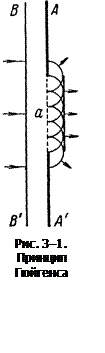 Пусть плоская волна нормально падает на отверстие в непрозрачном экране (рис. 3-1). Согласно Гюйгенсу, каждая точка волнового фронта служит источником вторичных волн (в однородной изотропной среде они сферические). Построив огибающую вторичных волн видим, что волна огибает края отверстия, т. е. фронт волны заходит в область геометрической тени.
Пусть плоская волна нормально падает на отверстие в непрозрачном экране (рис. 3-1). Согласно Гюйгенсу, каждая точка волнового фронта служит источником вторичных волн (в однородной изотропной среде они сферические). Построив огибающую вторичных волн видим, что волна огибает края отверстия, т. е. фронт волны заходит в область геометрической тени.
Принцип Гюйгенса решает задачу о направлении распространения волнового фронта, но не затрагивает вопроса об амплитуде волн, распространяющихся по разным направлениям. Френель вложил в принцип Гюйгенса физический смысл, дополнив его идеей интерференции вторичных волн.
Согласно принципу Гюйгенса — Френеля, световая волна, возбуждаемая каким-либо источником S, может быть представлена как результат суперпозиции когерентных вторичных волн, «излучаемых» фиктивными источниками. Такими источниками могут служить бесконечно малые элементы любой замкнутой поверхности, охватывающей источник S. В качестве этой поверхности выбирают одну из волновых поверхностей, поэтому все фиктивные источники действуют синфазно. Таким образом, волны, распространяющиеся от источника, являются результатом интерференции всех когерентных вторичных волн.
Учет амплитуд и фаз вторичных волн позволяет в каждом конкретном случае найти амплитуду (интенсивность) результирующей волны в любой точке пространства, т. е. определить закономерности распространения света.
3.2. Метод зон Френеля
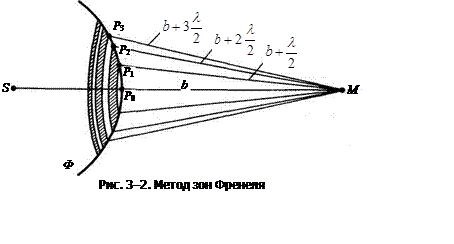
Принцип Гюйгенса является чисто геометрическим способом построения волновых поверхностей. Он никак не связан с физической природой волн и применим как к упругим, так и к электромагнитным волнам в равной мере. Найдем в произвольной точке М амплитуду световой волны, распространяющейся в однородной среде из точечного источника S (рис. 3-2).
Согласно принципу Гюйгенса — Френеля, заменим действие источника S действием воображаемых источников, расположенных на вспомогательной поверхности Ф, являющейся поверхностью фронта волны, идущей из источника S. Френель разбил волновую поверхность Ф на кольцевые зоны такого размера, чтобы расстояния от краев зоны до М отличались на l/2, т. е. Р1М — Р0М=Р2М- Р1М=Р3М — Р2М=…= l/2. Подобное разбиение фронта волны на зоны можно выполнить, проведя с центром в точке М сферы радиусами b+l/2, b+2l/2, b+3l/2, … .
Так как колебания от соседних зон проходят до точки М расстояния, отличающиеся на l/2, то в точку М они приходят в противоположной фазе и при наложении будут взаимно ослаблять друг друга. Поэтому амплитуда результирующего светового колебания в точке М
A=А1- А2+ А3- А4+ … , (3.1)
 |
где А1, А2, … — амплитуды колебаний, возбуждаемых 1-й, 2-й, … зонами.
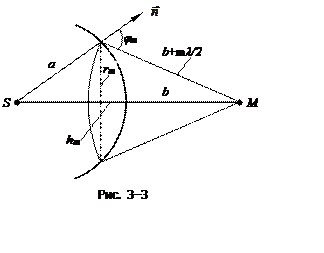
Для оценки амплитуд колебаний найдем площади зон Френеля. Пусть внешняя граница m-й зоны выделяет на волновой поверхности сферический сегмент высоты hm (рис. 3-3). Если площадь этого сегмента sm, то площадь m-й зоны Френеля равна Dsm = sm — sm-1, где sm-1 — площадь сферического сегмента, выделяемого внешней границей (m-1)-й зоны. Из рисунка следует, что
 |
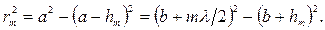 (3-2)
(3-2)
Учитывая, что l<<а и l<<b, получим
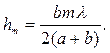 (3-3)
(3-3)
Площадь сферического сегмента и площадь m-й зоны Френеля соответственно равны
![]() (3-4)
(3-4)
Выражение (3-4) не зависит от номера зоны m; следовательно, при не слишком больших m площади зон Френеля одинаковы.
Согласно предположению Френеля, действие отдельных зон в точке М тем меньше, чем больше угол jm (рис. 3-3) между нормалью n к поверхности зоны и направлением на М, т. е. действие зон постепенно убывает от центральной (около Р0) к периферическим (до нуля). Кроме того, интенсивность излучения в направлении точки М уменьшается с ростом номера зоны m и вследствие увеличения расстояния от зоны до точки М. Учитывая оба этих фактора, можем записать
А1> А2> А3> А4 … .
Общее число зон Френеля, умещающихся на полусфере, очень велико; например, при а=b=10 см и l = 0,5 мкм оно равно 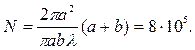
Так как число зон Френеля велико, то в качестве допустимого приближения можно считать, что амплитуда колебания Аm от некоторой m-й зоны Френеля равна среднему арифметическому от амплитуд примыкающих к ней зон, т. е.
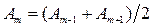 . (3-5)
. (3-5)
Тогда выражение (3-1) можно записать в виде
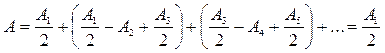 . (3-6)
. (3-6)


