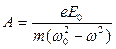| Дисперсия света

Таким образом, скорость света в среде связана с показателем преломления вещества соотношением:

=c/n.

Согласно электромагнитной теории Максвелла абсолютный показатель преломления среды

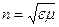где -диэлектрическая проницаемость среды,-магнитная проницаемость. В оптической области спектра для всех прозрачных диэлектриков , поэтому имеем

или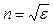

Дисперсия света может быть охарактеризована функцией = () или = (), поскольку длина волны и частота связаны соотношением .

Дисперсией вещества называется величина , определяющая степень растянутости спектра вблизи данной длины волны . Дисперсия называется нормальной, если с ростом длины волны показатель преломления уменьшается, т. е. 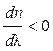и аномальной, если (рис.5-1 и рис.5-3). Для прозрачных веществ характерно монотонное возрастание показателя преломления с уменьшением длины волны (рис. 5-1).

Рис. 5-1. Зависимость показателя преломления среды от длины световой волны и ее частоты в случае нормальной дисперсии.

В своем, ставшим классическим, опыте по разложению белого света Ньютон столкнулся с дисперсией света, еще не подозревая об электромагнитной природе световых волн. Опыт Ньютона состоял в том, что узкий пучок солнечного света он направил на боковую грань трехгранной призмы, а при выходе пучка из противоположной боковой грани наблюдались разноцветные лучи в следующей последовательности – красный(К), оранжевый(О), желтый(Ж), зеленый(З), голубой(Г), синий(С), фиолетовый (Ф) (рис.5-2). Полученную им цветную полоску Ньютон назвал спектром.

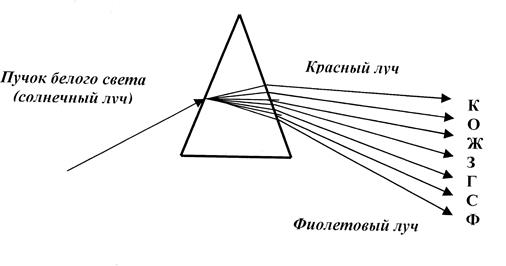
Рис.5-2. Разложение белого света в спектр 3-хгранной призмой.

а

а

(участки " а " )

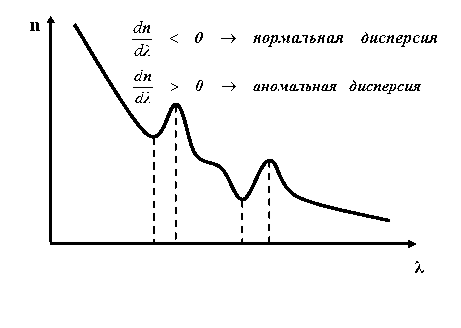
Рис. 5-3. Зависимость показателя преломления среды от длины световой волны в случае нормальной и аномальной дисперсии.

Основы теории дисперсии света могут быть получены, если рассматривать взаимодействие световых волн с электронами атомов. Теоретическому рассмотрению проще всего поддается дисперсия в газах, т. к. в этом случае в первом приближении можно не учитывать сложное взаимодействие атомов и молекул среды. Согласно современным научным представлениям, движение электронов в атоме подчиняется законам квантовой механики, а не классической физики, тем не менее, как показал Лоренц, для качественного понимания многих оптических явлений достаточно ограничится гипотезой о существовании внутри атомов квазиупруго связанных электронов. Электроны, входящие в состав атомов, можно разделить на периферийные, так называемые, оптические, и электроны внутренних оболочек. На излучение и поглощение света в оптическом диапазоне влияние оказывают лишь оптические электроны. Для простоты предположим сначала, что в атоме есть всего один оптический электрон. В классической теории оптический электрон можно рассматривать как затухающий гармонический осциллятор, вынужденные колебания которого происходят под действием переменного поля электромагнитной световой волны и описываются дифференциальным уравнением, представляющим собой уравнение движения электрона:

где m – масса электрона, e – его заряд, k – константа, аналогичная коэффициенту упругости, x – смещение электрона, kx — квазиупругая возвращающая сила, стремящаяся вернуть электрон в положение равновесия, — константа, аналогичная коэффициенту сопротивления при рассмотрении затухающих колебаний, — сила, аналогичная силе трения и формально введенная для учета поглощения света, – напряженность действующего на электрон электрического поля световой волны, имеющей циклическую частоту и амплитуду E0

Уравнения движения электрона можно также переписать в виде:

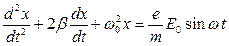
где введены следующие обозначения: и 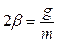— собственная частота осциллятора, — коэффициент затухания.

В предположении, что сила сопротивления незначительна (коэффициент сопротивления =0, что приводит и к = 0), уравнение движения электрона можно упростить и записать его в виде:

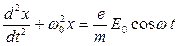
Теория дифференциальных уравнений позволяет найти решение этого уравнения в виде: 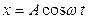, где амплитуда вынужденных колебаний электрона: