Допускаемое напряжение

Допускаемое напряжение – это наибольшее напряжение, при котором обеспечивается требуемая прочность, жёсткость и долговечность элемента конструкции в заданных условиях его эксплуатации.

Допускаемое напряжение составляет некоторую долю от предельного напряжения:

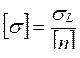, (2.18)

где – нормативный коэффициент запаса, число, показывающее, во сколько раз допускаемое напряжение меньше предельного.

Для пластичных материалов допускаемое напряжение выбирают так, чтобы при любых неточностях расчёта или непредвиденных условиях эксплуатации в материале не возникло остаточных деформаций, т. е. (предел текучести):

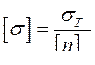, (2.19)

где – коэффициент запаса прочности по отношению к .

Для хрупких материалов допускаемые напряжения назначаются из условия, что материал не разрушится, т. е (предел прочности):

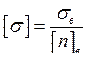, (2.20)

где – коэффициент запаса прочности по отношению к .

В машиностроении (при статическом нагружении) коэффициенты запаса прочности принимают: для пластичных материалов =1,4 – 1,8; для хрупких – =2,5 – 3,0.

Расчёт на прочность по допускаемым напряжениям основан на том, что наибольшее расчётное напряжение в опасном сечении стержневой конструкции не превосходит допускаемого значения (меньше – не более 10 %, больше – не более 5 %):

. (2.21)

Оценка жёсткости стержневой конструкции проводится на основе проверки условия жёсткости при растяжении:

. (2.22)

Величина допускаемой абсолютной деформации [∆l] назначается отдельно для каждой конструкции.

Метод допускаемых нагрузок заключается в том, что внутренние силы, возникающие в наиболее опасном сечении конструкции в процессе эксплуатации, не должны превышать допускаемых значений нагрузок:

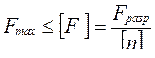, (2.23)

где — разрушающая нагрузка, полученная в результате расчётов или экспериментов с учётом опыта изготовления и эксплуатации;

– коэффициент запаса прочности.

В дальнейшем будем использовать метод допускаемых напряжений и деформаций.

2.6. Проверочный и проектировочный расчёты

на прочность и жёсткость

Условие прочности (2.21) даёт возможность проводить три вида расчетов:

– проверочный – по известным размерам и материалу стержневого элемента (заданы площадь сечения А и [σ]) проверить, в состоянии ли он выдержать заданную нагрузку (N):

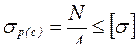; (2.24)

– проектировочный – по известным нагрузкам (N – задано) и материалу элемента, т. е. по известному [σ], подобрать необходимые размеры поперечного сечения, обеспечивающего его безопасную работу:

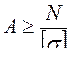; (2.25)

– определение допускаемой внешней нагрузки – по известным размерам (А – задано) и материалу элемента конструкции, т. е. по известному [σ], найти допускаемую величину внешней нагрузки:

. (2.26)

Оценка жёсткости стержневой конструкции проводится на основе проверки условия жёсткости (2.22) и формулы (2.10) при растяжении:

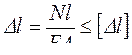. (2.27)

Величина допускаемой абсолютной деформации [∆l] назначается отдельно для каждой конструкции.

Аналогично расчётам по условию прочности условие жёсткости также предполагает три вида расчётов:

– проверка жёсткости данного элемента конструкции, т. е. проверка выполнения условия (2.22);

– расчёт проектируемого стержня, т. е. подбор его поперечного сечения:

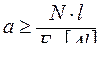; (2.28)

– установка работоспособности данного стержня, т. е. определение допустимой нагрузки:

. (2.29)

Прочностной анализ любой конструкции содержит следующие основные этапы:

1. Определение всех внешних сил и сил реакций опор.

2. Построение графиков (эпюр) силовых факторов, действующих в поперечных сечениях по длине стержня.

3. Построение графиков (эпюр) напряжений вдоль оси конструкции, нахождение максимума напряжений. Проверка условий прочности в местах максимальных значений напряжений.

4. Построение графика (эпюры) деформации стержневой конструкции, нахождение максимумов деформации. Проверка в сечениях условий жёсткости.

Пример 2.1. Для стального стержня, изображённого на рис. 9а, определить во всех поперечных сечениях продольную силу N и напряжение σ. Определить также вертикальные перемещения δ для всех поперечных сечений стержня. Результаты изобразить графически, построив эпюры N, σ и δ. Известно: F1 = 10 кН; F2 = 40 кН; А1 = 1 см2; А2 = 2 см2; l1 = 2 м; l2 = 1 м.

Решение. Для определения N, используя метод РОЗУ, мысленно разрезаем стержень по сечениям I−I и II−II. Из условия равновесия части стержня ниже сечения I−I (рис. 9.б) получим 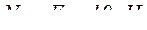(растяжение). Из условия равновесия стержня ниже сечения II−II (рис. 9в) получим

,

откуда (сжатие). Выбрав масштаб, строим эпюру продольных сил (рис. 9г). При этом растягивающую силу считаем положительной, сжимающую − отрицательной.

Напряжения равны: в сечениях нижней части стержня (рис. 9б)

(растяжение);

в сечениях верхней части стержня

(сжатие).

В выбранном масштабе строим эпюру напряжений (рис. 9д).

Для построения эпюры δ определяем перемещения характерных сечений В−В и С−С (перемещение сечения А−А равно нулю).

Сечение В−В будет перемещаться вверх, поскольку верхняя часть сжимается:

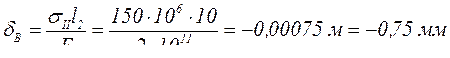(вверх).