Экспериментальное подтверждение гипотезы де-бройля

Полученный результат весьма привлекателен, в частности, велико искушение попытаться интерпретировать материальную частицу как волновой пакет, образованный в результате суперпозиции группы волн. И действительно, на основании соотношения 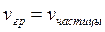в течение некоторого времени частицу было принято считать образованием группы волн де-Бройля. Т. е. полагали, что волны первичны, а частицы представляют собой их образования – волновые пакеты. Однако оказалось, что все не так просто. Эта весьма заманчивая интерпретация наталкивается на непреодолимые трудности.

а) Такого рода волновой пакет, вообще говоря, неустойчив и очень скоро расплывется, т. к. волны де-Бройля испытывают дисперсию в пустоте в силу зависимости фазовой скорости от длины волны, т. е. . В то же время мы знаем, что частицы живут весьма долго.

б) Частица-волна должна испытывать дифракцию. Поэтому с помощью дифракционной решетки можно разложить волновой пакет на составляющие, что снова приведет к уничтожению частицы.

3) Волны де-Бройля и стационарные орбиты.

Согласно постулатам Бора условие квантования круговых орбит: 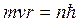. Отсюда получаем 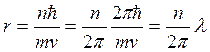, т. е. 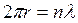. Это означает, что на круговой орбите укладывается целое число волн де-Бройля. Таким образом, имеется красивая интерпретация стационарных состояний – стоячая волна де-Бройля, которая, как известно, энергию не переносит (не излучает).

3. Экспериментальное подтверждение гипотезы де-Бройля.

Ввиду смелости и необычности гипотезы де-Бройля о волновой природе вещества сразу же возникает естественный вопрос: можно ли и если да, то каким именно образом проверить эту гипотезу экспериментально? Понятно, что самое яркое свойство волн – возможность испытывать интерференцию и дифракцию, где наблюдаемой величиной, по сути, является длина волны.

Такие опыты были проведены сначала с электронами, а затем с нейтронами и атомами.

Сделаем некоторые оценки, позволяющие определить порядок длин волн с которым мы встретимся, имея дело с электронными пучками.

Рассмотрим сначала нерелятивистский случай.

Пусть электроны, ускоряемые электрическим полем, проходят разность потенциалов . Тогда скорость электрона находим из условия 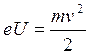, а его импульс: . Длина волны де-Бройля такого электрона равна 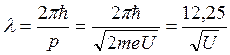, если длина волны измеряется в ангстремах, а напряжение – в вольтах. Оценки показывают, что при ускоряющих напряжениях от единиц вольт до киловольт де-бройлевская длина волны электрона приблизительно такая же, как у мягкого рентгеновского излучения. При длина волны электрона соответствует уже жесткому рентгену. Т. о., для наблюдения дифракции электронов, как и в случае рентгеновских лучей, можно использовать решетку кристалла.

Примечание.

Учитывать релятивистский характер движения электронов необходимо, начиная со значений ускоряющих напряжений .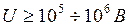

;

.

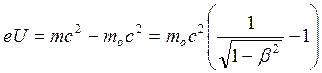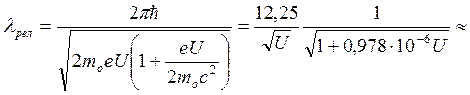
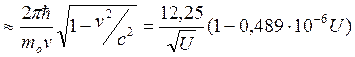Де-бройлевские длины волн электрона для различных ускоряющих напряжений приведены в таблице.

1 10 102 103 4.104 105 106

12,25 3,9 1,22 0,39 0,061 0,039 0,012

0,059 0,037 0,008

1)  Опыты Дэвиссона и Джермера.

В 1927 г. К. Дэвиссон (1881-1958 гг.) и Л. Джермер (1896-1971 гг.) [Davisson C. J., Germer L. H., Diffraction of Electrons by a Crystal of Nickel, Phys. Rev. 30, 705 (1927)] исследовали отражение электронов от монокристалла никеля.

Опыты, приведшие к открытию дифракции электронов были начаты Дэвиссоном ещё в 1919 г. Однако первые результаты не увязывались с наличием волновых свойств у микрочастиц.

На то, что электроны, обладающие подобно пучкам света волновыми

свойствами, рассеиваясь на подходящей решетке, должны дать

дифракционную картину, первым обратил внимание Элзассер в 1925 г.

Решетка кристалла “работает” аналогично дифракционной решетке:

отраженные от кристаллических плоскостей волны материи образуют

в результате суперпозиции дифракционную картину точно также, как

вторичные волны от щелей дифракционной решетки.

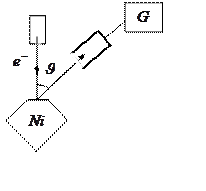
В своем историческом опыте Дэвиссон и Джермер использовали

метод Брэгга: узкий пучок электронов, имеющих одинаковую

скорость (моноэнергетических), направлялся на поверхность

монокристалла никеля, обладающего кубической симметрией.

Кристалл был сошлифован вдоль кристаллографической плоскости

с миллеровскими индексами (111), т. е. перпендикулярно большой

диагонали кристаллической ячейки.

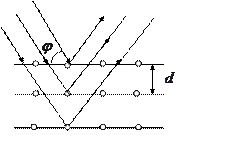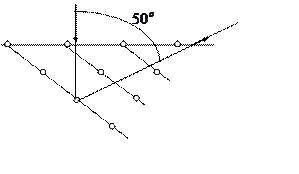Отраженные электроны улавливались цилиндрическим электродом, соединенным с гальванометром. Интенсивность отраженного пучка оценивалась по силе тока, текущего через гальванометр. При нормальном к поверхности кристалла падении пучка максимум интенсивности наблюдался под углом , наиболее значительный при .

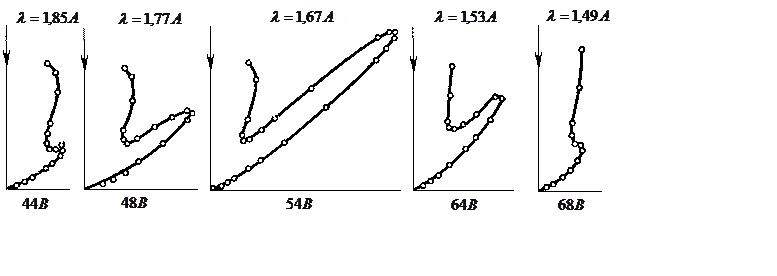На диаграммах приведена зависимость интенсивности отраженного пучка от угла отражения для различных значений ускоряющего напряжения. Вертикальная ось определяет направление падающего пучка. Сила тока в гальванометре пропорциональна длине отрезка, проведенного из начала координат до пересечения с кривой.

Если кристалл рассматривать как совокупность параллельных атомных плоскостей, отстоящих друг от друга на расстоянии , то дифракцию можно рассматривать как результат отражения пучка от системы таких плоскостей. Положение максимумов интенсивности (дифракционных максимумов) определяется условием Брэгга-Вульфа:

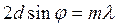(*) , где угол скольжения; 1, 2, 3,…

Так как 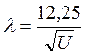, то, подставляя в (*), получаем , .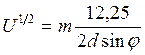